二叉树基础
前言
个人认为Trie比较简单，所以主要就‘笔记’一下二叉树。
1、二叉树的定义
二叉树(Binary Tree) 是由n个结点构成的有限集(n≥0)，n=0时为空树，n>0时为非空树。对于非空树T TT：
-
有且仅有一个根结点；
-
除根结点外的其余结点又可分为两个不相交的子集Tl和Tr，分别称为T的左子树和右子树。且Tl和Tr本身又都是二叉树。
很明显该定义属于递归定义，所以有关二叉树的操作使用递归往往更容易理解和实现。
从定义也可以看出二叉树与一般树的区别主要是两点，一是每个结点的度最多为2；二是结点的子树有左右之分，不能随意调换，调换后又是一棵新的二叉树。
从定义也可以看出二叉树与一般树的区别主要是两点，一是每个结点的度最多为2；二是结点的子树有左右之分，不能随意调换，调换后又是一棵新的二叉树。
2、二叉树的形态
五种基本形态
从上面二叉树的递归定义可以看出，二叉树或为空，或为一个根结点加上两棵左右子树，因为两棵左右子树也是二叉树也可以为空，所以二叉树有5种基本形态：
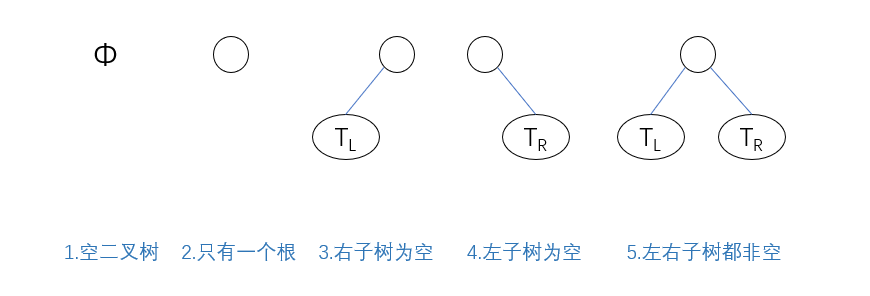
三种特殊形态
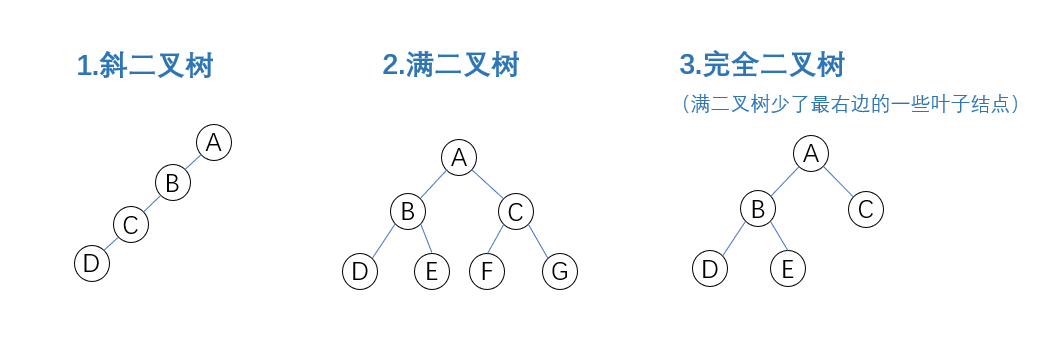
3.二叉树的基本性质
-
在二叉树的第 i 层上最多有 \(2^{i-1}\) 个结点（i 为正整数）
-
深度为 k 的二叉树最多有 \(2^{k-1}\) 个结点（k 为正整数）
-
对任一一棵二叉树，如果其叶结点为 n0，度为2的结点数为 n2，则一定满足：n0=n2+1
-
具有 n 个结点的完全二叉树的深度为 \(floor(log2^n)+1\)
-
如果有一棵有 n 个结点的完全二叉树(其深度为 [log2n] + 1，向下取整)的结点按层次序编号(从第 1 层到第 [log2n] + 1，向下取整层，每层从左到右)，则对任一结点 i（1 <= i <= n）有
1.如果 i = 1，则结点 i 是二叉树的根，无双亲；如果 i > 1，则其双亲是结点 [i / 2]，向下取整
2.如果 2i > n 则结点 i 无左孩子，否则其左孩子是结点 2i
3.如果 2i + 1 > n 则结点无右孩子，否则其右孩子是结点 2i + 1
4.树的结构
在 C 语言中，树的实现和链表的实现有些类似。都是数据区加上指针区。一个典型的树的声明如下：
struct node {
int data;
struct node *left;
struct node *right;
}
typedef struct node node_t;
typedef struct node* nodeptr_t;
一般情况下，如果某一个节点的子节点不存在，我们就使用 NULL 来标记。
5.树的遍历
树的遍历操作有三种，前序遍历，中序遍历和后序遍历。三者的不同之处在于处理子节点的时间不同。前序遍历是先处理根节点，然后处理左孩子最后处理右孩子。将处理根节点的操作挪到处理左右节点的操作之间，我们就得到了中序遍历。如果挪到最后，那就是后序遍历。示例如下：
void PrintTree_PreOrder(nodeptr_t root) {
if(root) {
printf("%d\n",root->data);
PrintTree_PreOrder(root->left);
PrintTree_PreOrder(root->right);
}
}
可以看到，我们在遍历树时多次应用了递归。这是由于树的递归定义决定的特点。下面再给出一个遍历的例子：
int treeSize(nodeptr_t root) {
if(root == 0) {
return 0;
}
return 1 + treeSize(root->left) + treesize(root->right)
}
6.二叉树的查找
nodeptr_t treeSearch(nodeptr_t root, int value) {
if(root == NULL)
return NULL;
else if(root->data == value)
return root;
else if(root->data > target)
return treeSearch(root->left);
else
return treeSearch(root->right);
}
为了防止爆栈这种悲剧发生（概率很低），我们还可以写出迭代版本的搜索算法。示例如下：
nodeptr_t treeSearch(nodeptr_t root, int value)
{
while(root != NULL && root->data != value) {
if(root->data > value) {
root = root->left;
} else {
root = root->right;
}
}
return root;
}
为了处理其他类型的数据，我们还可以把比较操作那里使用函数进行替代。比如我们在实现字典的查找时，就可以简单地使用 strcmp 函数进行比较操作。
7.插入新结点
void treeInsert(nodeptr_t root, int data)
{
nodeptr_t newNode;
newNode = malloc(sizeof(*newNode));
assert(newNode);
newNode->data = data;
newNode->left = 0;
newNode->right = 0;
for(;;) {
if(root->data > data) {
if(root->left) {
root = root->left;
} else {
root->left = newNode;
return;
}
} else {
if(root->right) {
root = root->right;
} else {
root->right = newNode;
return;
}
}
}
}
这种操作的实现是极其简洁的。但是其缺点也是很明显的：这钟插入操作没有尝试平衡树。也就是说，在最坏的情况下，树可能只向某一个方向生长，使之退化为链表。我们会在后面引入改进的树结构来解决问题。
8.删除结点
void treeDelete(nodeptr_t root, int value) {
nodeptr_t temp;
if(root == NULL)
return;
else if(value < root->data)
treeDelete(root->left,data);
else if(value > root->data)
treeDelete(root->right,data);
else if(root->left && root->right) {
temp = __findMin(root->right);
root->data = temp->data;
treeDelete(root->right,root->data);
} else {
temp = root;
if(root->left == NULL)
root = root->right;
else if(root->right == NULL)
root = root->left;
free(temp);
}
}
nodeptr_t __findMin(nodeptr_t root) {
if(root == NULL)
return NULL;
else if(root->left == NULL)
return root;
else
return __findMin(root->left);
}
