Leetcode刷题模版总结
1. 双指针
双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多
个数组的多个指针。
1）滑动窗口
若两个指针指向同一数组，遍历方向相同且不会相交，则也称为滑动窗口（两个指针包围的
区域即为当前的窗口），经常用于区间搜索。
例题：
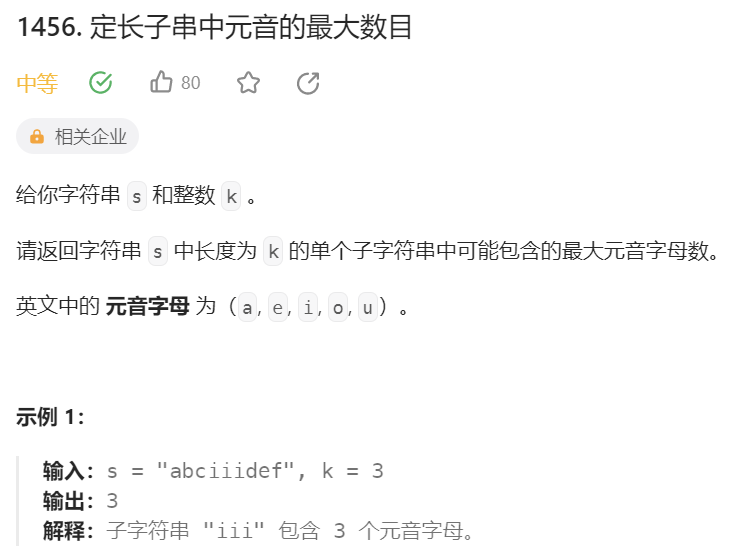
class Solution { public: int maxVowels(string s, int k) { int ans{0}; int count{0}; int l{0}; int r = k - 1; string vowels{"aeiou"}; for (int i = 0; i < k; ++i) { if (vowels.find(s[i]) != string::npos) { count++; } } ans = count; while (r < s.size() - 1) { r++; l++; if (vowels.find(s[r]) != string::npos) { count++; } if (vowels.find(s[l - 1]) != string::npos) { count--; } ans = max(ans, count); } return ans; } };
2）双指针
若两个指针指向同一数组，但是遍历方向相反，则可以用来进行搜索，待搜索的数组往往是
排好序的。
例题：
class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { int left = 0; int right = numbers.size() - 1; while (left < right) { int sum{numbers[left] + numbers[right]}; if (sum == target) { break; } if (sum > target) { right--; } else { left++; } } return vector<int> {left+1, right+1}; } };
2. 二分法
采用左闭右开的写法，
- left和right最初的取值：left = mid + 1， right = mid
- left和right索引时的偏移：left = mid + 1， right = mid
- while里的循环条件：left < right
- mid的取值：mid = left + (right - left) / 2
例题：
class Solution { public: vector<int> searchRange(vector<int>& nums, int target) { vector<int> ans{-1, -1}; if (nums.empty()) { return ans; } int lowerBound = binsearchLower(nums, target); int upperBound = max(0, binsearchUpper(nums, target) - 1); ans = {lowerBound, upperBound}; if ((lowerBound > nums.size()) || (nums[upperBound] != target)) { ans = {-1, -1}; return ans; } return ans; } int binsearchLower(const vector<int>& nums, int target) { int l = 0; int r = nums.size(); int mid{0}; while (l < r) { mid = int(l + (r - l) / 2); if (nums[mid] >= target) { r = mid; } else { l = mid + 1; } } return l; } int binsearchUpper(const vector<int>& nums, int target) { int l = 0; int r = nums.size(); int mid{0}; while (l < r) { mid = int(l + (r - l) / 2); if (nums[mid] > target) { r = mid; } else { l = mid + 1; } } return l; } };
3. DFS深度优先搜索
一般来说，深度优先搜索类型的题可以用递归或者栈来实现，用递归写法比较好写，里面会用到主函数和辅函数，
主函数用于遍历所有的搜索位置，判断是否可以开始搜索，如果可以即在辅函数进行搜索。
辅函数则负责深度优先搜索的递归调用
例题：
class Solution { public: // 辅函数 int LandDFS(vector<vector<int>>& grid, int i, int j) { // 在矩阵尺寸范围内 if((i < grid.size()) && (i >= 0) && (j < grid[0].size()) && (j >= 0)) { if (grid[i][j] == 0) { // 碰到水 return 0; } else { grid[i][j] = 0; return 1 + LandDFS(grid, i-1, j) + LandDFS(grid, i+1, j) + LandDFS(grid, i, j-1) + LandDFS(grid, i, j+1); } } else { return 0; } } // 主函数 int maxAreaOfIsland(vector<vector<int>>& grid) { int ans = 0; for (int i = 0; i < grid.size(); i++) { for (int j = 0; j < grid[0].size(); j++) { ans = max(ans, LandDFS(grid, i, j)); // 这里LandDFS(grid, i, j)返回的是含(i,j)的岛屿的面积 } } return ans; } };
4. BFS广度优先搜索
搜索的题目优先用DFS，因为好写。只有碰到 1) 层序遍历，2) 最短路径 的题时才用BFS。
BFS使用队列，把每个还没有搜索到的点依次放入队列，然后再弹出队列的头部元素当做当前遍历点。BFS总共有两个模板：
模板1：如果不需要确定当前遍历到了哪一层，BFS模板如下。
1 while queue 不空：
2 cur = queue.pop() // 弹出队列的头部元素当做当前遍历点
3 for 节点 in cur的所有相邻节点：
4 if 该节点有效且未访问过：
5 queue.push(该节点)
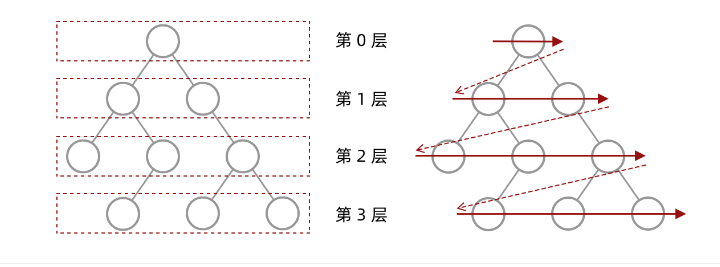
模板2：如果要确定当前遍历到了哪一层，BFS模板如下。
这里增加了level表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size表示在当前遍历层有多少个元素，也就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。
level = 0
while queue 不空：
{
size = queue.size() // size表示即将要遍历的那一层的元素个数。
while (size --) // 当size减到0时，代表这一层遍历完了
{
cur = queue.pop()
for 节点 in cur的所有相邻节点：
if 该节点有效且未被访问过：
queue.push(该节点)
}
level ++;
}
上面两个是通用模板，在任何题目中都可以用，是要记住的！
例题：
LeetCode 102. Binary Tree Level Order Traversal 二叉树的层序遍历（Medium）
本题要求二叉树的层次遍历，所以同一层的节点应该放在一起，故使用模板二。
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> res; queue<TreeNode*> que; que.push(root); if (root ==nullptr) { return res; } while (!que.empty()) { int size = que.size(); vector<int> temp; while (size--) { TreeNode* cur = que.front(); que.pop(); temp.push_back(cur->val); if (cur->left) { que.push(cur->left); } if (cur->right) { que.push(cur->right); } } // 遍历完一层了 res.push_back(temp); } return res; } };
5. 回溯
回溯法（backtracking）是优先搜索的一种特殊情况，又称为试探法，常用于需要记录节点状
态的深度优先搜索。通常来说，排列、组合、选择类问题使用回溯法比较方便。
解题套路：
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
例题：
class Solution { public: vector<vector<int>> permute(vector<int>& nums) { vector<vector<int>> ans; backtrack(nums, 0, ans); return ans; } void backtrack(vector<int>& nums, int depth, vector<vector<int>>& ans) { if (depth == nums.size() - 1) { ans.push_back(nums); return; } for (int i = depth; i < nums.size(); ++i) { // 修改当前节点状态 swap(nums[i], nums[depth]); // 当前数字nums[i]要和后面所有的数字都要交换一遍（包括他自己） // 递归子节点 backtrack(nums, depth + 1, ans); // 回改当前节点状态 swap(nums[i], nums[depth]); } } };
