特征值问题——polynomial filtering 技术

介绍

为什么会有polynomial呢？因为特征值求解的常用技术比如幂迭代等，会用到polynomial，这些多项式迭代可以写成这种形式，，q代表polynomial的度数。我们因此需要一些近似（approximation）技巧构造一个好的多项式$p_q$。

Filtering方法的用处：增加收敛性，从而达到加速的效果。

Filtering方法的思路：目的是通过预处理近似特征向量或子空间，以增强基本的投影方法（如Arnoldi、Lanczos及子空间迭代）。将这些向量和子空间分为“wanted”部分和“unwanted”部分，减少“unwanted”的部分。

 

例子

设有一个Hermitian矩阵A，其拥有特征值：$\lambda_1>\lambda_2 \geq \cdots \geq \lambda_n$

对应的特征向量为u1, ... , $u_n$.如果我们只对最大特征值$\lambda_1$感兴趣，我们可以使用幂迭代方法，也就是说选择$p_q(t)=t^q$。

能不能选择更好的多项式，来加速它的收敛呢？

设有如下迭代公式:

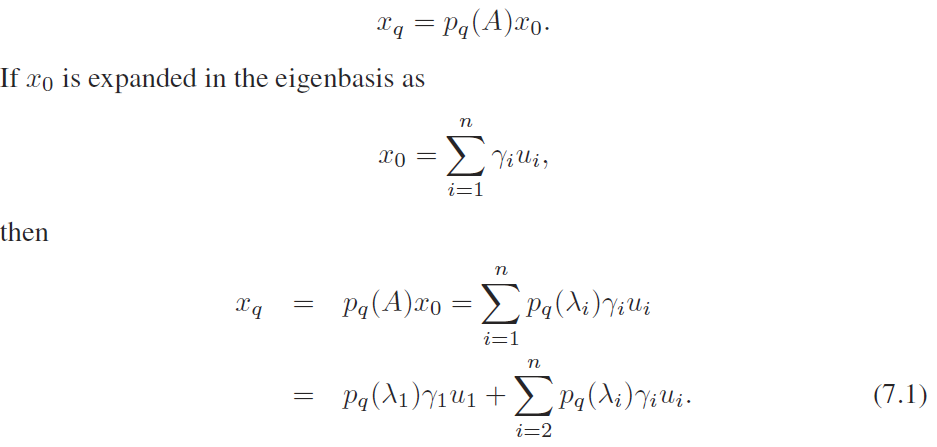
 如果我们只想要第一个特征对（eigenpair），我们则需要（7.1）中的$p_q(\lambda_1)\gamma_1$组分远远大于其它的组分。我们需要寻找一个多项式$p_q$，它在$\lambda_1$处的值为1，在包含所有其它特征值的区间[$\alpha$, $\beta$]中的值越小越好。可以用以下数学公式描述：

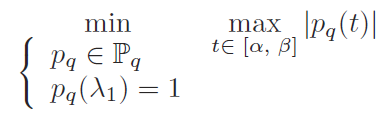
 这个问题的答案就是Chebyshev多项式，依据就是如下定理：

 

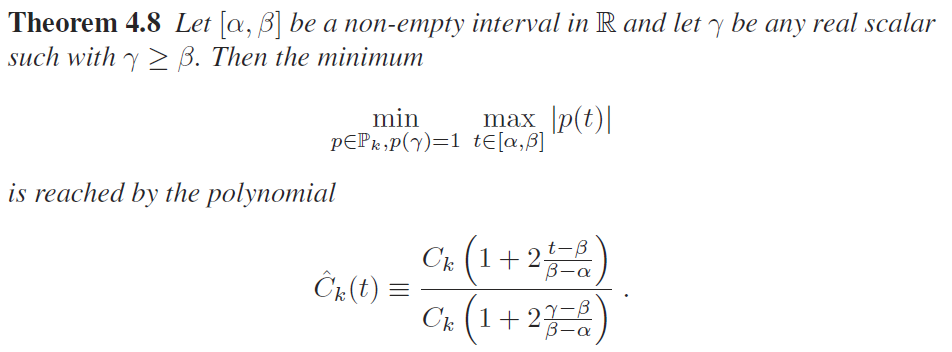
 又由于Chebyshev有著名的3-term recurrence关系：

 所以我们可以写出迭代公式来更新$x_q$：