吃透单调栈（2）——解两道Hard题：接雨水、柱状图中最大的矩形问题

怎么想到要用单调栈的？

这类题目的数据通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置（寻找边界），此时我们就要想到可以用单调栈了。

 

42. 接雨水

这道题就是要求解每一个柱子左边第一个比它高的柱子，以及右边第一个比它高的柱子，然后这两个柱子间形成的凹槽面积。

注意，是横向扫来求面积。比如下图，4号柱左边第一个比它高的柱子是3号，右边第一个比它高的是7号，面积是蓝色框（遍历到7号柱时才会计算面积）。

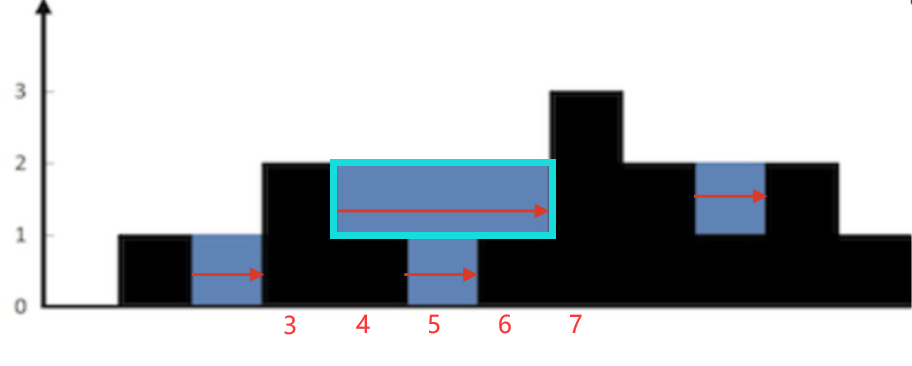
我们额外用一个栈来存储左边第一个更高柱子的编号（为什么是左边，因为用for循环遍历是从左边开始的，左边代表遍历过了的信息）。

右边第一个更高的柱子会出现在for循环遍历时，见下面的case 3。

 在用for循环遍历每一跟柱子时，会出现以下三种情况，我们要根据不同情况来选择如何操作栈。

• case 1：当前遍历的元素（柱子）高度小于栈顶元素的高度 height[i] < height[st.top()]
• case 2：当前遍历的元素（柱子）高度等于栈顶元素的高度 height[i] == height[st.top()]
• case 3：当前遍历的元素（柱子）高度大于栈顶元素的高度 height[i] > height[st.top()]   （碰到了右边第一个更高的柱子）

 

    int trap(vector<int> &height)
    {
        int ans{0};
        stack<int> stk; // 单调递增栈

        for (int i = 0; i < height.size(); ++i)
        {
            while (!stk.empty() && height[i] > height[stk.top()]) // case 3
            {
                int right = i;
                int mid = stk.top();
                stk.pop();
                if (!stk.empty())
                {
                    int left = stk.top(); // 弹出mid后，栈顶元素就是mid左侧第一个比它高的柱子
                    // 计算面积
                    int width = right - left - 1;
                    int h = min(height[left], height[right]) - height[mid];
                    ans += width * h;
                }
            }
            // case 1&2
            stk.push(i);
        }
        return ans;
    }

 

84. 柱状图中最大的矩形

42. 接雨水 是找每个柱子左右两边第一个大于该柱子高度的柱子，而本题是找每个柱子左右两边第一个小于该柱子的柱子。

因此与接雨水相反，该题使用单调递增栈。

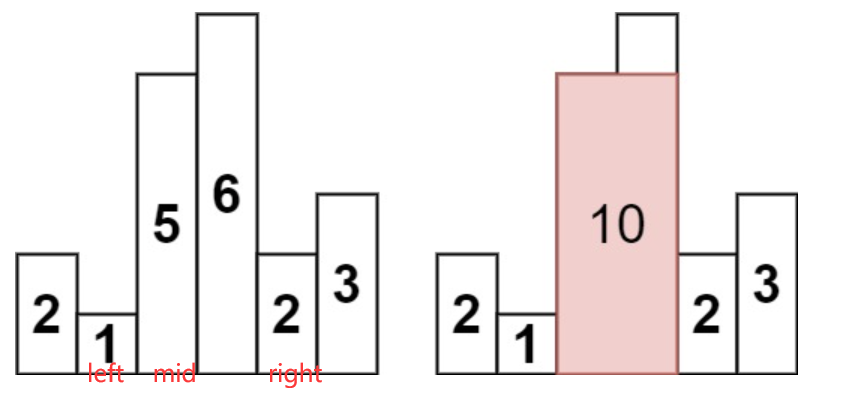
如下图，在2号柱（value: 5）柱左边第一个更小的柱子是1号柱（value: 1），右边第一个更小的柱子是4号柱（value: 2）。意味着以5为高度能贯穿两个边界这之间的柱子。

 

    int largestRectangleArea(vector<int> &heights)
    {
        stack<int> stk; // 单调递减栈
        int ans{0};
        heights.insert(heights.begin(), 0);  // 数组头部加入元素0
        heights.push_back(0);  // 数组尾部加入元素0
        for (int i = 0; i < heights.size(); ++i)
        {
            while (!stk.empty() && heights[i] < heights[stk.top()])
            {
                int right = i;
                int mid = stk.top();
                stk.pop();

                int left = stk.top();
                int width = right - left - 1;
                int h = heights[mid];
                ans = max(ans, width * h);
            }
            stk.push(i);
        }
        return ans;
    }