COMSOL中的求解器(1)—— 方程形式
1. 流程
COMSOL中将PDE转成ODE(瞬态仿真),再通过对时间项离散,最后获得稀疏矩阵方程,通过求解器求解。而稳态仿真则跳过上述时间离散的过程,其余与瞬态仿真求解一致。
流程如下:
瞬态:

稳态:

2. 隐式ODE,及其离散形式

其中,D:质量矩阵;K:刚度矩阵;L{Ω}:载荷;L{partial_Ω}:边界载荷。
将隐式方程L(U对时间的导数, U, t) = 0 进行离散,获得代数系统(代数方程)。
时间离散默认使用后向差分法BDF(隐式欧拉法),其稳定性好。COMSOL会根据精度,自动在1阶到5阶中选择,下图中的G中的q即代表阶数。

3. 非线性求解(牛顿法)
如果物性参数具有非线性,比如随温度变化。那么需要求解的就是一个非线性问题,要用牛顿法求解。
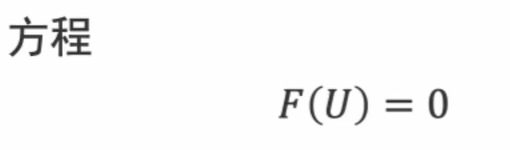
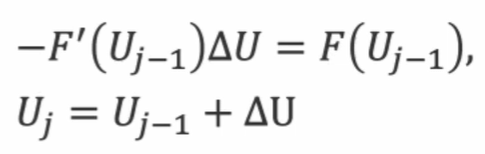
F’是标量形式,矢量形式为Jacobian矩阵。
然而牛顿法的求解是否成功,与初始值的选取有关。若初始值没选正确,会导致迭代时发散。因此,COMSOL中可以选择带阻尼的牛顿法求解。

在COMSOL中可以选择constant 阻尼系数,也可以自动选择阻尼系数。
另外,Jacobian矩阵的更新会很耗时,因此默认使用最少次数更新Jacobian矩阵。如果遇到不收敛,可以手动调整为每次迭代都更新Jacobian矩阵。

下面是非线性求解器设置的技巧:
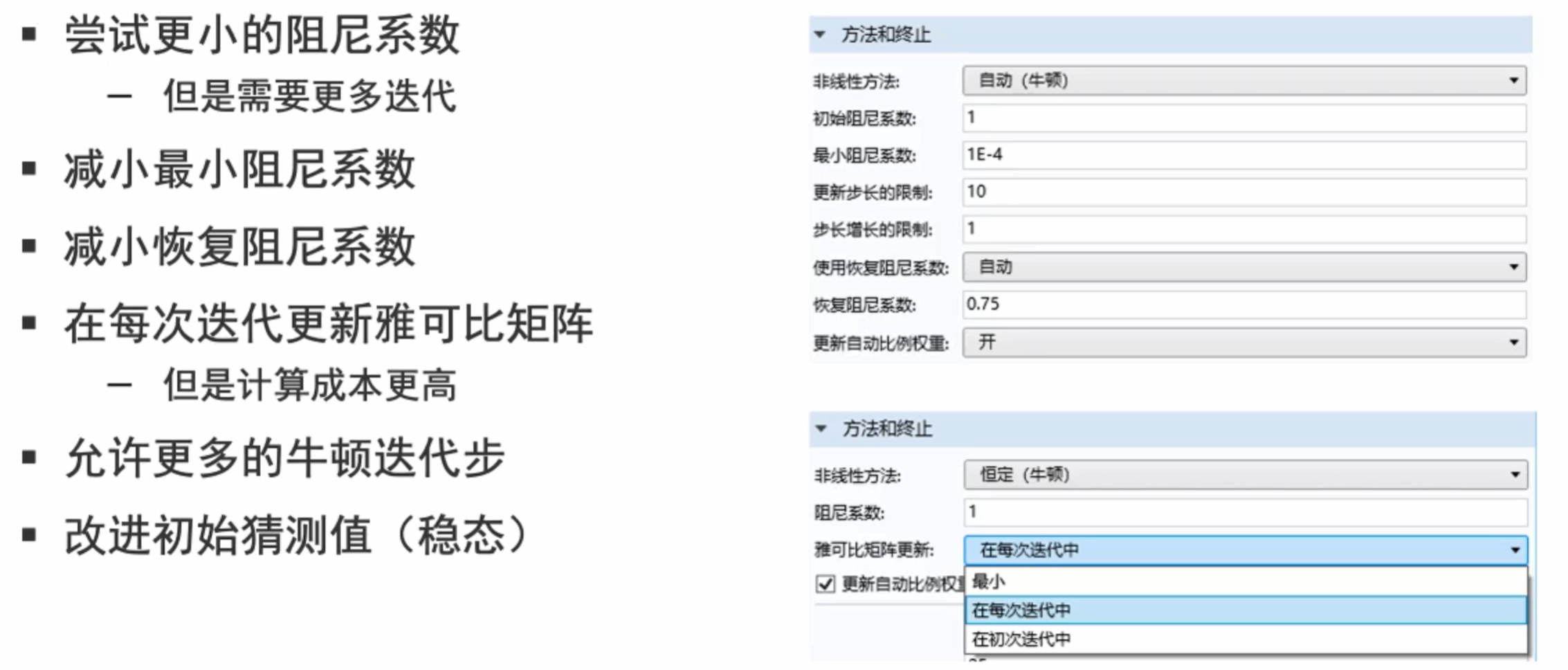
4. 瞬态及稳态的方程小结




