指数积分方法(Exponential Integration)求解ODE/DAE问题
1. 简介
We can classify an integration method by its stability and computational effort. The y-axis represents the stability and x-axis represents the computational effort.
The backward euler is located at top-right corner due to the high stability and also high computational effort of solving a linear system. On the other hand, the forward euler is located at bottom-left corner. There are many previous works for improving either the stability of the explicit method or the performance of the implicit method. Dong and Li propose to use telescopic scheme to improve the stability of the forward euler method. Devgan and Rohrer use adaptive slope control to relax the stability constraints. For the implicit method, Li and Shi re-formulate the backward euler and avoid solving a linear system when the step size is changed.
We devise a method that has acheieved high stability so that the step size will not be limited, and requires only low computational effort. We borrow the concept of exponential time diffferencing in the numerical community, and propose the matrix exponential method.
2. Matrix exponential method (MEXP)
解如下形式的方程，
通过指数积分方法，获得从t到t+h时间的递进关系：
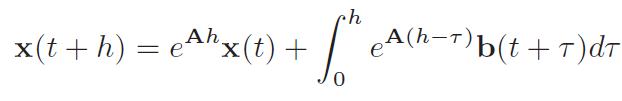
写为如下的矩阵指数形式：
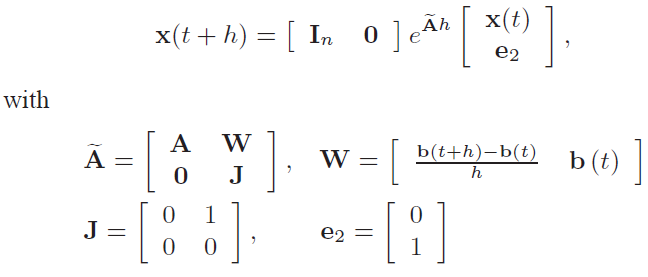
其中，
3. Krylov方法近似
其中的矩阵向量积（MEVP）可以通过Krylov方法近似计算：
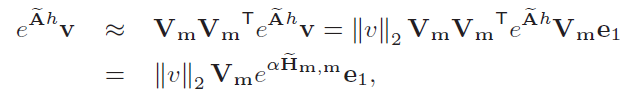
其中Vm是
的Krylov子空间的基。
若C为奇异矩阵，则无法求逆。在实际计算中，我们用
的Krylov子空间基代替，他们求得的Vm是相等的。
其中，
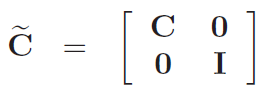
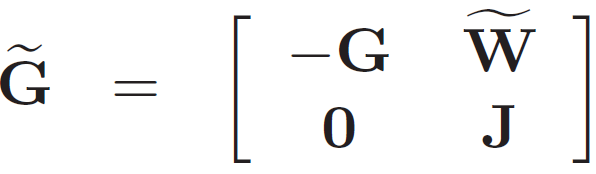
在实际计算中，我们仅用一次LU分解，从而避免后续solve时的重复运算。
其中，
