Krylov子空间与Arnoldi过程

一、应用背景

Krylov 子空间方法就是在Krylov子空间中寻找近似解。

 

二、Krylov子空间

 n是原始矩阵的维度，m为降阶后矩阵的维度，通常m<<n。

 

三、Arnoldi 过程: 计算Km 的一组正交

 

 

对应上述MGS过程的python代码：

import numpy as np

def arnoldi_iteration(A, b, n: int):
    """Compute a basis of the (n + 1)-Krylov subspace of the matrix A.

    This is the space spanned by the vectors {b, Ab, ..., A^n b}.

    Parameters
    ----------
    A : array_like
        An m × m array.
    b : array_like
        Initial vector (length m).
    n : int
        One less than the dimension of the Krylov subspace, or equivalently the *degree* of the Krylov space. Must be >= 1.
    
    Returns
    -------
    Q : numpy.array
        An m x (n + 1) array, where the columns are an orthonormal basis of the Krylov subspace.
    h : numpy.array
        An (n + 1) x n array. A on basis Q. It is upper Hessenberg.
    """
    eps = 1e-12
    h = np.zeros((n + 1, n))
    Q = np.zeros((A.shape[0], n + 1))
    # Normalize the input vector
    Q[:, 0] = b / np.linalg.norm(b, 2)  # Use it as the first Krylov vector
    for k in range(1, n + 1):
        v = np.dot(A, Q[:, k - 1])  # Generate a new candidate vector
        for j in range(k):  # Subtract the projections on previous vectors
            h[j, k - 1] = np.dot(Q[:, j].conj(), v)
            v = v - h[j, k - 1] * Q[:, j]
        h[k, k - 1] = np.linalg.norm(v, 2)
        if h[k, k - 1] > eps:  # Add the produced vector to the list, unless
            Q[:, k] = v / h[k, k - 1]
        else:  # If that happens, stop iterating.
            return Q, h
    return Q, h

　

四、重要性质

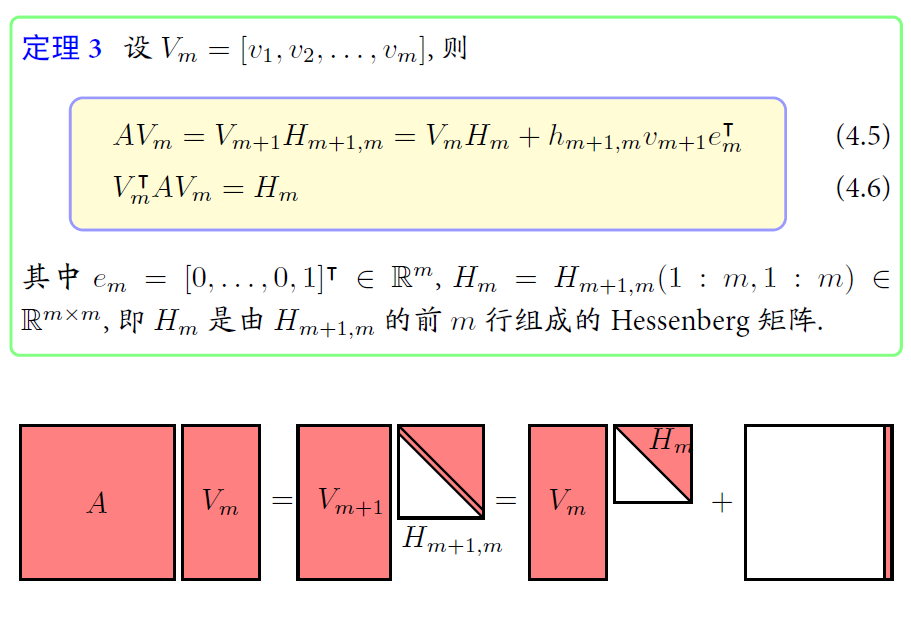
 （4.5）和（4.6）这两个式子在指数积分方法（krylov法）中会有应用。