Delaunay三角剖分——BW算法

Delaunay 三角剖分

定义

在数学和计算几何中，对于给定的平面中的离散点集P ，其 Delaunay 三角剖分 DT() 满足：

  1. 空圆性：DT(P) 是 唯一 的（任意四点不能共圆），在 DT(P) 中，任意 三角形的外接圆范围内不会有其它点存在。
  2. 最大化最小角：在点集P 可能形成的三角剖分中，DT(P) 所形成的三角形的最小角最大。从这个意义上讲，DT(P) 是 最接近于规则化 的三角剖分。具体的说是在两个相邻的三角形构成凸四边形的对角线，在相互交换后，两个内角的最小角不再增大。

一个显示了外接圆的 Delaunay 三角剖分

性质

  1. 最接近：以最接近的三点形成三角形，且各线段（三角形的边）皆不相交。
  2. 唯一性：不论从区域何处开始构建，最终都将得到一致的结果（点集中任意四点不能共圆）。
  3. 最优性：任意两个相邻三角形构成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小角度不会变化。
  4. 最规则：如果将三角剖分中的每个三角形的最小角进行升序排列，则 Delaunay 三角剖分的排列得到的数值最大。
  5. 区域性：新增、删除、移动某一个顶点只会影响邻近的三角形。
  6. 具有凸边形的外壳：三角剖分最外层的边界形成一个凸多边形的外壳。

 

BW算法

简介

Bowyer-Watson算法是一种增量算法。它的工作原理是将点一次一个地，添加到所有点的子集的Delaunay三角剖分中。每次插入新点后，任何外接圆包含新点的三角形都被删除，留下一个星形多边形孔，然后使用新点重新三角化。

 

首先：insert a node in an enclosing "super"-triangle

 

 

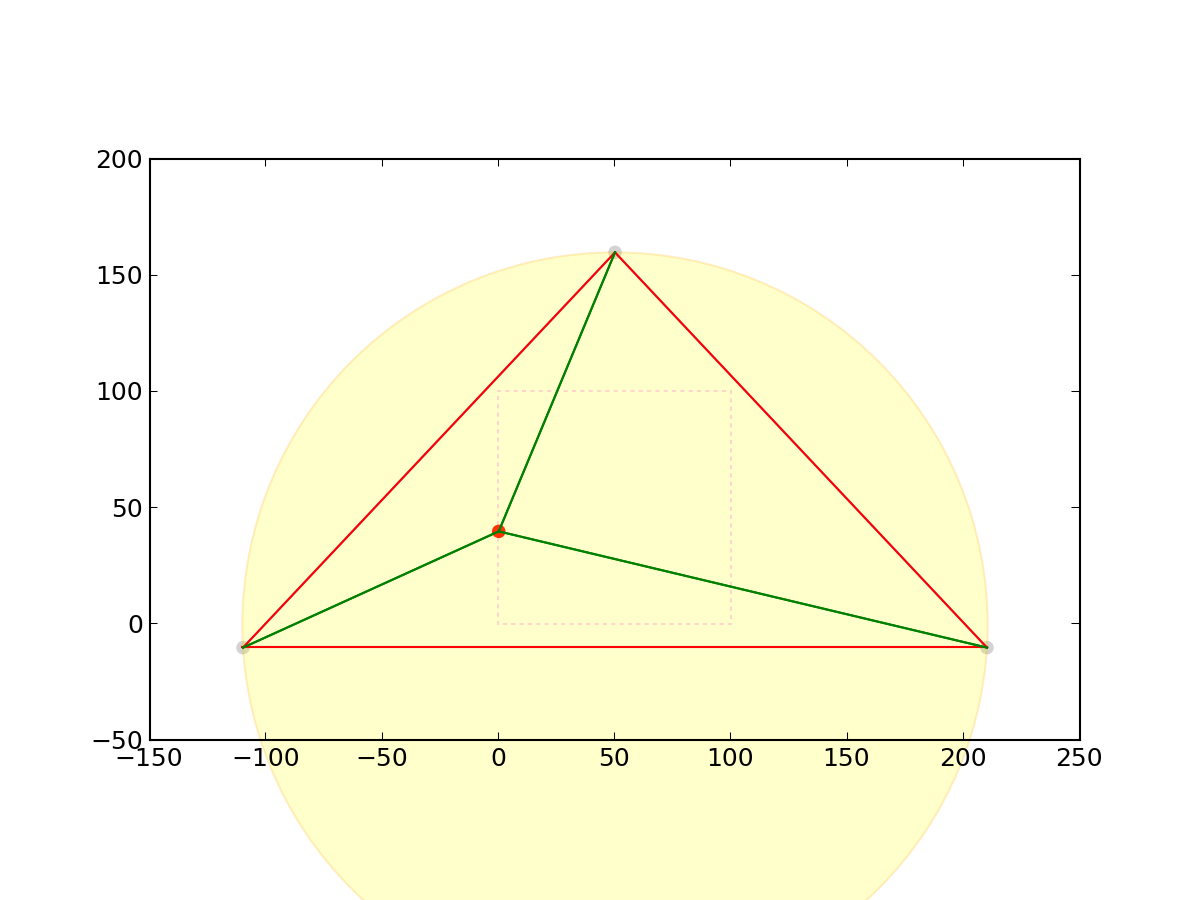
Insert second node

 

 

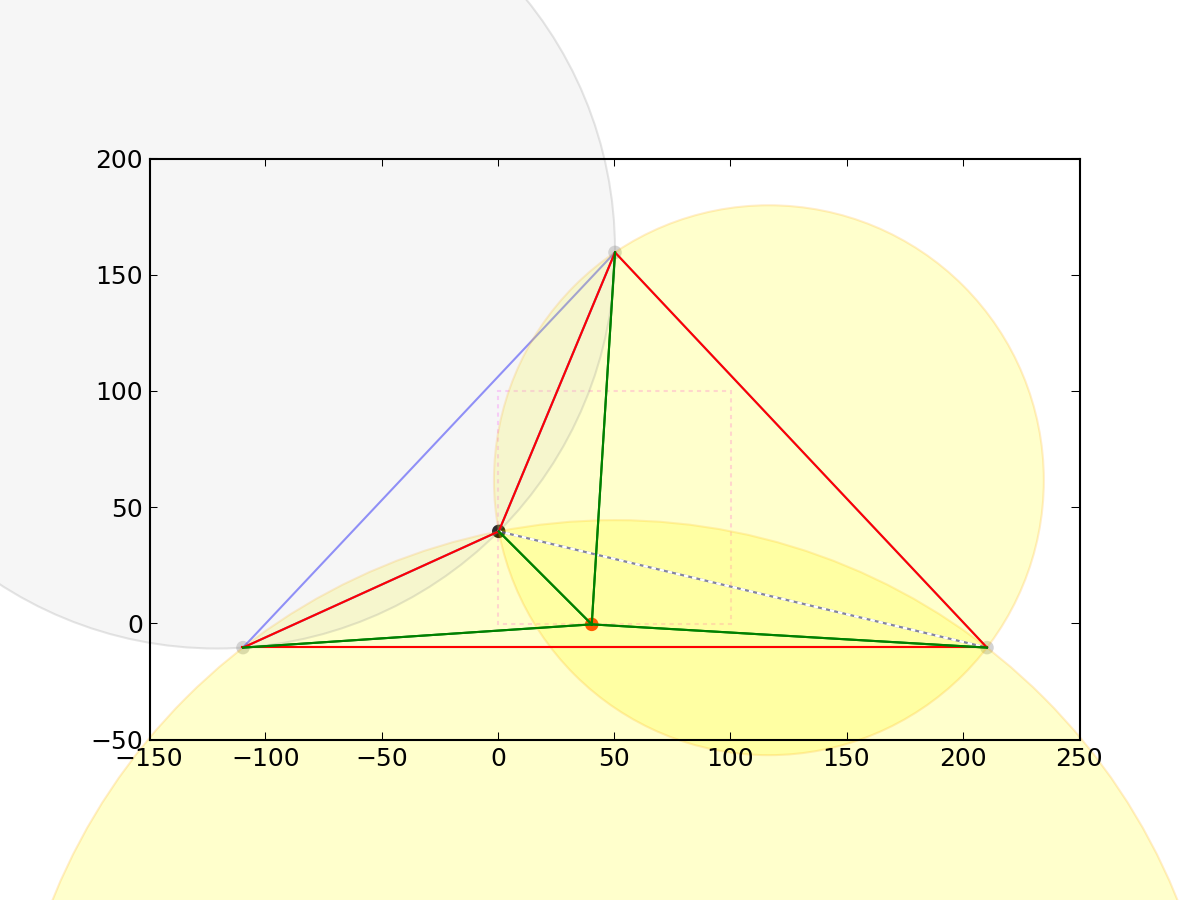
Insert third node

 

 

 

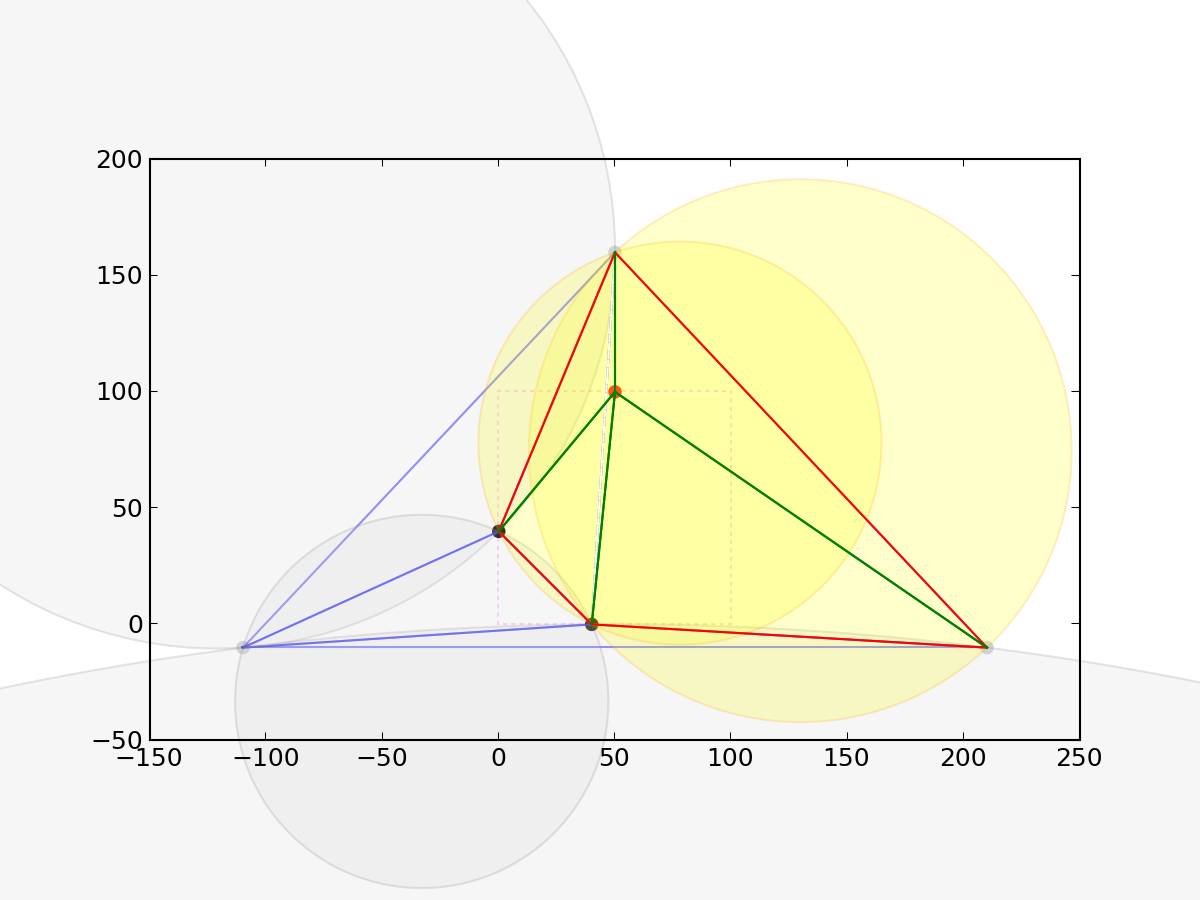
Insert fourth node

 

 

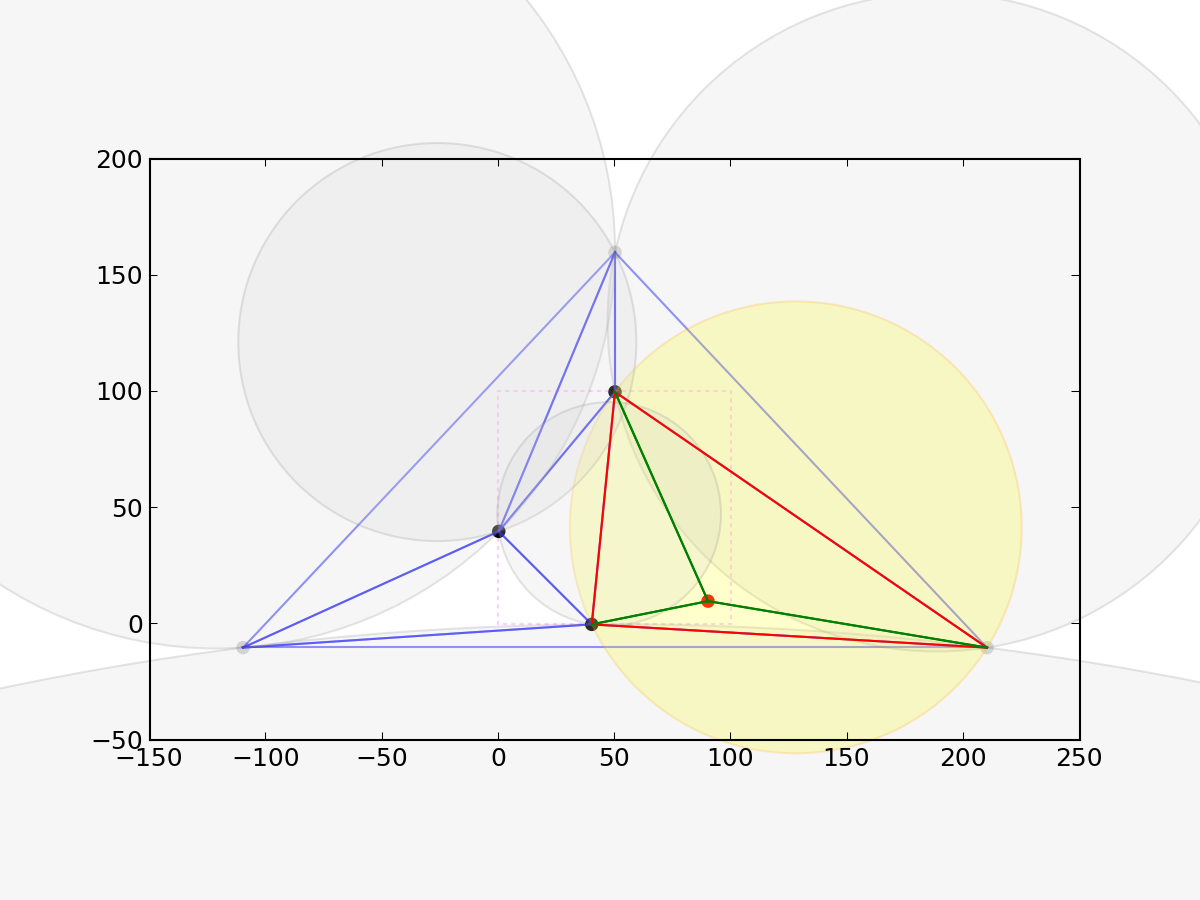
Insert fifth (and last) node

 

 

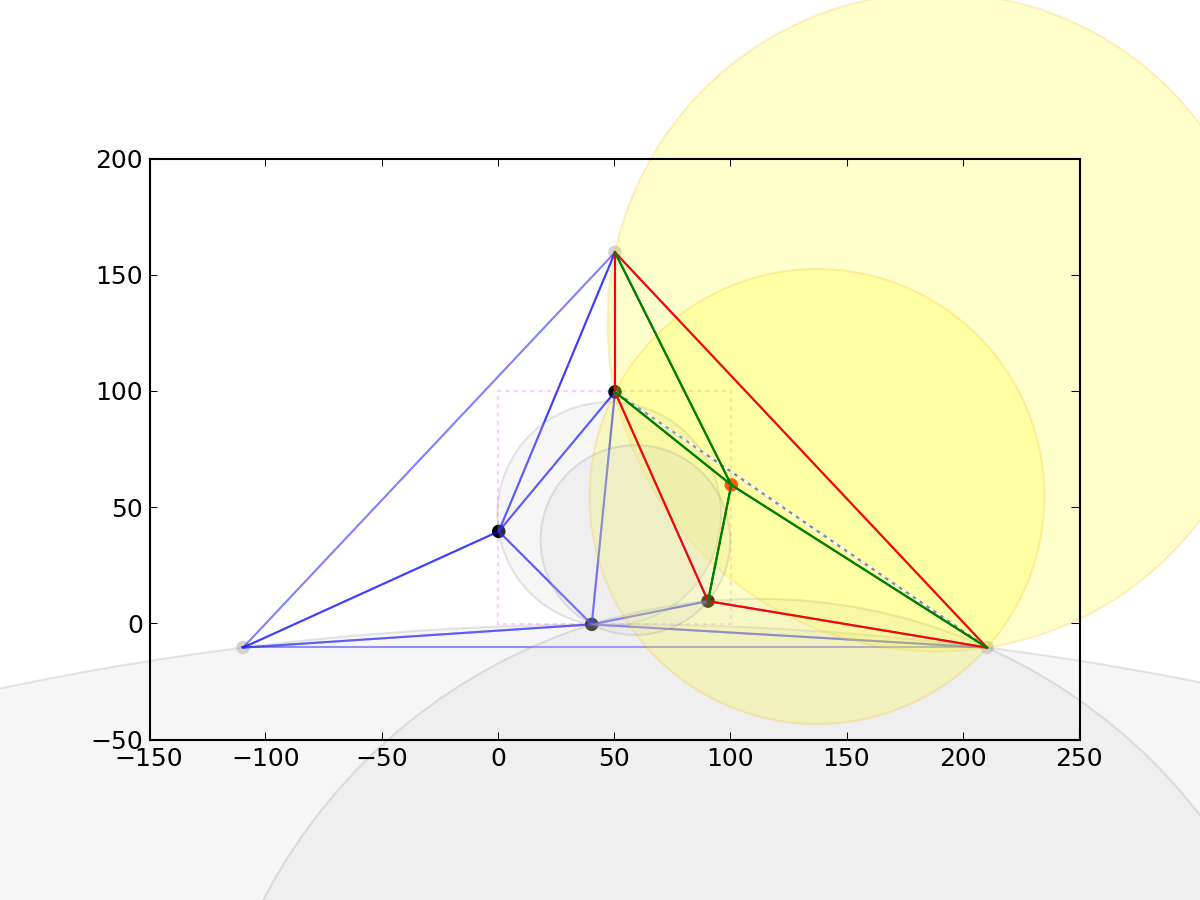
Remove edges with extremes in the super-triangle

 

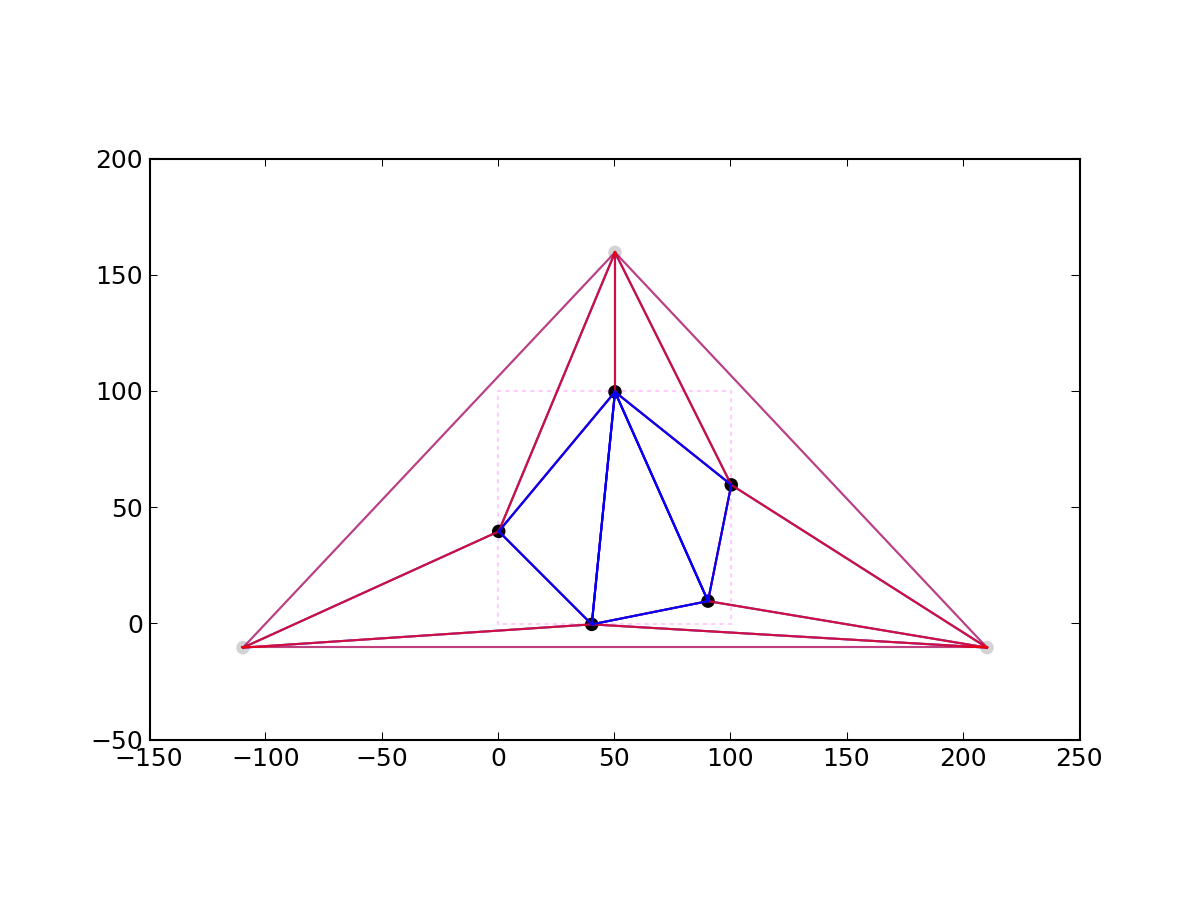
步骤

逐点插入算法中的Bowyer-Watson算法的基本步骤是：

1. 构造一个超级三角形，包含所有散点，放入三角形链表。

2. 将点集中的散点依次插入，在三角形链表中找出其外接圆包含插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，从而完成一个点在Delaunay三角形链表中的插入。

3. 根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入Delaunay三角形链表。

4. 循环执行上述第2步，直到所有散点插入完毕。

​ 这一算法的关键的第2步图示如下：

 

 

 

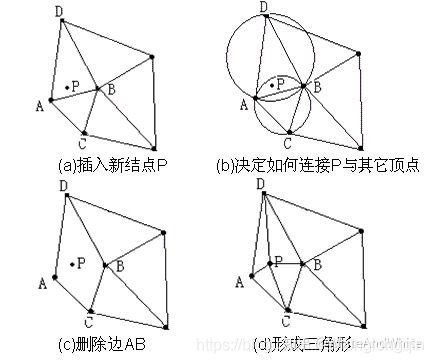
 BW算法伪代码

 

 1 function BowyerWatson (pointList)
 2     // pointList is a set of coordinates defining the points to be triangulated
 3     triangulation := empty triangle mesh data structure
 4     add super-triangle to triangulation // must be large enough to completely contain all the points in pointList
 5     for each point in pointList do // add all the points one at a time to the triangulation
 6         badTriangles := empty set
 7         for each triangle in triangulation do // first find all the triangles that are no longer valid due to the insertion 对应第2步：新插入点是否在三角形外接圆中
 8             if point is inside circumcircle of triangle
 9                 add triangle to badTriangles
10         polygon := empty set
11         for each triangle in badTriangles do // find the boundary of the polygonal hole 比如图中的ABCD
12             for each edge in triangle do
13                 if edge is not shared by any other triangles in badTriangles
14                     add edge to polygon
15         for each triangle in badTriangles do // remove them from the data structure
16             remove triangle from triangulation
17         for each edge in polygon do // re-triangulate the polygonal hole
18             newTri := form a triangle from edge to point
19             add newTri to triangulation

20     for each triangle in triangulation // done inserting points, now clean up 插完所有点了，现在清理掉外围的三角形，如下图中的蓝色三角形之外的三角形。
21         if triangle contains a vertex from original super-triangle
22             remove triangle from triangulation
23     return triangulation

 

 

参考链接：

https://en.wikipedia.org/wiki/Bowyer%E2%80%93Watson_algorithm

https://github.com/bl4ckb0ne/delaunay-triangulation

https://blog.csdn.net/longlongqin/article/details/104497533

posted @ 2023-05-21 10:45  blogzzt  阅读(475)  评论(0)  编辑  收藏  举报