理解回溯算法——从全排列问题开始
一、简介
回溯法（backtracking）是优先搜索的一种特殊情况，又称为试探法，常用于需要记录节点状
态的深度优先搜索。通常来说，排列、组合、选择类问题使用回溯法比较方便。
解题套路：
result = [] def backtrack(路径, 选择列表): if 满足结束条件: result.add(路径) return for 选择 in 选择列表: 做选择 backtrack(路径, 选择列表) 撤销选择
二、从全排列问题开始理解回溯算法
以数组 [1, 2, 3] 的全排列为例。
先写以 1开头的全排列，它们是：[1, 2, 3], [1, 3, 2]，即 1 + [2, 3] 的全排列（注意：递归结构体现在这里）；
再写以 2 开头的全排列，它们是：[2, 1, 3], [2, 3, 1]，即 2 + [1, 3] 的全排列；
最后写以 3 开头的全排列，它们是：[3, 1, 2], [3, 2, 1]，即 3 + [1, 2] 的全排列。
总结搜索的方法：按顺序枚举每一位可能出现的情况，已经选择的数字在 当前 要选择的数字中不能出现。按照这种策略搜索就能够做到 不重不漏。这样的思路，可以用一个树形结构表示。
看到这里的朋友，建议先尝试自己画出「全排列」问题的树形结构。
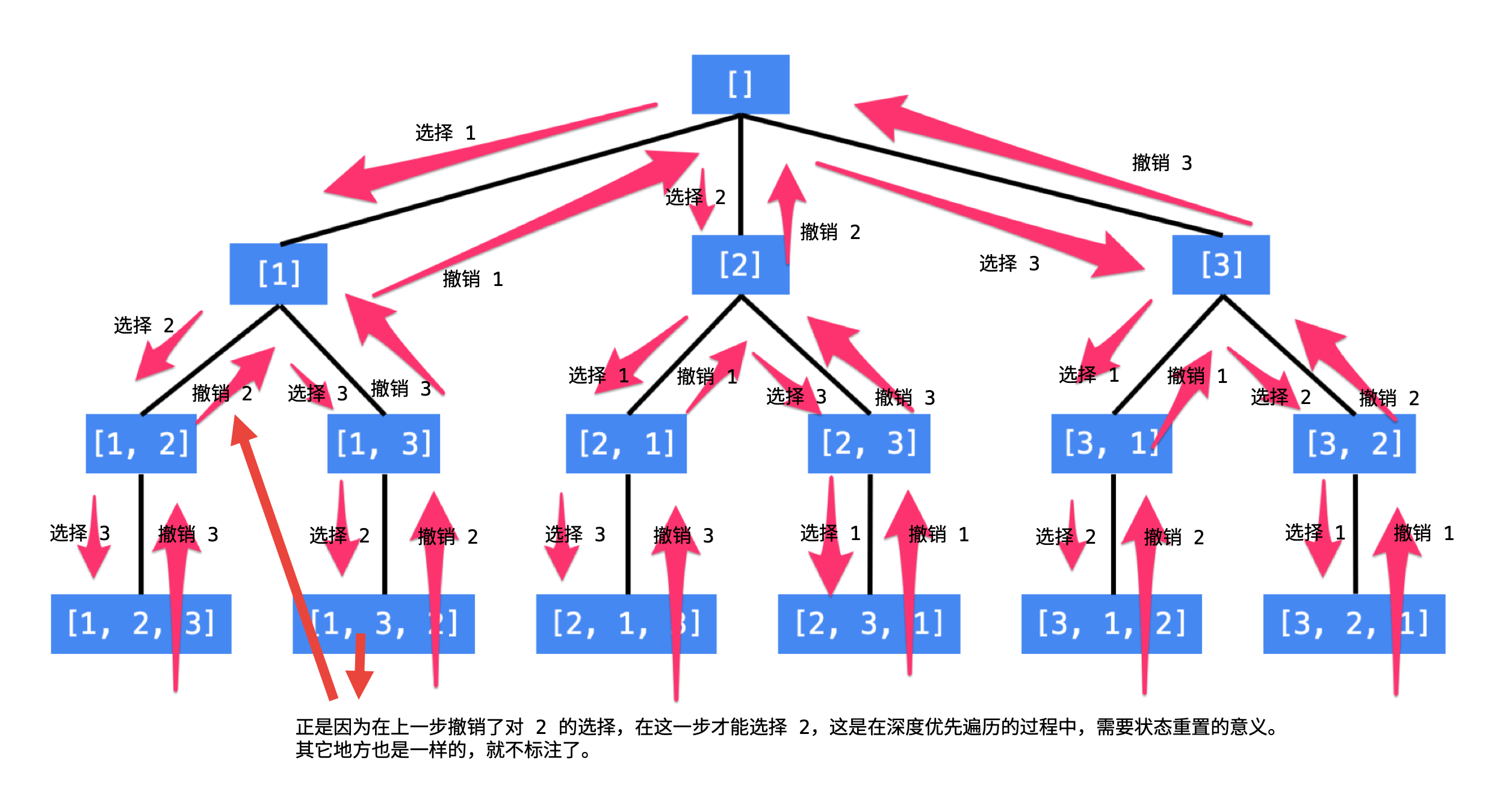
说明：
1、每一个结点表示了求解全排列问题的不同的阶段，这些阶段通过变量的「不同的值」体现，这些变量的不同的值，称之为「状态」；
2、使用深度优先遍历有「回头」的过程，在「回头」以后， 状态变量需要设置成为和先前一样 ，因此在回到上一层结点的过程中，需要撤销上一次的选择，这个操作称之为「状态重置」；
3、深度优先遍历，借助系统栈空间，保存所需要的状态变量，在编码中只需要注意遍历到相应的结点的时候状态变量的值是正确的，具体的做法是：往下走一层的时候，path 变量在尾部追加，而往回走的时候，需要撤销上一次的选择，也是在尾部操作，因此 path 变量是一个栈；
4、深度优先遍历通过「回溯」操作，实现了全局使用一份状态变量的效果。
使用编程的方法得到全排列，就是在这样的一个树形结构中完成 遍历，从树的根结点到叶子结点形成的路径就是其中一个全排列。
在具体的写法上，它与普通的深度优先搜索一样，都有[修改当前节点状态]->[递归子节点] 的步骤，只是多了回溯的步骤，变成了[修改当前节点状态]->[递归子节点]->[回改当前节点状态]。
三、题解
46. 全排列
1 class Solution: 2 def permute(self, nums: List[int]) -> List[List[int]]: 3 def dfs(nums, size, depth, path, used, res): 4 if depth == size: 5 res.append(path[:]) # 注意append方法是浅拷贝，如果用res.append(path)是不行的，最后输出的都是[] 6 return 7 8 # 在非叶子结点处，产生不同的分支，这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。 9 for i in range(size): 10 if not used[i]: 11 used[i] = True 12 path.append(nums[i]) 13 14 dfs(nums, size, depth + 1, path, used, res) 15 16 # 注意：下面这两行代码发生 「回溯」（需要做「状态重置」，即「回到过去」） 17 # 回溯发生在从 深层结点 回到 浅层结点 的过程，代码在形式上和递归之前是对称的 18 used[i] = False 19 path.pop() 20 21 size = len(nums) 22 if len(nums) == 0: 23 return [] 24 25 used = [False for _ in range(size)] 26 res = [] 27 dfs(nums, size, 0, [], used, res) 28 return res
注意：如果在每一个非叶子结点分支的尝试，都创建 新的变量 表示状态，那么不需要回溯算法。但是这样做会产生很多中间变量。
打印信息，看看回溯的具体过程
from typing import List class Solution: def permute(self, nums: List[int]) -> List[List[int]]: def dfs(nums, size, depth, path, used, res): if depth == size: res.append(path[:]) # 注意append方法是浅拷贝，如果用res.append(path)是不行的，最后输出的都是[] return # 在非叶子结点处，产生不同的分支，这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。 for i in range(size): if not used[i]: used[i] = True path.append(nums[i]) print(" 递归之前 => ", path) dfs(nums, size, depth + 1, path, used, res) # 递归 # 注意：下面这两行代码发生 「回溯」（需要做「状态重置」，即「回到过去」） # 回溯发生在从 深层结点 回到 浅层结点 的过程，代码在形式上和递归之前是对称的 used[i] = False path.pop() print("递归之后 => ", path, "used:", used) size = len(nums) if len(nums) == 0: return [] used = [False for _ in range(size)] res = [] dfs(nums, size, 0, [], used, res) return res if __name__ == '__main__': nums = [1, 2, 3] solution = Solution() res = solution.permute(nums) print(res)
打印结果如下：
递归之前 => [1] 递归之前 => [1, 2] 递归之前 => [1, 2, 3] 递归之后 => [1, 2] 递归之后 => [1] 递归之前 => [1, 3] 递归之前 => [1, 3, 2] 递归之后 => [1, 3] 递归之后 => [1] 递归之后 => [] 递归之前 => [2] 递归之前 => [2, 1] 递归之前 => [2, 1, 3] 递归之后 => [2, 1] 递归之后 => [2] 递归之前 => [2, 3] 递归之前 => [2, 3, 1] 递归之后 => [2, 3] 递归之后 => [2] 递归之后 => [] 递归之前 => [3] 递归之前 => [3, 1] 递归之前 => [3, 1, 2] 递归之后 => [3, 1] 递归之后 => [3] 递归之前 => [3, 2] 递归之前 => [3, 2, 1] 递归之后 => [3, 2] 递归之后 => [3] 递归之后 => [] [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
四、解法二：交换
这题使用回溯算法的还一种解决方式就是交换，比如我们先选择第一个数字，然后和后面的所有数字都交换一遍，这样全排列的第一位就确定了。然后第二个数字在和后面的所有数字交换一遍，这样全排列的第二位数字也确定了……，一直继续下去，直到最后一个数字不能交换为止，这里画个图来看一下
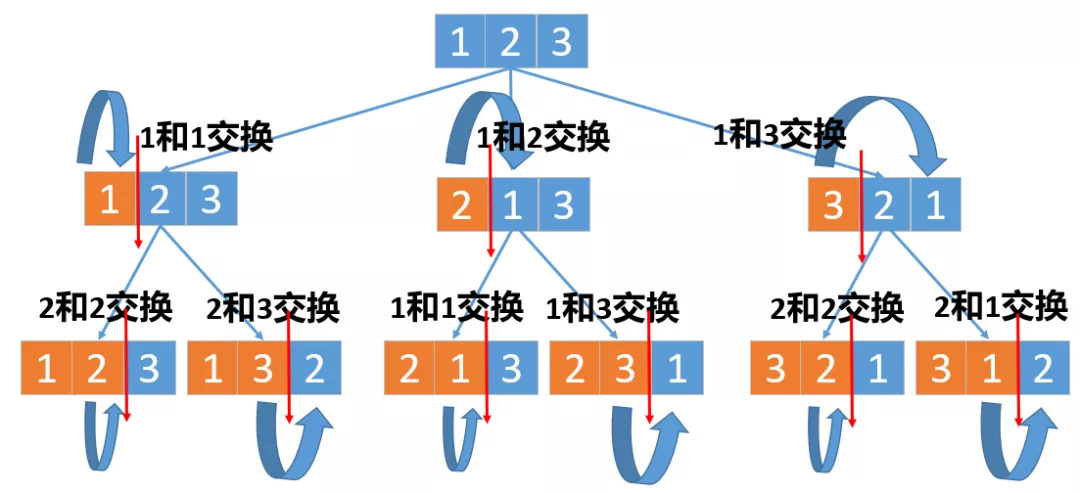
class Solution { public: vector<vector<int>> permute(vector<int>& nums) { vector<vector<int>> ans; backtrack(nums, 0, ans); return ans; } void backtrack(vector<int>& nums, int depth, vector<vector<int>>& ans) { if (depth == nums.size() - 1) { ans.push_back(nums); return; } for (int i = depth; i < nums.size(); ++i) { // 修改当前节点状态 swap(nums[i], nums[depth]); // 当前数字nums[i]要和后面所有的数字都要交换一遍（包括他自己） // 递归子节点 backtrack(nums, depth + 1, ans); // 回改当前节点状态 swap(nums[i], nums[depth]); } } };
参考链接：
https://leetcode.cn/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/
