动态规划解背包问题（01背包）
一、概念
问题可以描述为：给定一组物品（有N 个物品和容量为W 的背包，每个物品都有自己的体积w 和价值v），在限定的总重量内，我们如何选择，才能使得物品的总价格最高。
常见的有01背包问题，即限定每种问题只能取0个或1个。
问：要使背包装的物品价值最大，应该怎么选，最大值是多少？
二、动态规划解法
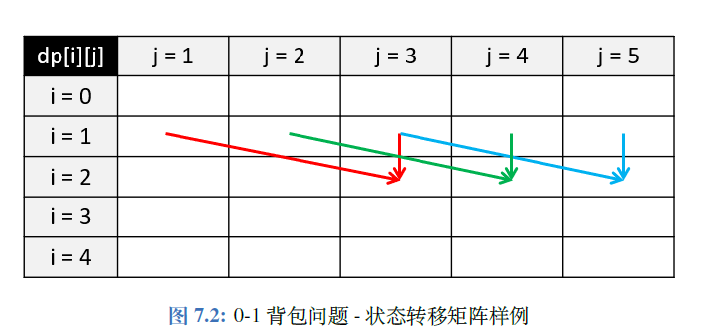
动态规划数组dp[i][j]含义：前i件物品，放入容量为j的背包里的最大价值。
递推公式：dp[i][j] = max(不放物品i所能达到的最大价值，放物品i所能达到的最大价值)
其中，
不放物品i所能达到的最大价值：dp[i-1][j]
放物品i所能达到的最大价值：dp[i-1][j - weight[i]] + value[i]，需判断 j > weight[i]
| dp[i][j] | j = 0 | 1 | 2 | 3 | 4 |
| i = 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 15 | 15 | 15 | 15 |
| i = 2 | 0 | 15（不放第i件） | 0+20=20 | 15+20=35 | 15+20=35 |
| i = 3 | 0 | 15（不放第i件） | 20 （不放第i件） | 35 （不放第i件） | 35 （不放第i件） |
背包问题不需要排序，即使改变物品顺序，也不影响。
代码如下：N表示物品数量，W表示背包容量
三、空间优化
