二分图与染色算法

二分图的概念

二分图就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。

 

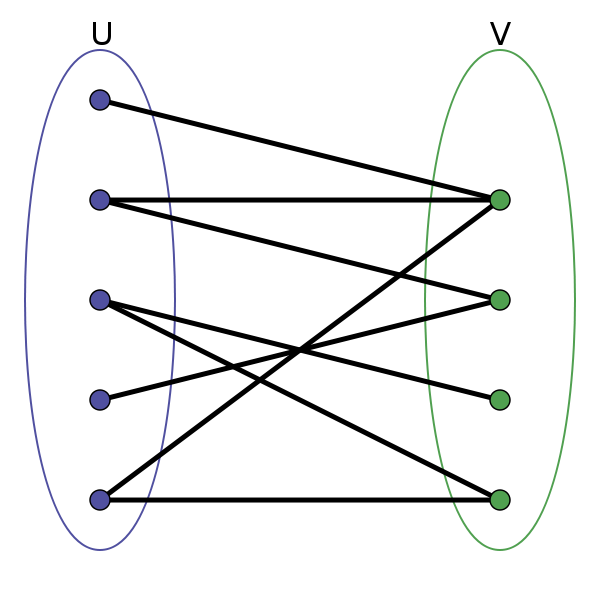
染色法概念

 

 

 

二分图算法也称为染色法。如果可以用两种颜色对图中的节点进行着色，并且保证相邻的节点（边两端的节点）颜色不同，那么图为二分。

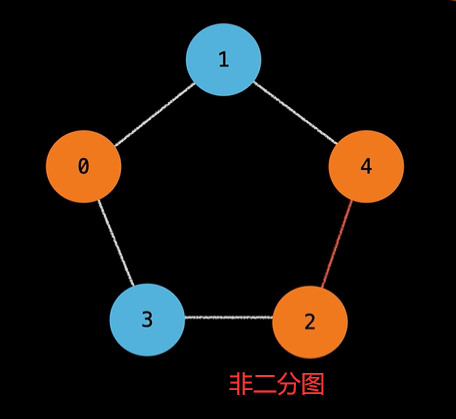
下图中有相邻节点的颜色相同，因此不是二分图。

 

 

 

 

题目与解析

lc 785. 判断二分图

 

 

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        vector<int> color(graph.size(), -1);  // 各节点的着色情况，-1:未着色 0:颜色A，1:颜色B；
        stack<int> colorStack;  // 用于完成深度优先遍历的栈
        // 对图中的每个节点进行DFS，因为可能存在孤立点
        for (int i = 0; i < graph.size(); i++) {
            if (color[i] == -1) {
                colorStack.push(i);  
                color[i] = 0;
                // 对该点进行DFS
                while (!colorStack.empty()) {
                    // 将栈顶点出栈
                    int index = colorStack.top();
                    colorStack.pop();
                    // 对所有栈顶点的相邻节点判断
                    for (int j = 0; j < graph[index].size(); j++) {
                        if (color[graph[index][j]] == -1) {  // 若未着色
                            color[graph[index][j]] = color[index] ^ 1;
                            colorStack.push(graph[index][j]);  // 将着色正确的节点入栈
                        }
                        else { // 若着色
                            if (color[graph[index][j]] ^ color[index] == 0) {  // 若颜色相同
                                return false;
                            }
                        }
                    }
                }
            }
        }
        return true;
    }
};