算法打基础——HashⅡ: 全域哈希与完美哈希
这一节涉及数学超级多，各种数论知识，各种不明觉厉！ 看了几遍，才勉强看懂一些，所以这
篇稍微简单的介绍着两种hash table, 免得瞎说说错了。
这一讲的主要知识点是：1. 全域哈希及构造 2. 完美哈希
1. 全域哈希及构造
介绍全域哈希之前，要先讨论一下普通哈希的一个缺点。 举个charles举得那个例子：如果你
和一个竞争对手同时为一家公司做compiler的symbol table, 公司要求你们代码共享
(o(╯□╰)o)，你们做好后公司评判的标准就是 你俩互相提供一些测试样例，谁的效率高就买谁的。
然后，普通哈希的缺点就出来了：对任意的hash函数h,总存在一组keys，使得
, 对某个槽i。即我总可以找到一组键值，让他们都映射到同一个槽里面，这样效率
就跟离链表差不多了
解决的思想就是：独立于键值，随机的选择hash 函数。这就跟快排中为避免最差情况时随机化
版本差不多。但是选取hash function的全局域是不能乱定的，否则也打不到理想的性能。
下面就给出全域哈希的定义：
设U是key的全局域， 设\(\mathcal{H}\) 是哈希函数的有限集合，每一个都是将U映射到
{0,1,..,m-1},即table的槽内。 如果对所有不等的\(x,y\in U\),有
换句话说，就是对于任意的不相等key的x和y, 从哈希函数集中选择一个哈希函数，这两个key
发生冲突的概率是1/m
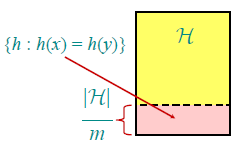
更形象的，当我随机选一个哈希函数时，就像在上图区域乱扔一个飞镖，落在下面红色区域中
就会发生冲突，这个概率是1/m
下面给一个定理，说明为什么全域函数就是好的：
设h是从哈希函数全域集\(\mathcal{H}\)中随机选出的函数h. h被用作把任意n个键映射到表T的m个
槽中，对给定键值x,我们有：
定理：E[#collision with x]<n/m
Proof: 设\(C_x\)是表示与key x冲突的键值数量的随机变量，设\(c_{xy}\)是指示变量，即
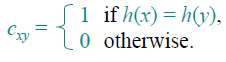
则，\(E[c_{xy}]=1/m\) 且\(C_x=\sum_{y\in T-\{x\}}c_{xy}\)，则
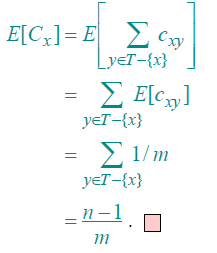
证毕！
这个定理想要说明的是，这种全域哈希的随机化选择可以达到哈希表理想的效果。注意这里
n/m是之前定义过的load factor
现在给出一种构造全域哈希的方法：
首先选择一个足够大的质数p,使得所有的键值都在0-p-1之间。且设\(Z_p\)表示{0,1,...,p-1},设
\(Z_p^*\)表示{1,2,..,p-1}. 因为槽m的数量少于key的数量，所有m<p.
然后我们就可以设计哈希函数了，设任意的\(a\in Z_P^*,b\in Z_p\),然后
\(h_a,b(k)=((ak+b)mod p)mod m\)
所有这样的哈希函数族为:
\(\mathcal{H}_{p.m}=\{h_{a,b}:a\in Z_p^*, b\in Z_p\}\)
例如：选定p=17，m=6,\(h_{3,4}(8)=5\). 每个哈希函数都是将\(Z_p\)映射到\(Z_m\). 我们还
可以看到这个哈希函数族共有p(p-1)个哈希函数
针对这种构造方法构造出的是全域哈希函数的证明就略过了，涉及数学知识确实比较多，讲不好。
2. 完美哈希
当键值是static(即固定不变)的时候，我们可以涉及方案使得最差情况下的查询性能也很出色，这就是
完美哈希。实际上，很多地方都会用到静态关键字集合。比如一种语言的保留字集合，一张CD-ROM
里的文件名集合。 而完美哈希可以在最坏情况下以O(1)复杂度查找，性能非常出色的。
完美哈希的思想就是采用两级的框架，每一级上都用全域哈希
完美哈希的结构如上图。具体来说，第一级和带链表的哈希非常的相似，只是第一级发生冲突后后面接
的不是链表，而是一个新的哈希表。后面那个哈希结构，我们可以看到前端存储了一些哈希表的基本
性质：m 哈希表槽数；a,b 全域哈希函数要确定的两个值(一般是随机选然后确定下来的)，后面跟着
哈希表。
为了保证不冲突，每个二级哈希表的数量是第一级映射到这个槽中元素个数的平方，这样可以保证整个
哈希表非常的稀疏。下面给出一个定理，能更清楚的看到设置m=n^2的作用
定理：设\(\mathcal{H}\)是一类全域哈希函数，哈希表的槽数m=n^2. 那么，如果我们用一个随机
函数\(h\in\mathcal{H}\)把n个keys映射到表中。冲突次数的期望最多是1/2.
Proof:根据全域哈希的定义，对任意选出的哈希函数h，表中2个给定keys冲突的概率是1/m,即1/n^2
且总共有\(C_n^2\)可能的键值对，那么冲突次数的期望就是
\(C_n^2\cdot 1/n^2=n(n-1)/2\cdot 1\n^2 < 1/2\) 证毕！
为了冲突的理解从期望转换到概率，引入下面这个推论
推论： 完美哈希没有冲突的概率至少是1/2
Proof: 这里主要要用到一个不等式Markov's inequality-对任意非负随机变量X，我们有
Pr{X≥t}≤E[x]/t
利用这个不等式，让t=1,即可得到冲突次数大于1的概率最多为1/2
因为第二层每个表槽的个数是这个表中元素n^2，可能会感觉到这样存储空间会很大，实际上，可以证
明\(E[\sum_{i=0}^{m-1}\Theta(n_i^2)]=\Theta(n)\), 因为证起来蛮复杂，所以我也略过了%>_<%
最后，向各位大牛们提个问题，看到了请一定要教我！ 怎么在博客园里面更美观的插入大量数学公式
(最好是用latex语法)，支持分多行对齐等结构，现在不会，证明公式都没办法写，写出来也难看。跪谢！
