算法打基础——算法基本分析

因为基础实在太差，决定从看算法导论视频+书开始重新打打基础，希望能坚持下来！！

第一节 算法基本分析

个人认为 本节的主要知识点有：

1 插入排序及其分析     2 算法复杂度基本符号  3 merge sort及其分析

 

1 插入排序及其分析

插入排序伪代码：

INSERTION-SORT (A, n) ⊳A[1 . . n]

    for j ←2 to n

        do key ←A[ j]

             i ←j –1

             while i > 0 and A[i] > key

                    doA[i+1] ←A[i]

                        i ←i –1

                A[i+1] = key

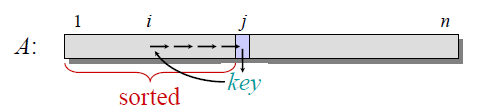
排序算法的关键就是那个key，过程是，从第二个开始往后，将key元素插到前面的元素中去（注意：前面的元素永远都是排序过的元素），

找到比这个key小的停下来就ok了

 

2 算法复杂度基本符号

我们先介绍复杂度基本符号，然后再分析插入排序。 算法基本符号： big O ;big omega; big theta 

f = O(g) 是说存在一个N,当n>N的时候有 f(n) < c * g(n),说明增长趋势不会超过g(n)的趋势              上界！
f = Ω(g) 是说存在一个N,当n>N的时候有 f(n) > c * g(n),说明增长趋势至少会有g(n)的趋势              下界！
f = Θ(g) 是说存在一个N,当n>N的时候有 c1 * g(n) < f(n) < c2 * g(n),说明增长趋势和g(n)一样       准确界！

 

然后我们来分析插入排序的复杂度：

插入排序的最差情况是当序列是逆序的时候，每个元素都要和前面所有的元素交换位置，

复杂度： 

平均情况是当前序列期望的交换次数是前面元素的一半的时候，

复杂度： 

 

 

3. merge sort 及其相关分析

 merge sort的主要思想是分治法，将一个序列分到只有一个元素，然后再按一定规则合并，自然就排序了。其主要过程就是两个：分！ 合！

伪代码如下：

MERGE-SORT A[1 . . n]

1.      If n= 1, done.

2.      Recursively sort A[ 1 . . low(n/2)]

          and A[ up(n/2)+1 . . n ] .

3.     “Merge” the 2 sorted lists.

然后是非常重要的merge过程：

merge 过程的伪代码非常的复杂，但是其叙述过程很简单，就是两个（已！排！序！）的序列，合并时去每个的头部，谁小就将其插

到结果序列中，删去改头部，重复这个过程，知道所有元素处理完毕！（merge sort实现还是蛮难的，值得一试）

merge sort 有趣的一点就是其复杂度分析（涉及到递归树）

2T(n/2)严格来说 应该是 T(up(n/2))+T(down(n/2))

则 归并排序的复杂度为

这个复杂度是用递推公式来表达的，当然可以用数学方法来求，但是这里我们可以用递归树来求！

Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.

归并排序的复杂度是nlogn 而插入排序的复杂度是n^2, 但是插入排序处理小规模数据的时候速度还是很快的。据说当数据<30时

插入快于归并（原因？应该可以推的）

最后附上写的插入 和 归并排序的代码：

/////////////////////////CLRS   video lec1  选择排序///////////////////////////////////////////////////
//
//  已插入排序为主，还涉及到产生随机某个范围的数(时间种子)；

#include<iostream>
#include<cstdlib>
#include<ctime>
#define random(x)(rand()%x)

using namespace std;

int main()
{
    int a[100];
    clock_t start,finish;
    double funtime;
    srand((int)time(0));
    for(int i=0;i<100;i++)
        a[i] = random(200);    
    int key,j;
    start = clock();
    for(int i=1;i<100;i++)
    {
        key = a[i];
        j=i-1;
        while(j>=0&&a[j]>key)
        {
            a[j+1] = a[j];
            j--;
        }
        a[j+1] = key;
    }
    finish = clock();
    for(int i=0;i<100;i++)
    {
        cout<<a[i]<<" ";
    }
    cout<<endl;
    funtime=(double)(finish-start);
    cout<<funtime<<endl;
    return 0;
}

    

/////////////////////////CLRS   video lec1  归并排序///////////////////////////////////////////////////
//


#include<iostream>
#include<cstdlib>
#include<ctime>
using namespace std;

#define random(x)(rand()%x)
#define INF 0x3f3f3f3f

void merge(int* arr, int begin, int end)
{
    int middle;
    middle = (end+begin)/2;
    int numl = middle - begin +1;
    int numr =end -( middle+1)  +1;
    int* arrl = new int[numl+1];
    int* arrr = new int[numr+1];
    for(int i=0;i<numl;i++)
    {
        arrl[i] = arr[begin+i];
    }
    arrl[numl] = INF;
    for(int i=0;i<numr;i++)
    {
        arrr[i] = arr[middle+1+i];
    }
    arrr[numr] = INF;
    int recl = 0; int recr = 0;
    for(int i=0;i<(end-begin+1);i++)
    {
        if(arrl[recl]<arrr[recr])
        {
            arr[begin+i] = arrl[recl++];
        }
        else{
            arr[begin+i] = arrr[recr++];
        }
    }
}




void merge_sort(int* arr, int begin, int end)
{
    int middle;
    if(begin<end)
    {
        middle = (end + begin)/2;           // 计算分割后的下标！
        merge_sort(arr,begin,middle);
        merge_sort(arr,middle+1,end);
        merge(arr,begin,end);
    }
}


int main()
{
    srand(time(0));
    int i,j,k;
    int a[100];
    cout<<"origin array: ";
    for(i=0;i<100;i++)
    {
        a[i]=random(500);        
        cout<<a[i]<<" ";
    }
    cout<<endl;

    merge_sort(a,0,100-1);
    for(i=0;i<100;i++)
        cout<<a[i]<<" ";
    return 0;

}