图
1.学习总结(2分)
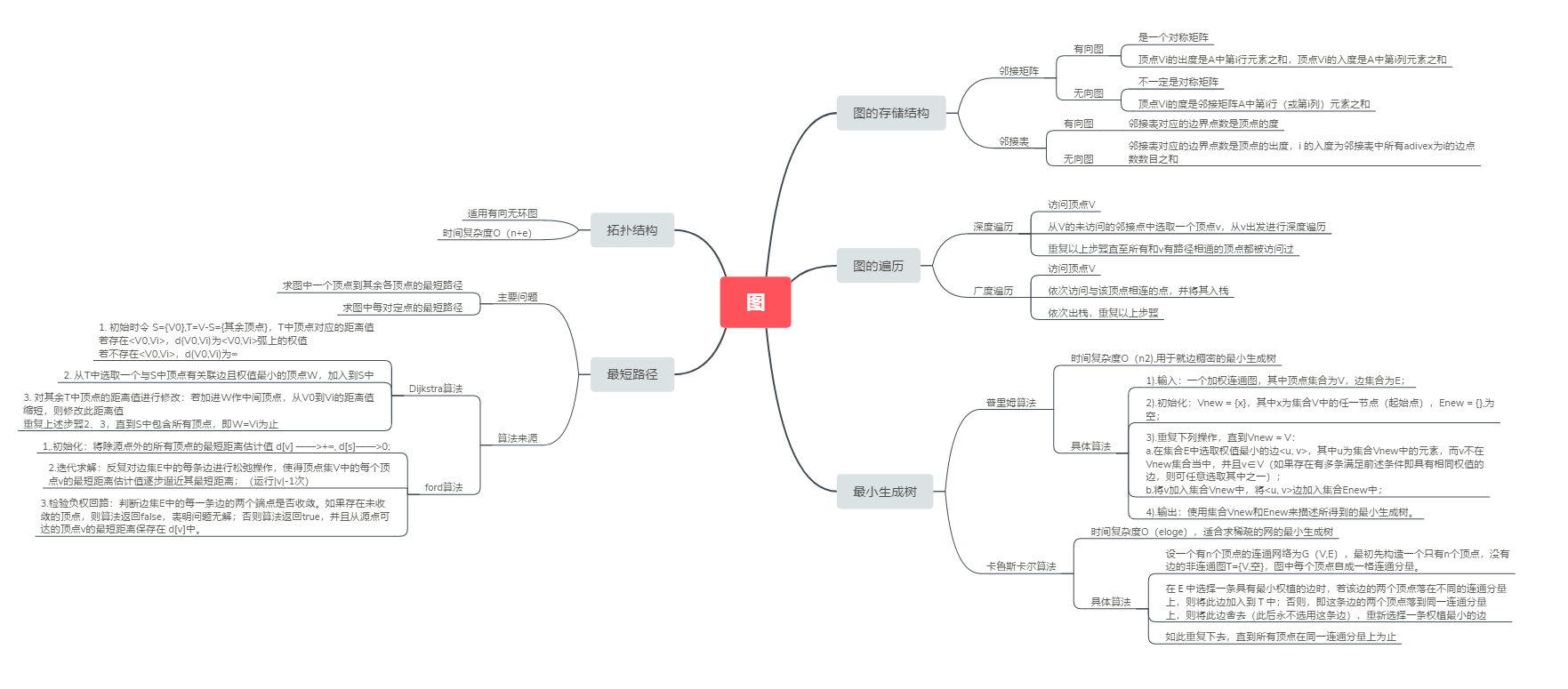
1.1图的思维导图
1.2 图结构学习体会
深度遍历广度遍历
- 深度优先遍历:从初始访问结点出发,我们知道初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点。总结起来可以这样说:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
- 广度遍历:从图中某个顶点V0出发,并访问此顶点;从V0出发,访问V0的各个未曾访问的邻接点W1,W2,…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点;
Prim和Kruscal算法
- 克鲁斯卡尔算法:基本思想是以边为主导地位,始终选择当前可用(所选的边不能构成回路)的最小权植边。所以Kruskal算法的第一步是给所有的边按照从小到大的顺序排序。这一步可以直接使用库函数qsort或者sort。接下来从小到大依次考察每一条边(u,v)。
- Prim算法:求最小生成树的时候和边数无关,和顶点树有关,所以适合求解稠密网的最小生成树。
Dijkstra算法
- 在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短值。
拓扑排序算法 - 对一个有向无环图G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。
2.PTA实验作业(4分)
题目1:7-1 图着色问题
2.2 设计思路
建图
然后调用深度遍历函数将深度遍历结果储存于数组d中
输入颜色分配方案数目n
while(n--)
{
for i=1 to 顶点数
输入颜色方案并计算颜色数目
判断颜色数目是否与k相等,不等令flag=0
将颜色按深度遍历排序储存在数组e中
for i=0 to 顶点数
for j=0 to 顶点数
如果g->a[d[i]][d[j]]==1即存在边且e[i]==e[j]颜色相等
令flag=0且退出循环
如果flag=0 输出no 否则 输出yes
}
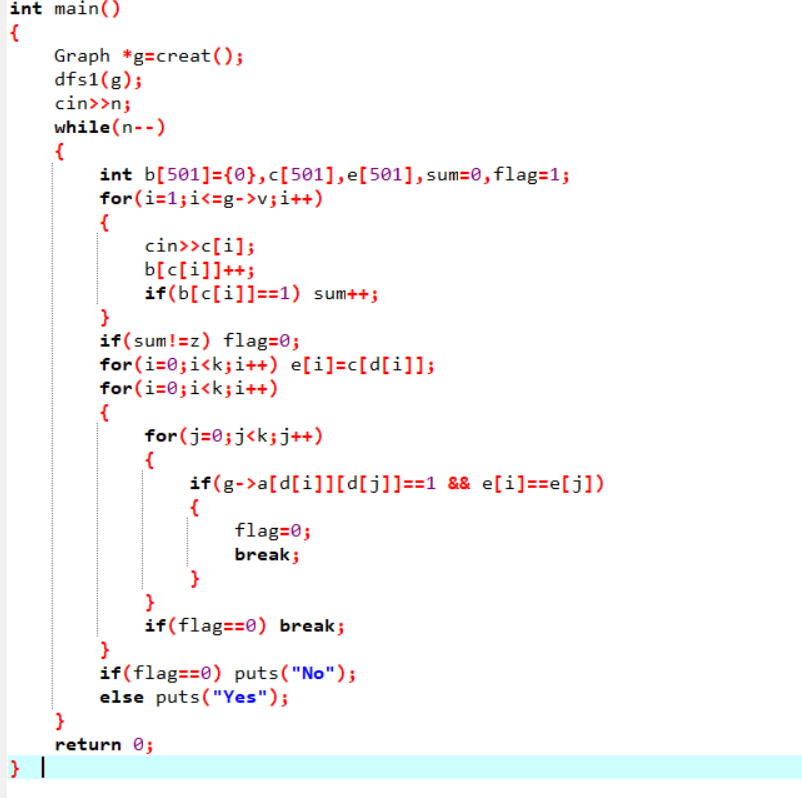
2.3 代码截图
2.4 PTA提交列表说明。

题目2:7-2 排座位
2.2 设计思路
主函数{
输入宾客总人数N,两两宾客之间的关系数M , 查询的条数K
调用建图函数Create()
调用关系函数 Relation()
}
建图函数Create() {
先初始化图g
for i=1 to e{
输出两个顶点编号k,l和两者关系m
让(k,l)和(l,k)赋值m
}
}
关系函数 Relation(){
for l=1 to k{
输入两个顶点i,j
如果两个关系为1 输出 No problem
否则如果两个关系为0 输出 OK
否则{
先检查他们是否有共同朋友若有flag=1
判断flag是否为1{
如果flag为1 输出 OK but... flag=0
否则 输出 No way
}
}
}
}
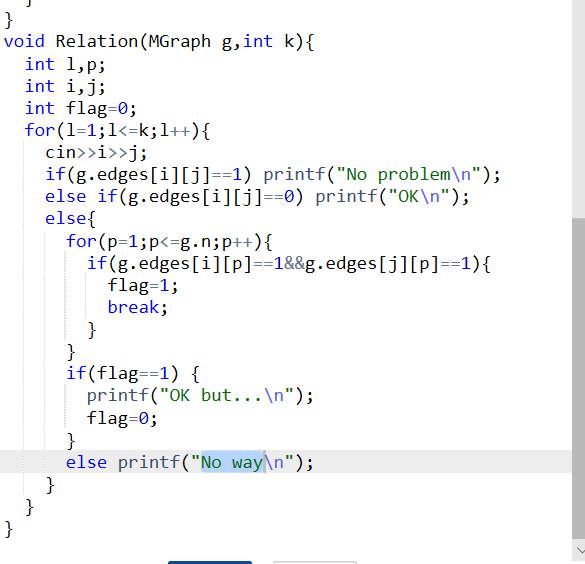
2.3 代码截图
2.4 PTA提交列表说明。
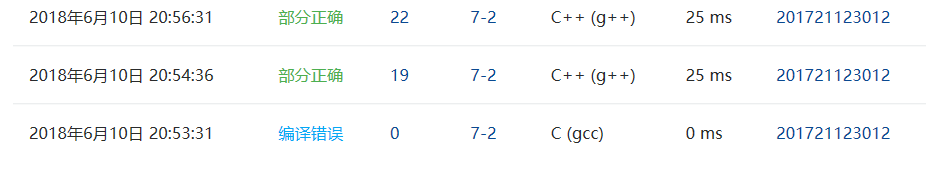
第一次错误是最大N的段错误,我看了发现MAXV只有100,会照成空间不够,改成101即正确
题目3:7-3 六度空间
2.2 设计思路
主函数{
输入顶点数n边数e建图
for i=1 to n {
count=1
广度遍历编号为i的顶点
}
}
广度遍历BFS{
hile(队列不为空)
{
第一个元素出队 并存入de
for i=0 to n-1
如果G[de][i] && !visited[i]
visited[i] = true代表已判断过
将i进队
count加一
tail=i
如果de=last
层数加一
last=tail
如果层数等于6 退出循环
}
返回count
}
2.3 代码截图
2.4 PTA提交列表说明

- 本题无问题
3.截图本周题目集的PTA最后排名(3分)

3.1 PTA排名(截图带自己名字的排名)
- 100
3.2 我的总分:
- 137
4. 阅读代码(必做,1分)
#define MAXV 10001
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include<queue>
using namespace std;
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
int visited[MAXV];
int flag=0;
void CreateAdj(AdjGraph *&G,int n,int e); //创建图邻接表
void BFS(AdjGraph *G,int v); //v节点开始广度遍历
int main()
{
AdjGraph *G;
int n,e,i,v;
cin>>n>>e;
CreateAdj(G,n,e);
for(int j=1;j<=G->n;j++){
for(i=1;i<=G->n;i++) visited[i]=0;
BFS(G,j);
}
return 0;
}
/* 请在这里填写答案 */
void CreateAdj(AdjGraph *&G,int n,int e)//创建图邻接表
{
ArcNode *p;
G=new AdjGraph;
for(int i=0;i<=n;i++){
G->adjlist[i].firstarc=NULL;
}
for(int i=0;i<e;i++){
int a,b;
cin>>a>>b;
p=new ArcNode;
p->adjvex=b;
p->nextarc=G->adjlist[a].firstarc;
G->adjlist[a].firstarc=p;
p=new ArcNode;
p->adjvex=a;
p->nextarc=G->adjlist[b].firstarc;
G->adjlist[b].firstarc=p;
}
G->n=n;
G->e=e;
}
void BFS(AdjGraph *G,int a) //v节点开始广度遍历
{
int w,u=0,last,size=0;
ArcNode *p;
queue<int>number;
visited[a]=1;
number.push(a);
u++;
last=a;
while(!number.empty()&&u<=6){
w=number.front();
number.pop();
p=G->adjlist[w].firstarc;
while(p!=NULL){
if(visited[p->adjvex]==0)
{
visited[p->adjvex]=1;
number.push(p->adjvex);
}
p=p->nextarc;
}
if(last==w){
last=number.back();
u++;
}
}
for(int i=1;i<=G->n;i++)
if(visited[i]==1)size++;
printf("%d: %.2f%%\n",a,1.0*size/G->n*100);
}
这个代码是我找舍友拿的自己做的时候没有去考虑这个空间复杂度的问题因此出错,而他的代码比较比较清楚的解决了这个问题,
最值得学习的应该是他这个记录每一层次的思想和last和层次的设计,这种类似层次遍历的算法值得学习。





