图的遍历- 广度优先遍历
广度优先遍历 breadth first search BFS
图的深度优先遍历类似与树的前序遍历, 广度优先遍历类似与树的 层序 遍历。
void printNodeByLevel(NODE* root)//Tree层序遍历
{
if(root == NULL)
{
return;
}
vector<NODE*>vec;
vec.push_back(root);
int cur=0;
while(cur<vec.size())
{
cout<<vec[cur]->data<<" ";
if(vec.[cur]->left != NULL)
{
vec.push_back(vec.[cur]->left);
}
if(vec.[cur]->right != NULL)
{
vec.push_back(vec.[cur]->right);
}
++cur;
}
cout<<endl;
}类似于一个分层搜索的过程,广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来访问这些结点的邻接结点。
具体算法表述如下:
-
访问初始结点v并标记结点v为已访问。
-
结点v入队列
-
当队列非空时,继续执行,否则算法结束。
-
出队列,取得队头结点u。
-
查找结点u的第一个邻接结点w。
-
若结点u的邻接结点w不存在,则转到步骤3;否则循环执行以下三个步骤:
1). 若结点w尚未被访问,则访问结点w并标记为已访问。 2). 结点w入队列 3). 查找结点u的继w邻接结点后的下一个邻接结点w,转到步骤6。
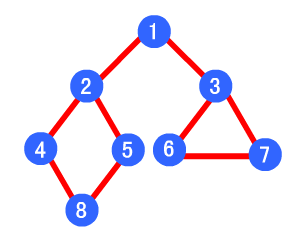
如下图,其广度优先算法的遍历顺序为:1->2->3->4->5->6->7->8
广度遍历-邻接矩阵
bool visited[MAX];
void BFSTraverse(MGraph G)
{
for(int i=0;i<G.numV; i++)
{
visited[i] = false;
}
Queue tempQ;
InitQueue(& tempQ);//初始化建立一个队列
for(int i=0;i<G.numV; i++)
{
if(! visited[i])//如果没访问过就处理
{
visited[i] = true;
cout<<G.ArrVex[i];
enQueue(&Q,i)//将此顶点入队列
while(! QueueEmpty(Q))//如果当前队列不为空
{
DeQueue(&Q,&i);//将队中元素出队列 赋值给i;
for(int j=0;j<G.numV;j++)
{
if(G.arc[i][j]==1 && !visited[j])
{
visited[j] = true;
cout<< G.ArrVex[j];
EnQueue(&Q,j);
}
}
}
}
}
}邻接表
邻接表 BFS 遍历
bool visited[MAX];
void BFSTraverse(MGraph G)
{
for(int i=0;i<G.numV; i++)
{
visited[i] = false;
}
Queue tempQ;
InitQueue(& tempQ);//初始化建立一个队列
for(int i=0;i<G.numV; i++)
{
if(! visited[i])//如果没访问过就处理
{
visited[i] = true;
cout<<G.adjlist[i].data;
enQueue(&Q,i)//将此顶点入队列
while(! QueueEmpty(Q))//如果当前队列不为空
{
DeQueue(&Q,&i);//将队中元素出队列 赋值给i;
EdgeNode* p =NULL;
p=G.adjlist[i].firstedge;
while(p)
{
if(!visited[p->adjvex])
{
visited[p->adjvex] = true;
cout<< adjlist[j].data;
EnQueue(&Q,j);
}
p=p->next;
}
}
}
}
}
关注公众号 海量干货等你