欧拉角
欧拉角是在空间中 描述从一个用于表示某个固定的参考系的、已知的方向,经过一系列基本旋转得到、新的代表另一个参考系的方向的方式。
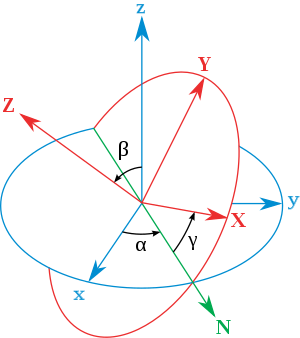
这个方向可以被想成从一个初始的方向,旋转到其确切位置的方向。如下图中描述,原始的参考系的坐标轴被定义为x,y,z,旋转后的坐标系
的坐标轴被定义为X,Y,.在几何和物理中,被旋转的坐标系通常被想象成严格附着在一个刚体上。因此,它被称为一个“本地”坐标系,这也意味着
它既代表这个刚体的位置,也代表这个刚体的方向。
欧拉角的几何定义是基于上面提及的(原始的和经过旋转的)的参考系的坐标轴和一个附加的、被称作 交轨线 的轴做出的。
交轨线(N)是xy和XY坐标平面相交处的一条线。换句话说,这条线,穿过这两个坐标系原点,并且垂直于zZ平面,这三个
欧拉角被如下定义:
- α (or
![\varphi]() ) x轴和N轴之间的角度。
) x轴和N轴之间的角度。 - β (or
![\theta]() ) z轴和Z轴之间的角度。
) z轴和Z轴之间的角度。 - γ (or
![\psi]() ) N轴和X轴之间的角度。
) N轴和X轴之间的角度。
你以为你在合群,其实你在浪费青春



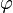
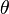 ) z轴和Z轴之间的角度。
) z轴和Z轴之间的角度。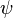

 浙公网安备 33010602011771号
浙公网安备 33010602011771号