Java - PriorityQueue

JDK 10.0.2

前段时间在网上刷题，碰到一个求中位数的题，看到有网友使用PriorityQueue来实现，感觉其解题思想挺不错的。加上我之前也没使用过PriorityQueue，所以我也试着去读该类源码，并用同样的思想解决了那个题目。现在来对该类做个总结，需要注意，文章内容以算法和数据结构为中心，不考虑其他细节内容。如果小伙伴想看那个题目，可以直接跳转到（小测试）。

目录

• 一. 数据结构：queue[]、size、comparator
• 二. 初始化（堆化）：heapify()、siftDownComparable(k, e)
• 三. 添加元素：offer(e)、siftUpUsingComparator(k, e)
• 四. 索引：indexOf(o)
• 五. 删除元素：remove(o)、removeAt(i)、removeEq(o)
• 六. 取堆顶：peek()
• 七. 删除堆顶：poll()
• 八. 清除队列：clear()
• 九. 遍历：iterator()、toArray()、toArray(T[] a)
• 十. 小测试：数据流中的中位数

---

 一. 数据结构

我只列出了讲解需要的重要属性，不考虑其他细节。PriorityQueue（优先队列）内部是以堆来实现的。为了描述方便，接下来的内容我将用pq[ ]代替queue[ ]。

PriorityQueue<E> {
    /* 平衡二叉堆 用于存储元素
     * n : 0 -> size-1
     * pq[n].left = pq[2*n+1]
     * pq[n].right = pq[2*(n+1)]
     */
    Object[] queue; 
    int size; // pq中元素个数
    Comparator<? super E> comparator; // 自定义比较器
}

回到目录

二. 初始化（堆化）

如果使用已有集合来构造PriorityQueue，就会用到heapify()来对pq[ ]进行初始化（即：二叉堆化），使其满足堆的性质。而heapify()又通过调用siftDownComparable(k, e)来完成堆化。源码如下：

@SuppressWarnings("unchecked")
private void heapify() {
    final Object[] es = queue;
    int i = (size >>> 1) - 1;
    if (comparator == null)
        for (; i >= 0; i--)
            siftDownComparable(i, (E) es[i]);
    else
        for (; i >= 0; i--)
            siftDownUsingComparator(i, (E) es[i]);
}

@SuppressWarnings("unchecked")
private void siftDownComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>)x;
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
        int child = (k << 1) + 1; // assume left child is least
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        if (key.compareTo((E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = key;
}

如果有自定义比较器的话，调用：siftDownUsingComparator(k, e)，否则调用：siftDownComparable(k, e)。这两个方法只是在比较两个元素大小时的表现形式不同，其他内容相同，所以我们只需要看其中一种情况就行。为了描述方便，下面的例子中，我使用Integer作为pq[ ]存储元素类型，所以调用的是siftDownComparable(k, e)。（size >>> 1 表示 size 无符号右移1位，等价于size / 2）

我不会去细抠源码，一行一行地为大家讲解，而是尽量使用简单的例子来展示，我觉得通过例子以及后期大家自己阅读源码，会更容易理解算法内容。

现在我们来看看，使用集合{2, 9, 8, 4, 7, 1, 3, 6, 5}来构造PriorityQueue的过程。算法时间复杂度为O(n)，n = size。（时间复杂度证明：《算法导论》（第3版）第6章6.3建堆）

• 首先，从下到上，从右到左，找到第一个父结点 i，满足规律：i = (size >>> 1) - 1，这里size = 9，i = 3；
• 比较pq[3, 7, 8]中的元素，将最小的元素pq[x]与堆顶元素pq[3]互换，由于pq[x] = pq[3]，所以无互换；
• 移动到下一个父结点 i = 2，同理，比较pq[2, 5, 6]中的元素，将最小的元素pq[5]与pq[2]互换，后面的操作同理；
• 需要注意，当pq[1]（9）和pq[3]（4）互换后（如图2.d），pq[3, 7, 8]违背了最小堆的性质，所以需要进一步调整（向下调整），当调整到叶结点时（i >= size/2）结束；

回到目录

三. 添加元素

添加元素：add(e)，offer(e)，由于添加元素可能破坏堆的性质，所以需要调用siftUp(i, e)向上调整来维护堆性质。同样，siftUp(i, e)根据有无自定义比较器来决定调用siftUpUsingComparator(k, e)还是siftUpComparable(k, e)。在我举的例子中，使用的是siftUpComparable(k, e)。下面是添加元素的相关源码：

public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1);
    siftUp(i, e);
    size = i + 1;
    return true;
}

@SuppressWarnings("unchecked")
private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (key.compareTo((E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
}

源码中 grow(i + 1) 是当pq[ ]容量不够时的增长策略，目前可以不用考虑。现在来看往最小堆 pq = {3, 5, 6, 7, 8, 9} 中添加元素 1的过程。算法时间复杂度为O(lgn)，n = size。

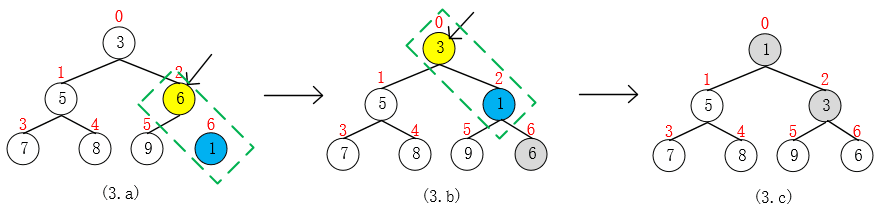
• 首先，把要添加的元素 1 放到pq[size]，然后调用siftUp(k, e)来维护堆，调整结束后 size++；
• 向上调整(k, e)时，先找到结点pq[k]的父结点，满足规律 parent = (k - 1) >>> 1，例子中，k = 6, parent = 2；
• 比较pq[k]与pq[parent]，将较小者放到高处，较大者移到低处，例子中，交换pq[6]（1）与pq[2]（6）的位置；
• 此次交换结束后，令 k = parent，继续以同样的方法操作，直到 k <= 0 时（到达根结点）结束；

回到目录

四. 索引

indexOf(o)是个私有方法，但好多公开方法中都调用了它，比如：remove(o)，contains(o)等，所以在这里也简单提一下。该算法并不复杂。时间复杂度为O(n)，n = size。

private int indexOf(Object o) {
    if (o != null) {
        for (int i = 0; i < size; i++)
            if (o.equals(queue[i]))
                return i;
    }
    return -1;
}

indexOf(o)中比较两个元素是否相等，使用的是equals()，而接下来要提的removeEq(o)中直接使用了 == 来判断，请读者注意区别。

回到目录

五. 删除元素

remove(o)、removeEq(o)，二者只是在判断两个元素是否相等时使用的方法不同（前者使用equals()，后者使用==），其他内容相同，它们都调用了removeAt(i)来执行删除操作。删除元素后很可能会破坏堆的性质，所以同样需要进行维护。删除元素的维护要比添加元素的维护稍微复杂一点，因为可能同时涉及了：向上调整siftUp和向下调整siftDown。源码如下：

public boolean remove(Object o) {
    int i = indexOf(o);
    if (i == -1)
        return false;
    else {
        removeAt(i);
        return true;
    }
}

boolean removeEq(Object o) {
    for (int i = 0; i < size; i++) {
        if (o == queue[i]) {
            removeAt(i);
            return true;
        }
    }
    return false;
}

@SuppressWarnings("unchecked")
E removeAt(int i) {
    // assert i >= 0 && i < size;
    modCount++;
    int s = --size;
    if (s == i) // removed last element
        queue[i] = null;
    else {
        E moved = (E) queue[s];
        queue[s] = null;
        siftDown(i, moved);
        if (queue[i] == moved) {
            siftUp(i, moved);
            if (queue[i] != moved)
                return moved;
        }
    }
    return null;
}

我们还是通过例子来学习吧，通过对 pq = {0, 1, 7, 2, 3, 8, 9, 4, 5, 6} 进行一系列删除操作，来理解算法的运作过程。算法时间复杂度O(lgn)，n = size。

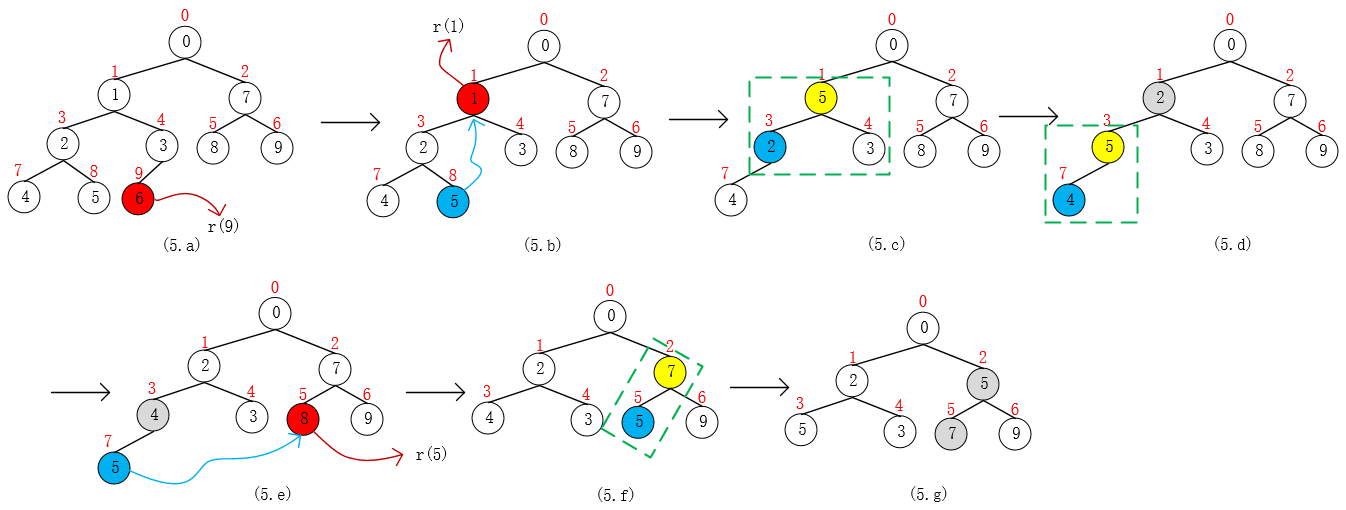
• 第1步，remove(6)，indexOf(6) = 9，removeAt(9)（用r(9)表示，后面同理）,由于i = 9为队列末端，删除后不会破坏堆性质，所以可以直接删除；
• 第2步，remove(1)，即r(1)，根据图(5.b)可以看出，算法是拿队列尾部pq[8]去替换pq[1]，替换后破坏了最小堆的性质，需要向下调整进行维护；
• 第3步，remove(8)，即r(5)，使用队列尾部元素pq[7]替换pq[5]，替换后破坏了最小堆的性质，需要向上调整进行维护；

回到目录

六. 取堆顶

peek()可以在O(1)的时间复杂度下取到堆顶元素pq[0]，看源码一目了然：

@SuppressWarnings("unchecked")
public E peek() {
    return (size == 0) ? null : (E) queue[0];
}

回到目录

七. 删除堆顶

删除堆顶使用poll()方法，其算法思想等价于removeAt(0)（时间复杂度O(lgn)），稍微有点区别的是，其只涉及到向下调整，不涉及向上调整。不清楚的朋友可以参看（五. 删除元素），下面是源码：

@SuppressWarnings("unchecked")
public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x);
    return result;
}

回到目录

八. 清除队列

清除队列clear()，就是依次把pq[i]置为null，然后size置0，但是pq.length没有改变。时间复杂度为O(n)，n = size。源码如下：

public void clear() {
    modCount++;
    for (int i = 0; i < size; i++)
        queue[i] = null;
    size = 0;
}

回到目录

九. 遍历

可以使用迭代器（Iterator）来遍历pq[ ]本身，或者调用toArray()、toArray(T[] a)方法来生成一个pq[ ]的副本进行遍历。遍历本身的时间复杂度为O(n)，n = size。

使用迭代器遍历 pq = {0, 1, 7, 2, 3, 8, 9, 4, 5, 6}，方法如下：

public static void traverse1(PriorityQueue<Integer> x) {
    Iterator<Integer> it = x.iterator();
    while (it.hasNext()) {
        System.out.print(it.next() + " ");
    }
    System.out.println();
}
// 或者更简单的，结合java语法糖，可以写成如下形式
public static void traverse2(PriorityQueue<Integer> x) {
    for (int a : x) {
        System.out.print(a + " ");
    }
    System.out.println();
}
/* 输出
0 1 7 2 3 8 9 4 5 6 
*/

通过拷贝pq[ ]副本来遍历，方法如下：

public static void traverse3(PriorityQueue<Integer> x) {
    Object[] ins = x.toArray();
    for (Object a : ins) {
        System.out.print((Integer)a + " ");
    }
    System.out.println();
}

public static void traverse4(PriorityQueue<Integer> x) {
    Integer[] ins = new Integer[100];
    ins = x.toArray(ins);
    for (int i = 0, len = x.size(); i < len; i++) {
        System.out.print(ins[i] + " ");
    }
    System.out.println();
}
/* 输出
0 1 7 2 3 8 9 4 5 6 
*/

在使用toArray(T[] a)拷贝来进行遍历时，需要注意（x表示PriorityQueue对象）：

• 如果ins[ ]的容量大于x.size()，请使用for (int i = 0; i < x.size(); i++) 来遍历，否则可能会获取到多余的数据；或者你使用for (int a : ins)来遍历时，可能导致NullPointerException异常；
• 请使用 ins = x.toArray(ins) 的写法来确保正确获取到pq[ ]副本。当ins[ ]容量大于x.size()时，写为 x.toArray(ins) 能正确获取到副本，但当ins[ ]容量小于x.size()时，该写法就无法正确获取副本。因为此情况下toArray(T[] a)内部会重新生成一个大小为x.size()的Integer数组进行拷贝，然后return该数组；

toArray(T[] a)源码如下：

@SuppressWarnings("unchecked")
public <T> T[] toArray(T[] a) {
    final int size = this.size;
    if (a.length < size)
        // Make a new array of a's runtime type, but my contents:
        return (T[]) Arrays.copyOf(queue, size, a.getClass());
    System.arraycopy(queue, 0, a, 0, size);
    if (a.length > size)
        a[size] = null;
    return a;
}

回到目录

十. 小测试

下面来说说文章开头我提到的那个题目吧，如下（点击这里在线做题）（请使用PriorityQueue来完成）：

/* 数据流中的中位数
题目描述
如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。
如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，
使用GetMedian()方法获取当前读取数据的中位数。
*/

public class Solution {
    public void Insert(Integer num) {}
    public Double GetMedian() {}
}

我写的参考代码（带解析），如下：

/*
关键点：
 大根堆maxq       小根堆minq
----------      -------------
          \    /
  <= A     A  B   >= B
          /    \
----------      -------------
 
每次insert(num)前要确保 ：
    1) maxq.size == q.size // 偶数个时，二者元素个数相等
或  2) minq.size == maxq.size + 1 // 奇数个时把多余的1个放到小根堆minq
这样一来，获取中位数时：
奇数个：minq.top;
偶数个：(minq.top + maxq.top) / 2
 
每次isnert(num)后，可能会打破上面的条件，出现下面的情况：
    1) maxq.size == q.size + 1 // 打破条件(1) => 这时需要把maxq.top放到minq中
或  2) minq.size == maxq.size + 2 // 打破条件(2) => 这时需要把minq.top放到maxq中
*/

import java.util.Comparator;
import java.util.PriorityQueue;
 
public class JZOffer_63_Solution_02 {
    PriorityQueue<Integer> minq = new PriorityQueue<Integer>();
    PriorityQueue<Integer> maxq = new PriorityQueue<Integer>((o1, o2) -> o2.compareTo(o1));

    public void Insert(Integer num) {
        if (minq.isEmpty() || num >= minq.peek()) minq.offer(num);
        else maxq.offer(num);
        if (minq.size() == maxq.size()+2) maxq.offer(minq.poll());
        if (maxq.size() == minq.size()+1) minq.offer(maxq.poll());
    }

    public Double GetMedian() {
        return minq.size() == maxq.size() ? (double)(minq.peek()+maxq.peek())/2.0 : (double)minq.peek();
    }
}

回到目录

 转载请说明出处，have a good time! :D