09-堆 Heap(最大堆)
学习资源:慕课网liyubobobo老师的《玩儿转数据结构》
1、堆
1.1、二叉堆
-
是一棵完全二叉树。完全二叉树:简单理解,就是把元素按从左到右的顺序,一层一层地排列成二叉树的形状
-
有两种二叉堆:
-
最大堆
-
最小堆
-
1.2、最大堆
满足:堆中某个结点的值总是不大于其父结点的值
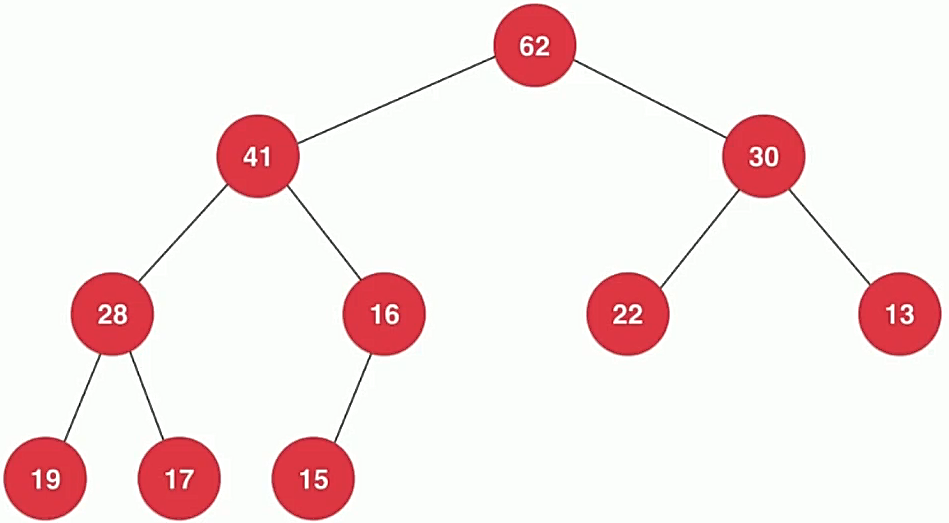
1.3、最小堆
满足:堆中某个结点的值总是不大于其孩子结点的值
2、最大堆的实现
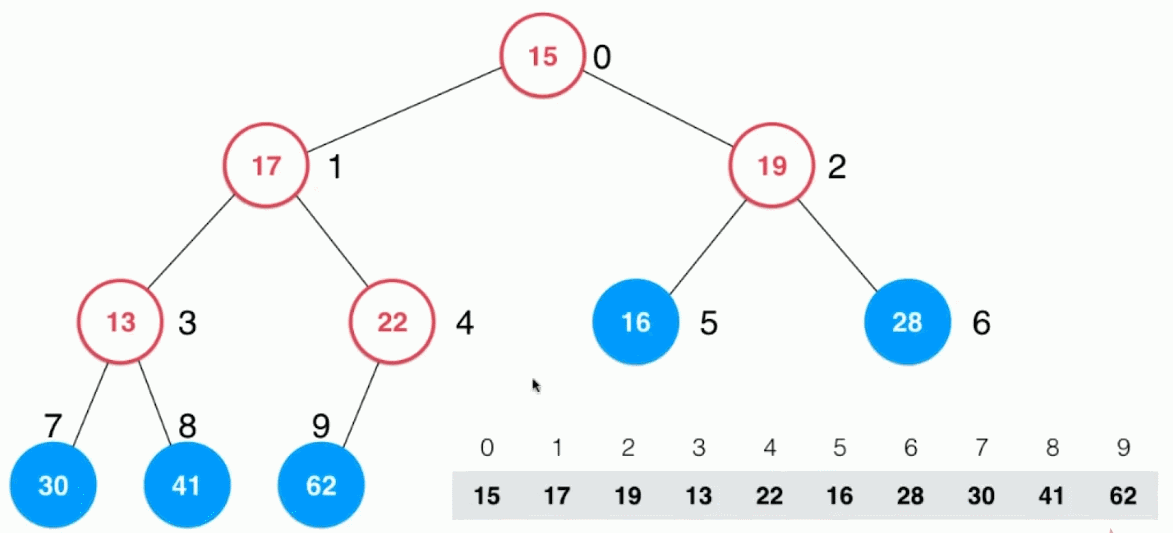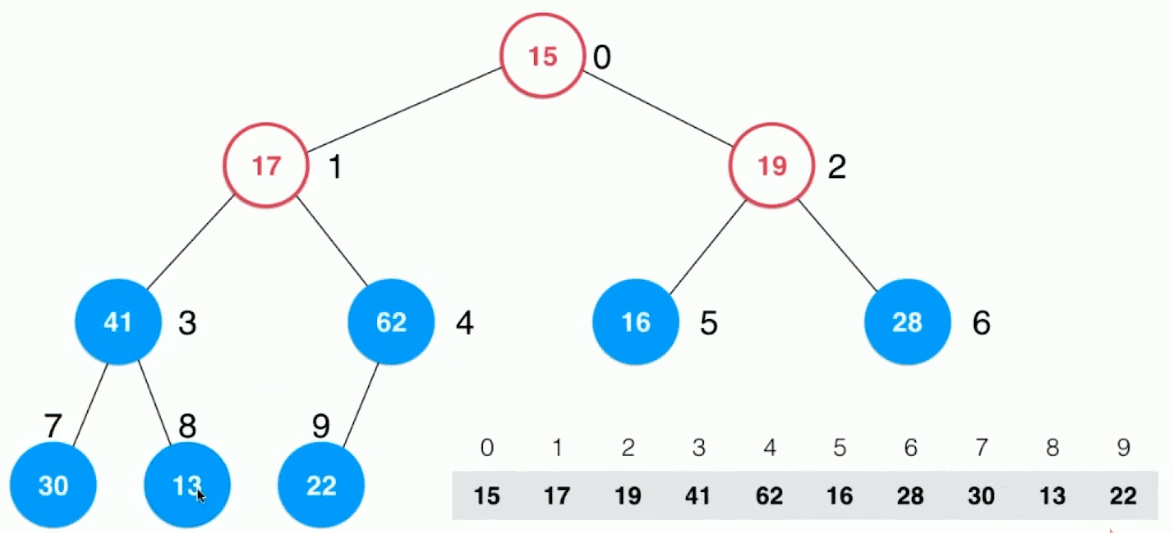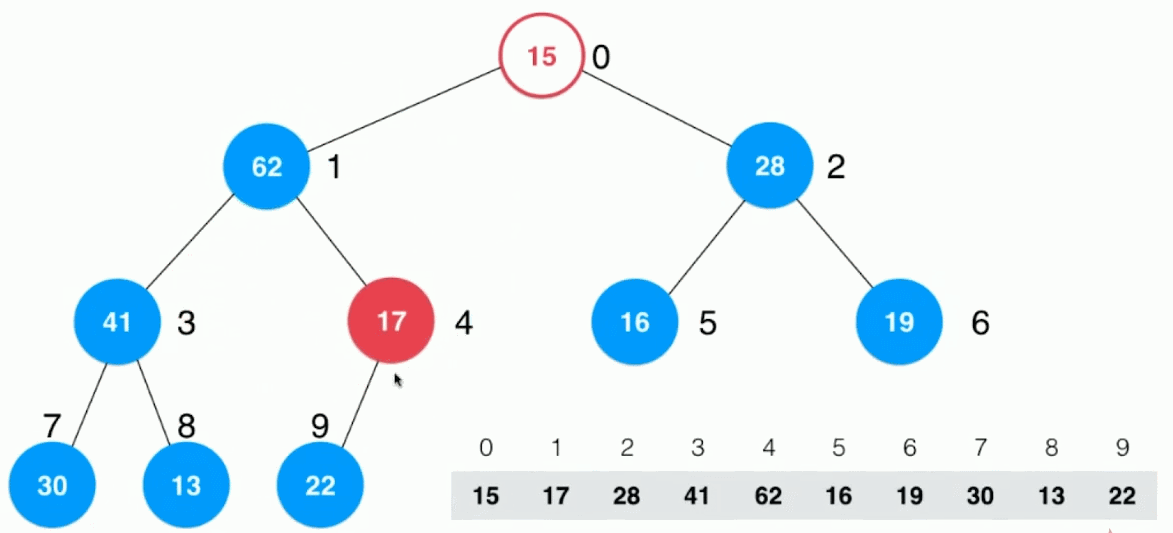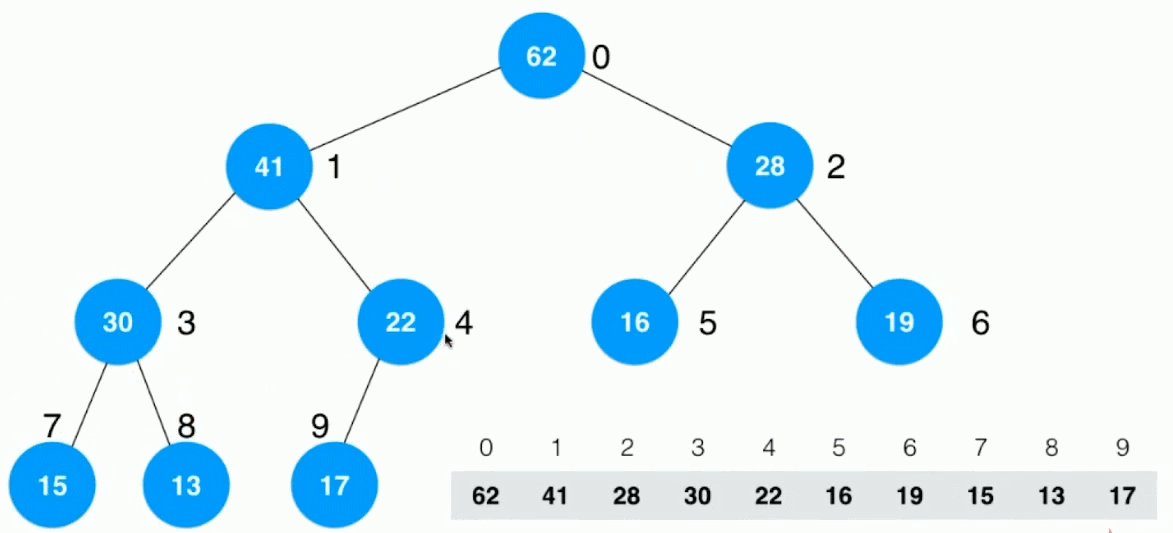
可以使用数组表示一棵完全二叉树。完全二叉树逐层从左到右使用数字标记每个结点,数字对应数组中的索引。
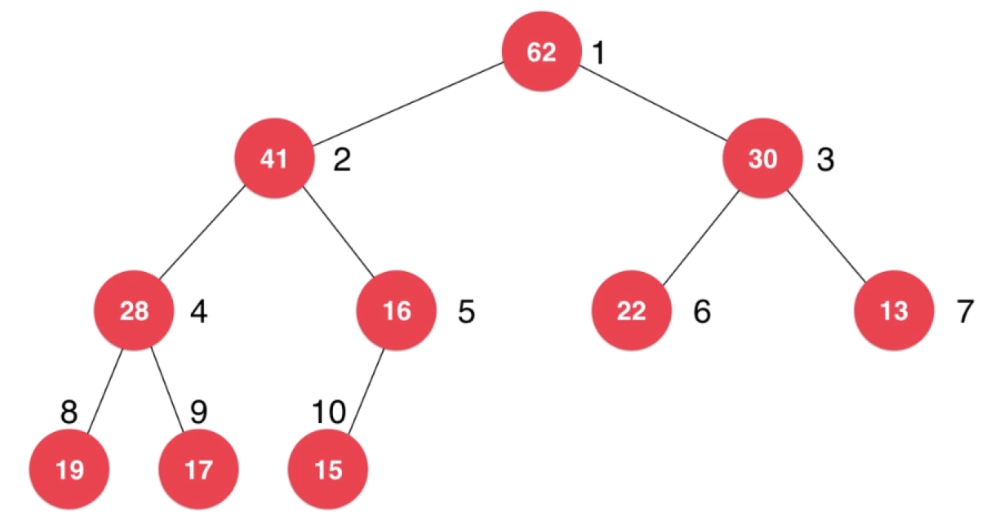
最大堆的内部使用数组实现,但对外展示还是使用完全二叉树的形式。
2.1、实现方式
2.1.1、方式一
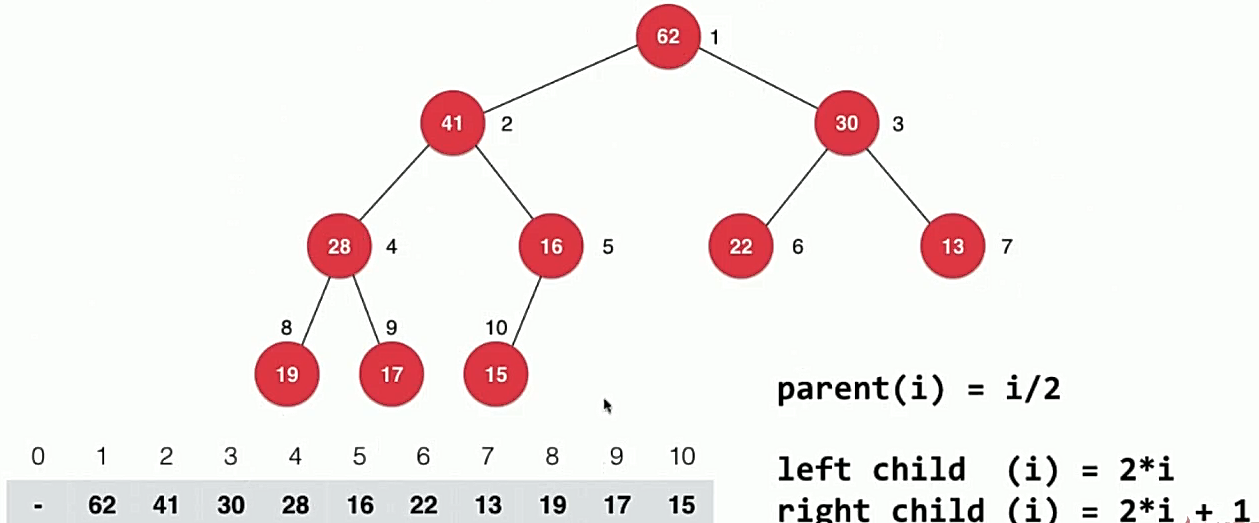
索引从 1 开始,0 空出,结点的索引有以下规律:
- 结点 i 的父结点:
parent(i) = i/2(向下取整) - 结点 i 的左孩子结点:
leftChild(i) = 2*i - 结点 i 的右孩子结点:
rightChild(i) = 2*i + 1
2.1.2、方式二
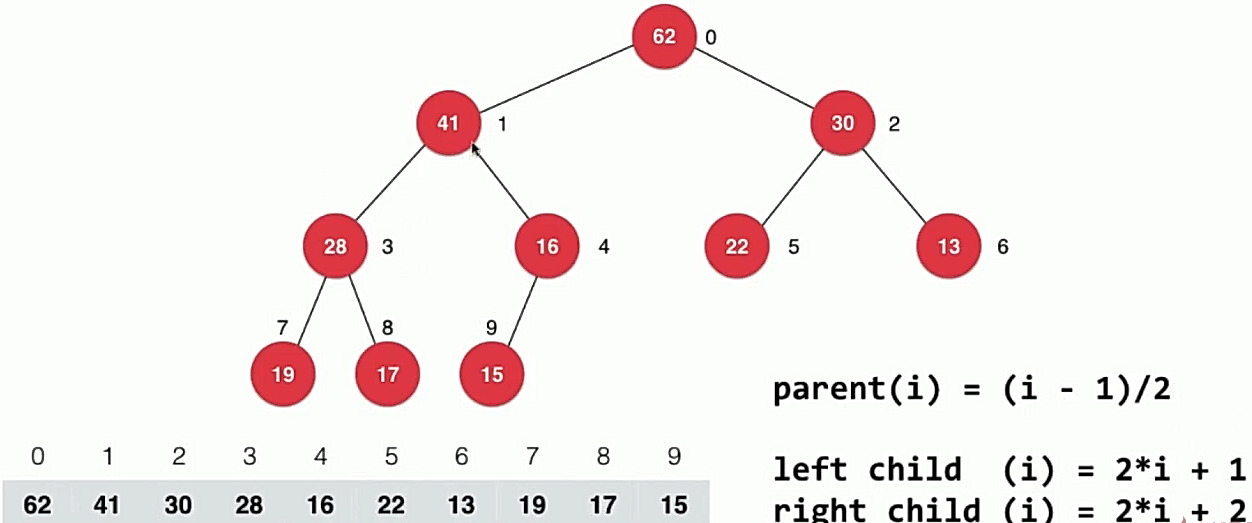
索引从 0 开始,结点的索引有以下规律:
- 结点 i 的父结点:
parent(i) = (i - 1)/2(向下取整) - 结点 i 的左孩子结点:
leftChild(i) = 2*i + 1 - 结点 i 的右孩子结点:
rightChild(i) = 2*i + 2
2.2、代码实现
2.2.1、基础部分
package heap;
import array.Array;
// 根结点索引从 0 开始
public class MaxHeap<E extends Comparable<E>> {
//基于动态数组
private Array<E> data;
public MaxHeap(int capacity) {
data = new Array<>(capacity);
}
public MaxHeap() {
data = new Array<>();
}
public int size(){
return data.getSize();
}
public boolean isEmpty(){
return data.isEmpty();
}
private int parent(int index){
if(index == 0){
throw new IllegalArgumentException("根结点没有父结点");
}
return (index - 1)/2;
}
private int leftChild(int index){
return index*2 + 1;
}
private int rightChild(int index){
return index*2 + 2;
}
}
在之前实现的动态数组中添加一个API
// 交换两个索引处的值
public void swap(int i, int j){
if(i<0 || i>=size || j<0 || j>=size)
throw new IllegalArgumentException("索引越界");
E e = data[i];
data[i] = data[j];
data[j] = e;
}
2.2.2、添加结点 和 Sift Up
在堆的内部,元素是存储在数组中的,所以很容易实现添加操作;但是添加后操作完成之后,还要根据最大堆的性质进行调整。
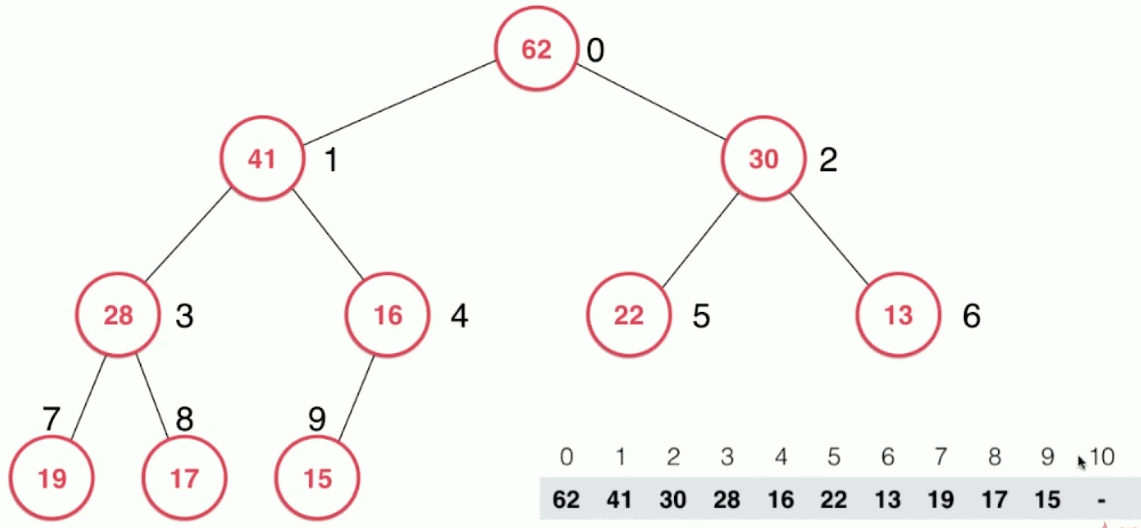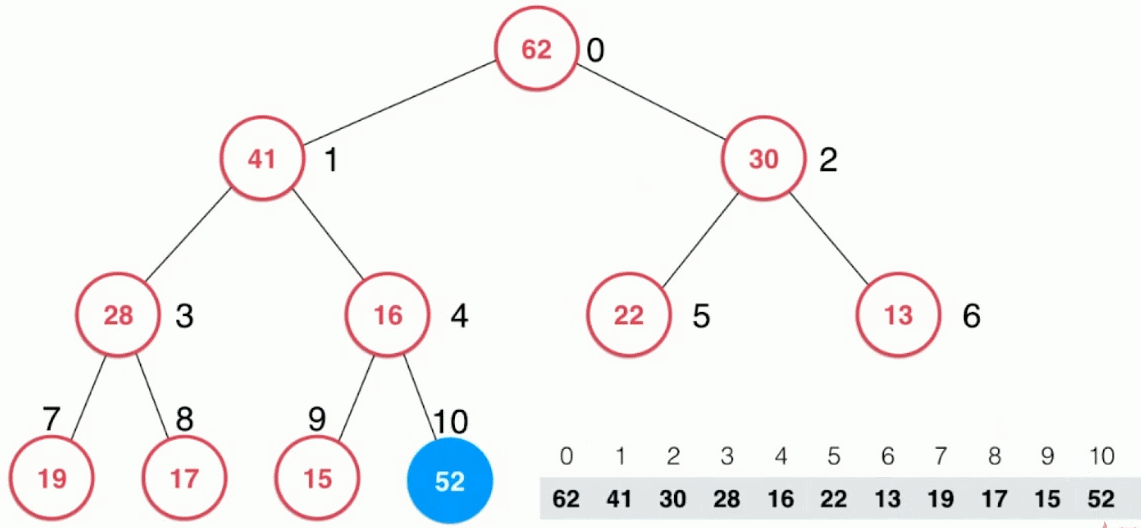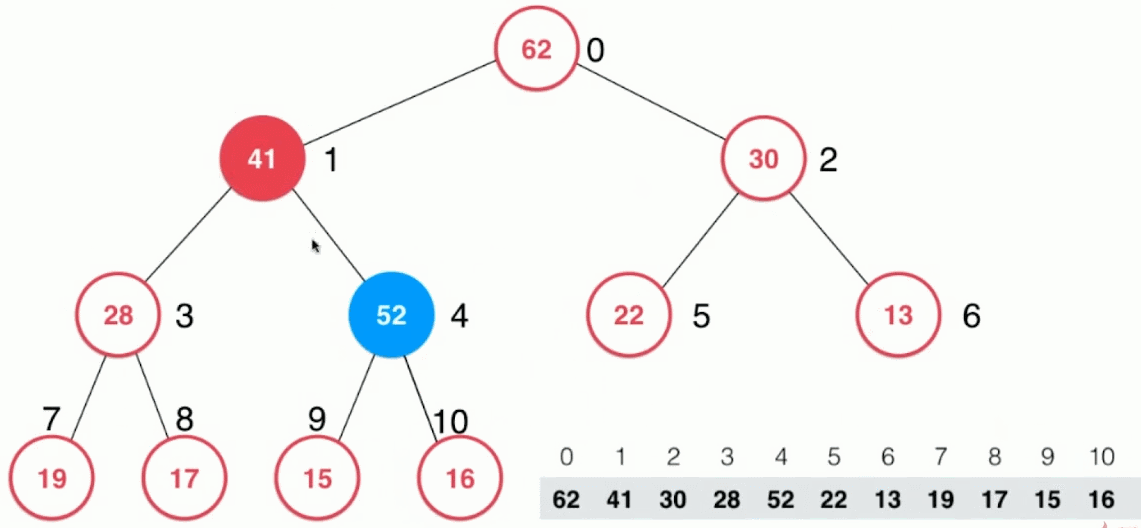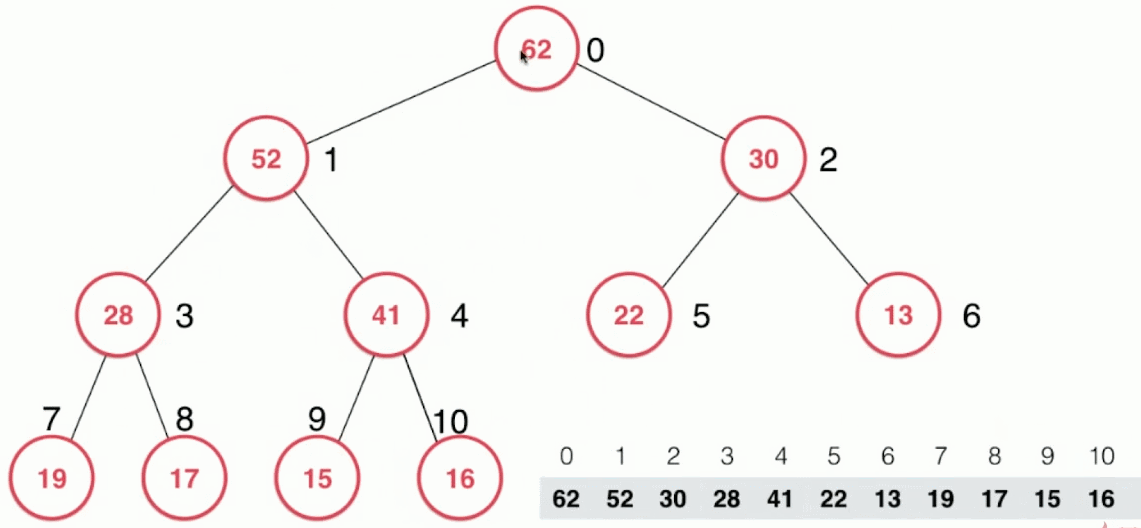
实现思路:
- 将新添加的结点与其父结点进行比较,如果不满足最大堆的性质,交换新添加结点和父结点的位置即可(在数组中是比较容易实现的)
- 重复上述比较交换的过程,直到新添加的结点小于其当前的父结点
// 添加元素
public void add(E e){
data.addToLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k) {
while (k > 0 && data.get(k).compareTo(data.get(parent(k))) > 0){
data.swap(k, parent(k));
//继续判断交换后的新结点是否大于现在的父结点
k = parent(k);
}
}
2.2.3、取出元素 和 Sift Down
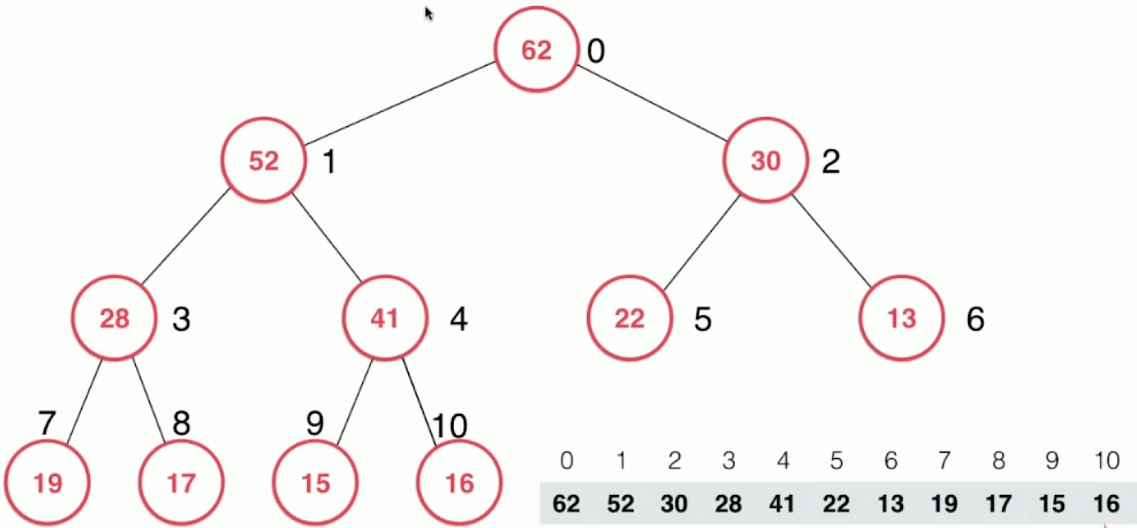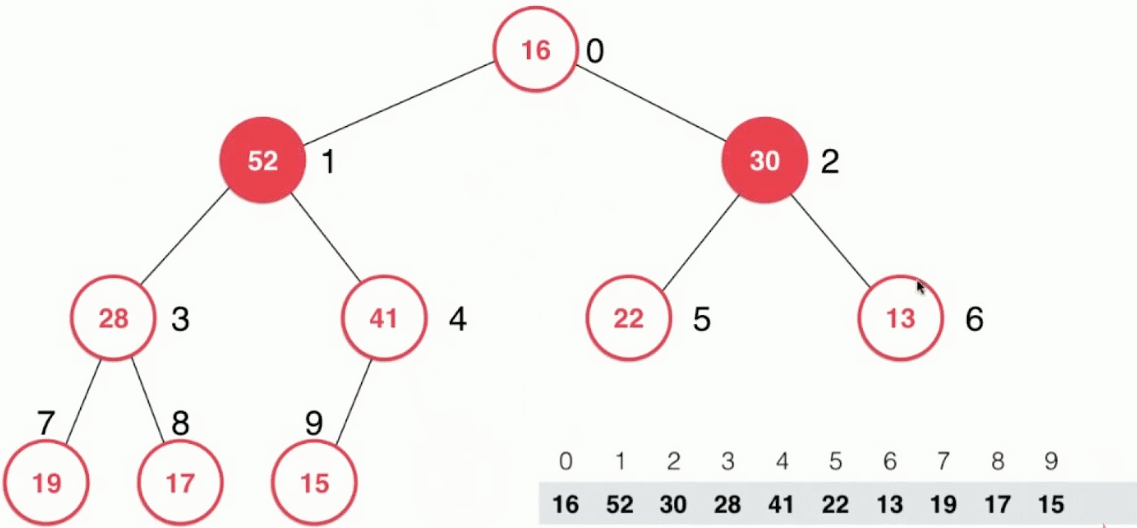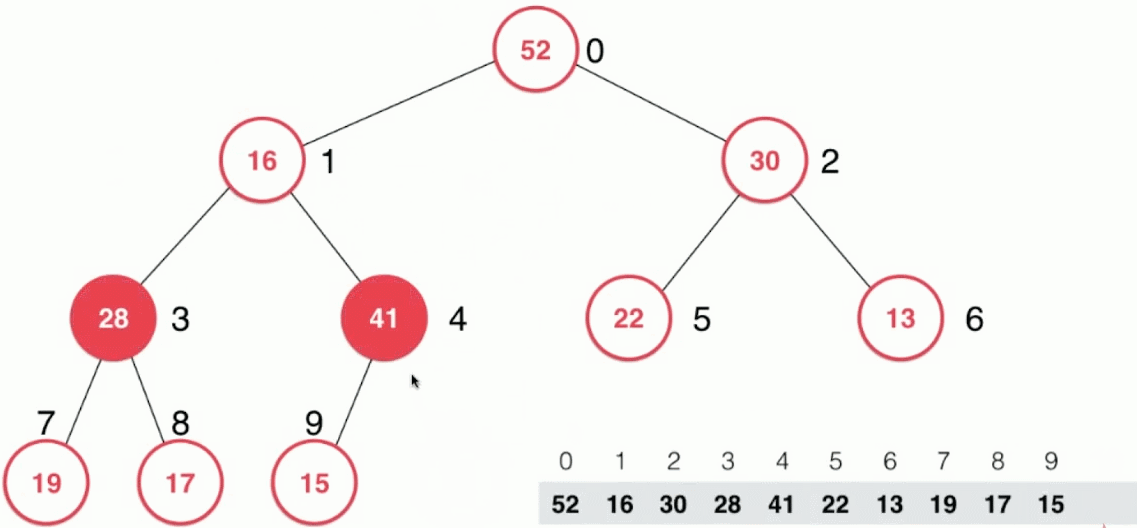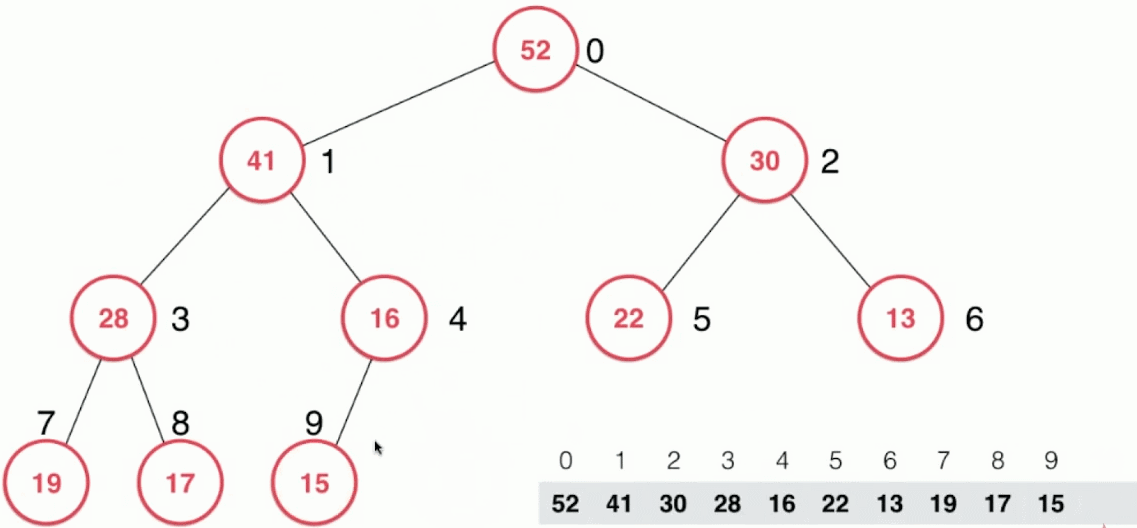
对于最大堆,取出元素时只取出最大元素,即堆顶得结点,也即数组的第一个元素。
实现思路:
- 取出最大元素62后,将数组中的最后一个元素16放置到堆顶
- 然后进行调整:新的堆顶结点16和其左右孩子结点比较,并与其中最大的孩子结点52交换位置
- 然后再向下不断进行,直到16这个结点到达合适的位置
// 查看堆中的最大元素
public E findMax(){
if(data.getSize() == 0){
throw new IllegalArgumentException("堆为空,没有最大结点");
}
return data.get(0);
}
// 取出堆中的最大元素
public E exactMax(){
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
private void siftDown(int k) {
while(leftChild(k) < data.getSize()){
// 找到结点k 的左右孩子中最大的结点
int maxChild = leftChild(k);
//右孩子 > 左孩子
if(maxChild+1 < data.getSize() && data.get(maxChild+1).compareTo(data.get(maxChild)) > 0){
maxChild = rightChild(k);
}
// 如果结点k已经满足最大堆,退出循环即可
if(data.get(k).compareTo(data.get(maxChild)) >=0){
break;
}
data.swap(k, maxChild);
k = maxChild;
}
}
2.2.4、replace
定义:取出最大元素后,放入一个新元素;也相当于将最大元素替换为新元素
实现思路(这里选择思路2):
- 可以先
extractMax,再add, 两次O(logn)的操作 - 也可以直接将堆顶元素替换为新元素,再对堆顶元素Sift Down,一次O(logn)的操作
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
2.2.5、heapify
定义:将任意数组整理成堆的形状
实现思路:
-
通过循环将数组中的元素逐个添加进堆对象中。复杂度为O(nlogn)
-
从最后一个非叶子结点(最后一个结点的父结点),从下之上、从右至左(对应到数组中也就是从后向前),逐个地对每一个元素元素进行Sift Down。复杂度为O(n)
-
直到对根结点完成 Sift Down
在Array类中添加新的构造器函数,传入一个静态数组转换为动态数组
public Array(T[] arr){
data = (T[])new Object[arr.length];
for(int i=0; i<arr.length; i++){
data[i] = arr[i];
}
size = arr.length;
}
public MaxHeap(T[] arr){
data = new Array<>(arr);
for (int i = parent(arr.length-1); i >=0 ; i--) {
siftDown(i);
}
}
3、全部代码
package heap;
import array.Array;
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity) {
data = new Array<>(capacity);
}
public MaxHeap() {
data = new Array<>();
}
public MaxHeap(E[] arr){
data = new Array<>(arr);
for (int i = parent(arr.length-1); i >=0 ; i--) {
siftDown(i);
}
}
public int size(){
return data.getSize();
}
public boolean isEmpty(){
return data.isEmpty();
}
private int parent(int index){
if(index == 0){
throw new IllegalArgumentException("根结点没有父结点");
}
return (index - 1)/2;
}
private int leftChild(int index){
return index*2 + 1;
}
private int rightChild(int index){
return index*2 + 2;
}
// 添加元素
public void add(E e){
data.addToLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k) {
while (k > 0 && data.get(k).compareTo(data.get(parent(k))) > 0){
data.swap(k, parent(k));
//继续判断交换后的新结点是否大于现在的父结点
k = parent(k);
}
}
// 查看堆中的最大元素
public E findMax(){
if(data.getSize() == 0){
throw new IllegalArgumentException("堆为空,没有最大结点");
}
return data.get(0);
}
// 取出堆中的最大元素
public E exactMax(){
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
private void siftDown(int k) {
while(leftChild(k) < data.getSize()){
// 找到结点k 的左右孩子中最大的结点
int maxChild = leftChild(k);
//右孩子 > 左孩子
if(maxChild+1 < data.getSize() && data.get(maxChild+1).compareTo(data.get(maxChild)) > 0){
maxChild = rightChild(k);
}
// 如果结点k已经满足最大堆,退出循环即可
if(data.get(k).compareTo(data.get(maxChild)) >=0){
break;
}
data.swap(k, maxChild);
k = maxChild;
}
}
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
}
4、测试
测试Sift Down,从最大堆中取出元素,其输出必然保证有序
@Test
public void test(){
int n = 100;
MaxHeap<Integer> heap = new MaxHeap<>();
Random random = new Random();
for(int i = 0; i<n; i++){
heap.add(random.nextInt(Integer.MAX_VALUE));
}
int[] arr = new int[n];
for (int i = 0; i <n; i++) {
arr[i] = heap.exactMax();
}
for (int i = 1; i < n; i++) {
// System.out.println(arr[i-1]);
if(arr[i-1] < arr[i]){
throw new RuntimeException("堆错误");
}
}
System.out.println("堆正确");
}
5、其他类型的堆
- d叉堆
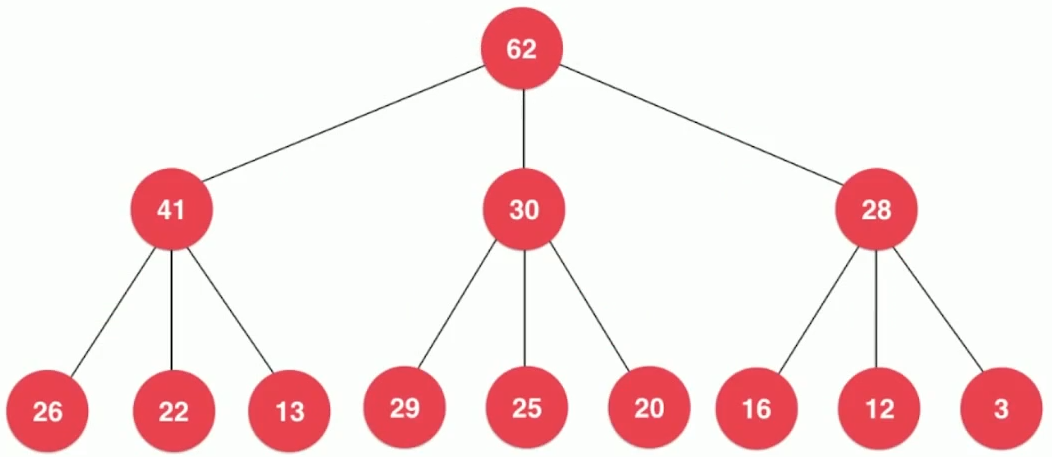
- 索引堆
- 二项堆
- 斐波那契堆
6、基于最大堆的优先队列
优先队列:在优先队列中,元素被赋予优先级;当访问元素时,具有最高优先级的元素最先出队。
底层直接复用最大堆的方法实现队列的接口即可
package heap;
import queue.arrayQueue.Queue;
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
private MaxHeap<E> maxHeap;
public PriorityQueue() {
this.maxHeap = new MaxHeap<>();
}
@Override
public void enqueue(E e) {
maxHeap.add(e);
}
@Override
public E dequeue() {
return maxHeap.exactMax();
}
@Override
public E getFront() {
return maxHeap.getMax();
}
@Override
public int getSize() {
return maxHeap.size();
}
@Override
public boolean isEmpty() {
return maxHeap.isEmpty();
}
}
7、Java中的优先队列
PriorityQueue,底层是最小堆
特点:构造器可以传入一个比较器,规定优先级
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
}
API接口