树形 DP 专题
树形 DP 专题
P9584 「MXOI Round 1」城市#
题目大意#
给定一个 个节点的树,边有边权,以及 次相互独立的询问,每次询问给定 ,意义为在 号节点和 号节点之间连一条长度为 的边。强制在线。问操作之后,树上所有路径的权值和之和,即:
Solve#
略。见口胡。
Code#
void dfs(int x,int ffa,int val){
siz[x] = 1, res = (res + val) % mod;
for(auto [y, v] : ed[x]){
if(y == ffa) continue;
dfs(y, x, val + v);
siz[x] += siz[y];
}
return;
}
void dfs1(int x,int ffa,int cnt){
V[x] = (cnt + mod) % mod;
if(x != 1) res = (res + cnt) % mod;
for(auto [y, v] : ed[x]){
if(y == ffa) continue;
dfs1(y, x, cnt + n * v % mod - 2ll * siz[y] % mod * v % mod);
}
return;
}
signed main()
{
cin >> n >> q;
for(int i = 1; i < n; ++i){
int st,en,val;
scanf("%lld%lld%lld",&st,&en,&val);
ed[st].push_back({en, val});
ed[en].push_back({st, val});
}
dfs(1, 0, 0);
dfs1(1, 0, res);
res = (res + mod) % mod;
while(q--){
int x,v;
scanf("%lld%lld",&x,&v);
printf("%lld\n",((((n * v % mod + V[x]) * 2ll % mod + res) % mod) + mod) % mod);
}
return 0;
}
P3262 [JLOI2015] 战争调度#
题目大意#
给定一棵 层的完全二叉树,第 号节点的儿子编号为 和 。给每个点钦定状态为 0/1,记为 。钦定完每个点的状态后,整棵树的价值定义为:
其中, 是给定的。求任意钦定,整棵树的最大价值,要求叶子节点的 1 的个数不超过 。。
Solve#
考虑一个暴力的状压 DP:记 表示仅 的子树, 的祖先链状态是 ,叶子节点选了 个 1 的最大价值。转移比较简单,只是在朴素树背包的基础上加了一个枚举状态。时空复杂度似乎是 ,约 ,不能通过。时间上可以卡一卡,但空间上是完全开不下的。
但是考虑, 对于一个节点 ,它的 的范围不一定是严格的 ,所以这个复杂度不是很真。由此我们考虑不把 记录在 中,而是在 dfs 时作为参数记录,对于每一种祖先链状态都去跑一遍树背包。空间复杂度 ,我们分析一下时间复杂度。
考虑对于一个在第 层的点,它会被遍历到 次,即把上面 层祖先链的状态都枚举一遍。而第 层的点有 个。如果把每个点每一次被遍历到时,都认为它被复制了一遍,那么最后仍然是一棵树,且点数为:
等比数列求和,化简后为 。
再套一个树背包,所以总复杂度为 ,约 ,且极松,可以通过。
Code#
void dfs(int u,int s,int siz/*当前子树内叶节点个数*/)
{
for(int i=0;i<=siz;i=-~i) f[u][i]=0;
if(u>=(n>>1))//叶节点
{
f[u][1]=f[u][0]=0;
for(int i=0;i<dep-1;i=-~i)
f[u][s>>i&1]+=a[s>>i&1][u][i];
return;
}
for(int t=0;t<2;t=-~t)
{
dfs(u<<1,s<<1|t,siz>>1);dfs(u<<1|1,s<<1|t,siz>>1);
for(int i=0;i<=m&&i<=(siz>>1);i=-~i)//树背包
for(int j=0;i+j<=m&&j<=(siz>>1);j=-~j)
f[u][i+j]=max(f[u][i+j],f[u<<1][i]+f[u<<1|1][j]);
}
}
signed main()
{
dep=read();m=read();n=1<<dep;
for(int t=1;-~t;t=~-t)
for(int i=n>>1;i<n;i=-~i)
for(int j=0;j<dep-1;j=-~j)
a[t][i][j]=read();
dfs(1,0,n>>1);
for(int i=0;i<=m;i=-~i) ans=max(ans,f[1][i]);
return printf("%d",ans),0;
}
P4516 [JSOI2018] 潜入行动#
题目大意#
选择恰好个点使得这些点的临域覆盖所有点。
比较经典的树形 dp,我们设 表示以 为根的子树内选了 个点, 这个点选或不选,有没有被覆盖。
转移采用将两颗子树合并的方式,分情况讨论:
-
对于 ,此时这个点没有被选,且没有被覆盖,只需要保证儿子已经被覆盖。所以有:
-
对于 ,如果这个点一开始没被覆盖,更新后被覆盖,只能是选了儿子并且因为这个点没有选,所以要保证儿子必须已经被覆盖;而如果这个点一开始被覆盖了,不用关心儿子是否被选,只需考虑儿子必须被覆盖。所以有:
-
对于 ,这个时候选择了 ,儿子不用担心是否被覆盖,但是第 维 的限制要求儿子不能被选,所以有:
-
对于 ,如果 之前没被覆盖,那么要求儿子一定要选,否则的话可以从儿子所有状态转移而来。那么有:
最后注意一点小细节,就是自己可能会给自己转移,所以转移时最好再开一个数组存一下修改前的 dp 值就好了。
还有 数组直接开 long long 会炸空间,所以开 int 在转移过程中强制转化就好了。
Code#
HERE。
我们在枚举选点转移的时候理论复杂度看起来像是 的。但是,我们发现这个形式是树背包的形式,那么只要实现的好,复杂度实际上是 的。证明见此。
P8867 [NOIP2022]建造军营#
题目大意#
见题目描述:[NOIP2022]建造军营
Solve#
首先,如果对于一个边双,断开任意一条道路,一定能从另外一条道路走到这个点,所以说直接缩点,缩完点后一个连通块内的贡献就是 ,缩完点之后就得到了一棵树。然后考虑树形 dp 。
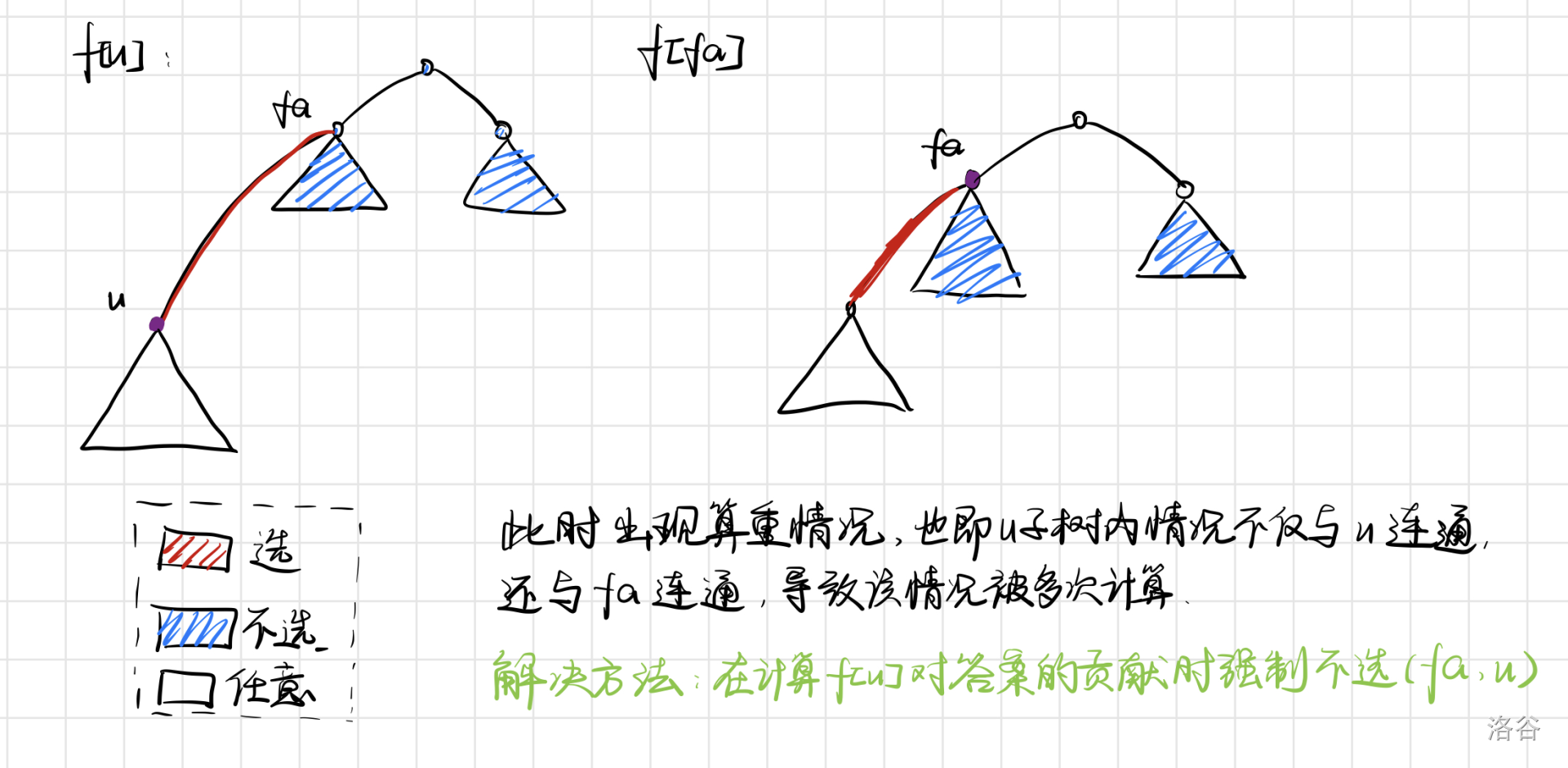
设状态 表示以 为根的子树中没有有军营的总方案数,并且如果第二维是 的话,那么钦定 点和其儿子之间的边必选。
假设一个边双里的点数为 ,边数为 ,那么转移有:
其中, 的初值是 。
Code#
好水的题解
P6803 [CEOI2020] 星际迷航#
题目大意#
给定一颗 个节点的树。这样的树有 层,编号从 到 。对于 ,需要选择第 层的任意一个节点向第 层的任意一个节点连一条有向边。最初人在第 层图的 号节点。两个玩家交替选择下一步向哪走,要求走到的点 之前没有到过,且与当前节点 相邻或有一条有向边从 指向 。如果到一个玩家选择时,不能走到任何没有到过的节点,这个玩家就输了。问有多少种连有向边的方案能使得先手必胜。
Solve#
首先,如果从一棵树的节点 开始走,那么将这棵树的根定为 之后,走出的合法路径一定是一条从浅往深走的链。所以如果第 层和第 层间的有向边指向节点 ,那么相当于把第 层的树的根定为 。
连接这条有向边之后,会根据节点 是必胜还是必败,对这条边起点的状态做出一定修改。所以,我们并不关心这条有向边指向的是哪个节点,只关心从指向的那个节点开始,先手是必胜还是必败。
由此,我们设计如下状态:设 表示考虑了 层树,从第 1 棵树的任意节点开始走,使得先手必胜 / 必败,这样的连边的总方案数。
考虑我把在这 层树前面再添一层树(记为第 0 棵树),即把原来的第 1 棵树连在第 0 棵的某个节点下。 如何转移到 ?
记新连的这条有向边为 。第 棵树的根为 。
对于 ,我要求最后先手必胜。
- 如果 原本是必胜的,我要求 不能改变 的状态;
- 否则,我要求必须改变 的状态。
对于 ,类似。
接下来考虑什么样的 能使 的状态发生改变。显然当这 层树在从 开始时是必胜态时, 一定不会改变 的状态,即: 只有连向一个必败点, 才会改变 的状态。
所以我们设 表示在以 为根时,有多少个节点 满足从 向一个必败点连边后, 的状态会发生改变。
如果求出来 ,我们根据 原本的状态和要转移到的状态的异同,就能知道是否要求 必须改变 的状态,就有了如下状态转移式:
其中, 表示在原树中,以 为根是先手必胜还是必败。 为这 层间的总连边方案。
系数为定值,并且 的范围很大,但第二维状态很少,所以考虑矩阵快速幂加速。
求出 之后,根据 来计算最终答案即可。
的换根比较简单。问题是 怎么求。
先考虑若以 1 为根,如何求 ,即朴素树形 dp。
设 表示以 为根时, 的子树内有多少节点满足向必败点连边后能改变 的状态。分情况讨论。
- 若 子树内必败,那么 即为所有儿子 的和,再加上 1,即自己直接连向必败点的方案。
- 否则若 的儿子里只有一个必败,那个儿子记为 ,那么 。
至于换根,记 表示以 为根时, 儿子里必败 / 必胜点的 值的和, 表示以 为根时, 儿子里必败 / 必胜点的 值的和。那么 的转移可以形式化地表示为:
其中, 表示以 1 为根时, 的儿子内必败点个数。之所以弃掉原本必胜 / 必败的意义,是为了方便转移。
接下来考虑如何换根求 。
当根从 换到 时,首先要把 的贡献从 里刨掉得到 ,之后根据上面的式子,计算 ,用 更新 。
感觉重点在这个 的定义,很巧妙,省去了很多讨论。
Code#
void F(int u,int fa)
{
for(int v:e[u])
if(v!=fa)
F(v,u),h[u]+=!h[v],w[u][h[v]>0]+=g[v];
if(h[u]==1) g[u]=w[u][0];
if(!h[u]) g[u]=w[u][1]+1;
}
void G(int u,int fa)//换根
{
if(!h[u]) cnt=-~cnt;
int _h,_g,_w[2];//把某个儿子刨去后的相应值
for(int v:e[u])
if(v!=fa)
{
_w[0]=w[u][0],_w[1]=w[u][1];
_h=h[u]-!h[v];_w[h[v]>0]-=g[v];
if(_h>1) _g=0;
else if(_h) _g=_w[0];
else _g=_w[1]+1;
h[v]+=!_h;w[v][_h>0]+=_g;
if(h[v]>1) g[v]=0;
else if(h[v]) g[v]=w[v][0];
else g[v]=w[v][1]+1;
G(v,u);
}
}
struct mat{矩乘板子}a;
signed main()
{
n=read();m=read();
for(int i=1,u,v;i<n;i=-~i)
u=read(),v=read(),
e[u].push_back(v),e[v].push_back(u);
F(1,0);G(1,0);
for(int i=1;i<=n;i=-~i)//根据换根求得的 g 计算转移矩阵
if(h[i])
add(a.a[0][0],g[i]),
add(a.a[0][1],n-g[i]),add(a.a[1][1],n);
else
add(a.a[0][1],g[i]),
add(a.a[0][0],n-g[i]),add(a.a[1][0],n);
a=a^(m-1);
int x=(1ll*cnt*a.a[0][0]+1ll*(n-cnt)*a.a[1][0])%MOD;
int y=(1ll*cnt*a.a[0][1]+1ll*(n-cnt)*a.a[1][1])%MOD;
if(h[1]) ans=(1ll*n*(x+y)-1ll*g[1]*x)%MOD;//若以 1 为根必胜,我要求不能改变根的状态
else ans=1ll*g[1]*x%MOD;//否则要求必须改变
return printf("%d",ans),0;
}
P4657 [CEOI2017] Chase#
题目大意#
见口胡。
Solve#
同一条路径正着走,倒着走的贡献是不同的。
考虑枚举每个点作为起点,把起点当做根,那么在一个点放磁铁的贡献 即为所有儿子权值和。
考虑 表示以 为根的子树内选了多少个点放磁铁,转移如下。
复杂度是 的。
那么我们考虑实际上一个点的更新是在原树上从父亲或者儿子转移来。
直接设一个 dp 状态为: 表示从 走向 的子树内,选了 个, 选或不选。
表示从 的子树走向 ,选了 个, 选或不选。
那么有转移式:
关于初值 , 是不合法情况,负无穷即可; 表示以 为起点,所以贡献是 。
更新答案的话,我们在 dp 过程中一起更新了,一条路径可以由一条从下往上走的路径拼一条从上往下走的路径,还可以由一条从上往下走的路径拼一条从下往上走的路径。
要求 。最后答案即为:
Code#
HERE。
P2664 树上游戏#
题目大意#
给定一颗树,每个节点一个颜色,对于树上的每条路径,定义路径上的颜色数为 ,定义 ,求所有的 。
Solve#
算法一:点分治#
直接大力点分治。
考虑点分治的过程中将每种颜色的贡献拆开:
- 如果从分治中心到当前节点中没有出现某种颜色,那么它产生贡献的路径一定跨越了其他子树中的这种颜色。所以说我们维护这种颜色在别的子树中覆盖的子树大小即可。
- 如果出现了,那么对于先前遍历过的每颗子树都能产生整个子树大小的贡献,加上就行了。
但是比较难维护,细节有点多,在这里不多赘述。
代码:提交记录
时间复杂度:。
当然,因为是树形 dp 专题,所以我们还有线性做法。
算法二:树形 dp#
还是将贡献拆开来算。
考虑对于一个点,对于一种确定的颜色,不能对答案造成贡献的点一定构成一个连通块,如图:
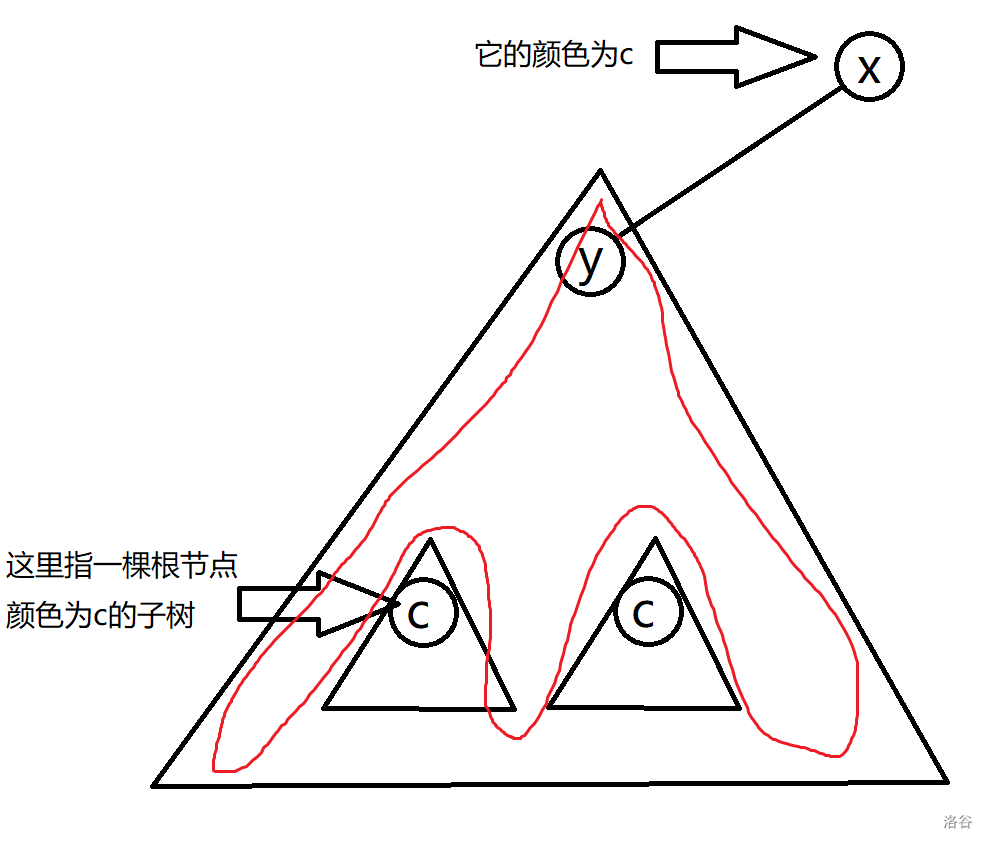
我们将从出发的路径对于颜色 不能造成贡献的点数记为 ,显然我们不能直接统计(废话),然后我们不难发现对于图中红色部分的这些点他们的 都是中间的连通块大小,所以说我们不妨直接做树上差分,最后对于每个点,其答案就是,其中 为种类数。
时间复杂度:。
P4099 [HEOI2013] SAO#
题目大意#
给定一棵 个节点的树,树上的边是有向的,问这棵树有多少种不同的拓扑序。
Solve#
考虑如果边的指向都是从父亲到儿子,怎么做。
考虑如下 DP:设 表示 的子树有多少种拓扑序。如何转移?
利用 dfs 的过程,现在已经遍历了 个儿子,前 个儿子的 之和为 ,第 个儿子为 ,则有:
即要求这 个点在拓扑序中都在 之后, 之后现在总共有 个位置,从中任意选出 个位置填进去。'
那么现在有从儿子连向父亲的边,如何处理?
考虑一条边 (u,v) 的指向,它的限制实质上是要求拓扑序中 在 之前或之后,并且只对 和 的相对位置有要求。所以我们考虑 DP 状态再添一维。
设 表示仅考虑 的子树,节点 位于拓扑序中的 位置的方案数。分情况讨论转移。
- 如果 是从 指向 ,要求 在 之前。考虑钦定从 的子树中选出来 个放在 前面,那么需要 在其子树中的位置 。所以我们维护 的前缀和即可。转移系数为在 左边新加入 个位置,然后选出 个位置的方案数,再乘上在 右边新加入 个位置,然后选出 个位置的方案数,即 , 的意义和上面一样。
- 否则,要求 在 之后。类似的,钦定从 的子树中选出来 个放在 前面,需要 在其自述中的位置 。转移系数一样的,维护后缀和即可。
Code#
void dfs(int u,int fa)
{
siz[u]=1;f[u][1]=1;
for(int v=1;v<=n;v=-~v)
if(e[u][v]&&v!=fa)
{
dfs(v,u);
for(int i=1;i<=siz[u];i=-~i) g[u][i]=f[u][i],f[u][i]=0;
if(e[u][v]<0)
for(int i=1;i<=siz[u];i=-~i)
for(int j=1;j<=siz[v];j=-~j)
(f[u][i+j]+=1ll*pre[v][j]*g[u][i]%MOD*c[i+j-1][j]%MOD*c[siz[u]-i+siz[v]-j][siz[v]-j]%MOD)%=MOD;
else
for(int i=1;i<=siz[u];i=-~i)
for(int j=0;j<siz[v];j=-~j)
(f[u][i+j]+=1ll*suf[v][j+1]*g[u][i]%MOD*c[i-1+j][j]%MOD*c[siz[u]-i+siz[v]-j][siz[v]-j]%MOD)%=MOD;
siz[u]+=siz[v];
}
for(int i=1;i<=siz[u];i=-~i)
pre[u][i]=(pre[u][i-1]+f[u][i])%MOD;
for(int i=siz[u];i;i=~-i)
suf[u][i]=(suf[u][i+1]+f[u][i])%MOD;
}
inline void solve()
{
n=read();
for(int i=1;i<=n;i=-~i)
for(int j=1;j<=n;j=-~j)
e[i][j]=f[i][j]=g[i][j]=pre[i][j]=suf[i][j]=0;
for(int i=1,u,v,c;i<n;i=-~i)
{
u=read()+1;c=getchar();v=read()+1;
if(c=='<') e[u][v]=1,e[v][u]=-1;
else e[u][v]=-1,e[v][u]=1;
}
dfs(1,0);ans=0;
for(int i=1;i<=n;i=-~i) (ans+=f[1][i])%=MOD;
printf("%d\n",ans);
}
P3748 [六省联考 2017] 摧毁“树状图”#
题目大意#
选择树上两条边不交路径,使得删去后剩下联通块数目最多,当然,部分分给的很多。
Solve#
我们想一个树形dp。
- : 切除一条端点在 且另一端点在子数内的链的答案,这条链就像这样:
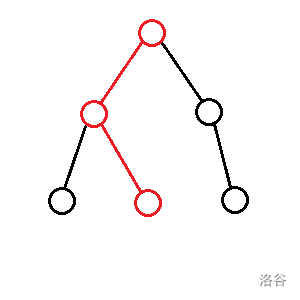
- :切除一条两个端点在 子树内且链不经过 的链的答案:
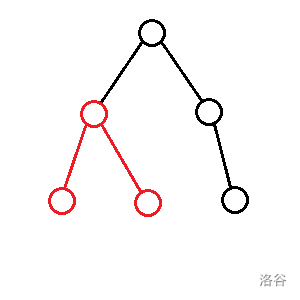
- : 切除一条两个端点在 子树内且经过 的链的答案:
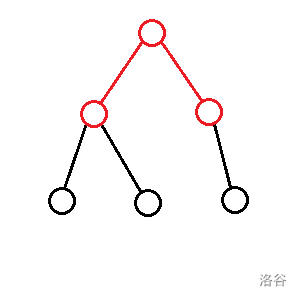
- :切除一条端点在 且另一端点在子数内的链与一条两个端点在 子树内且经过 的链的答案:
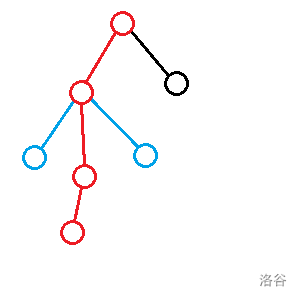
答案即可用这些更新。
我们想答案会长什么样:
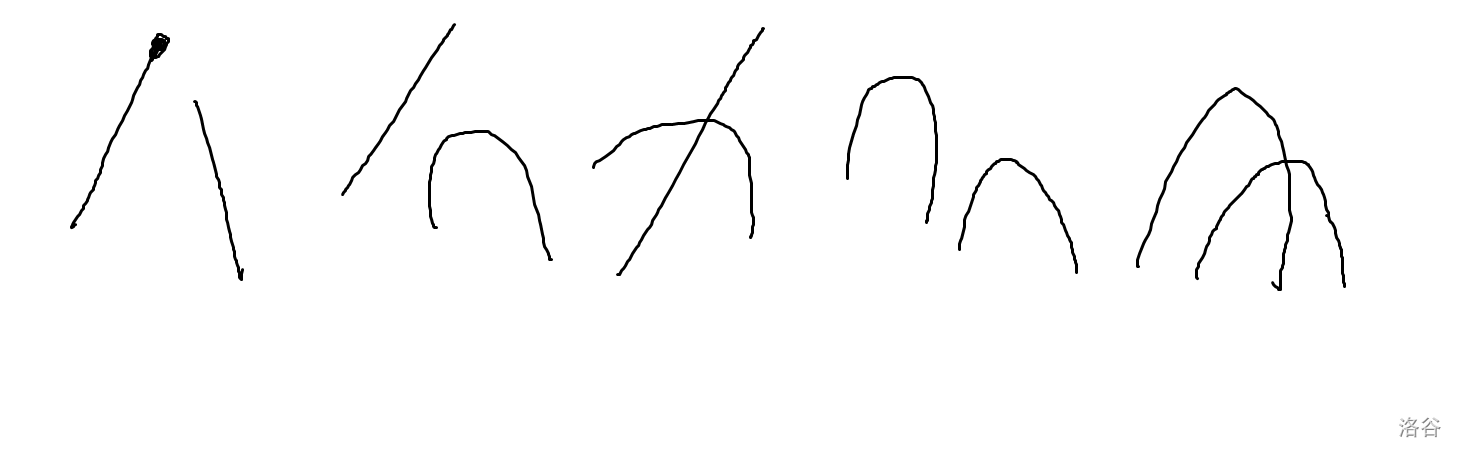
那么更新有6种方式。
- (因为如果 是 1 那么上方没有其他连通块要减掉 1,之后同理):
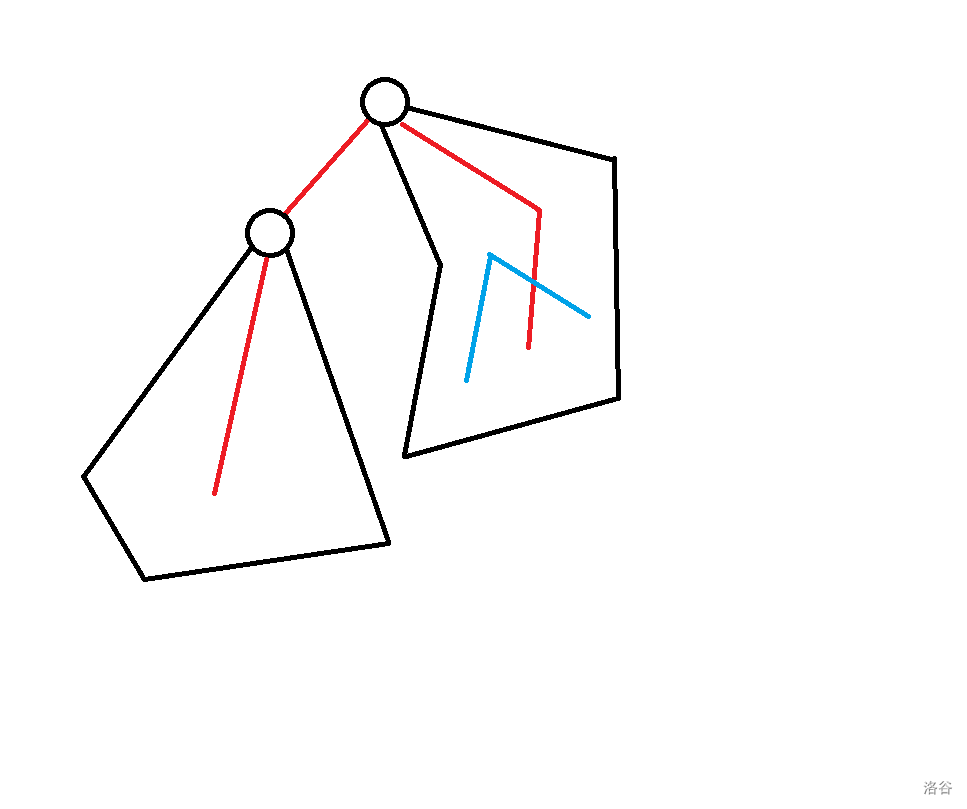
- :
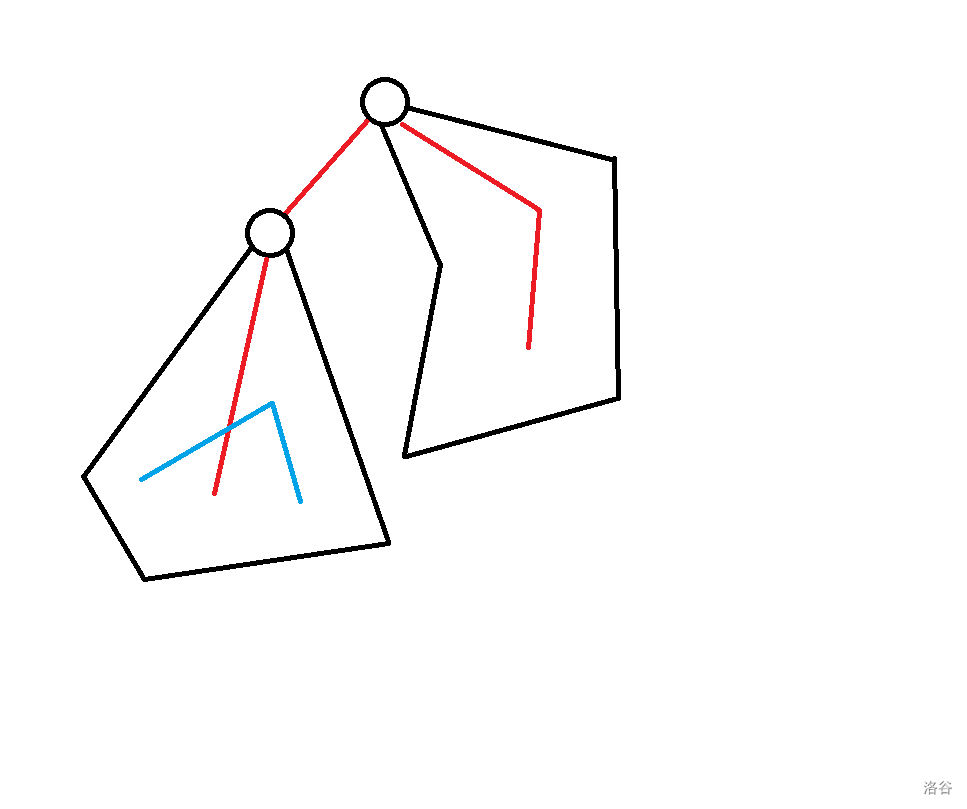
- (因为无论 上方有没有节点都不影响答案所以不需要判 为 ):
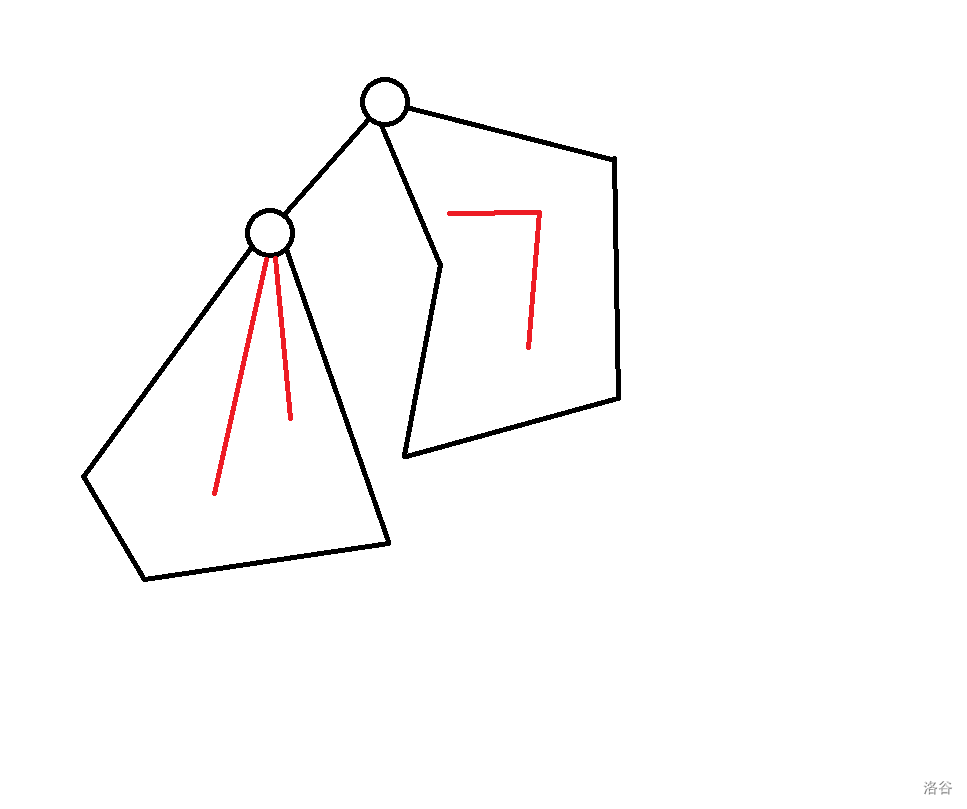
- (上方没切到的地方连到一起了多算了一个要减一):
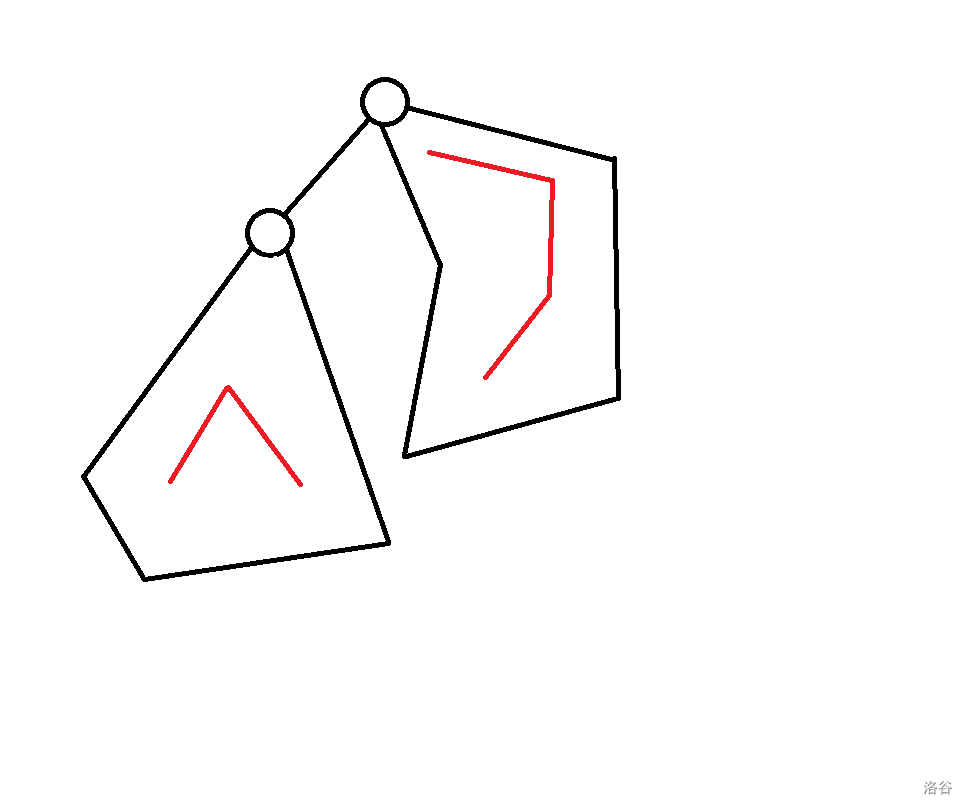
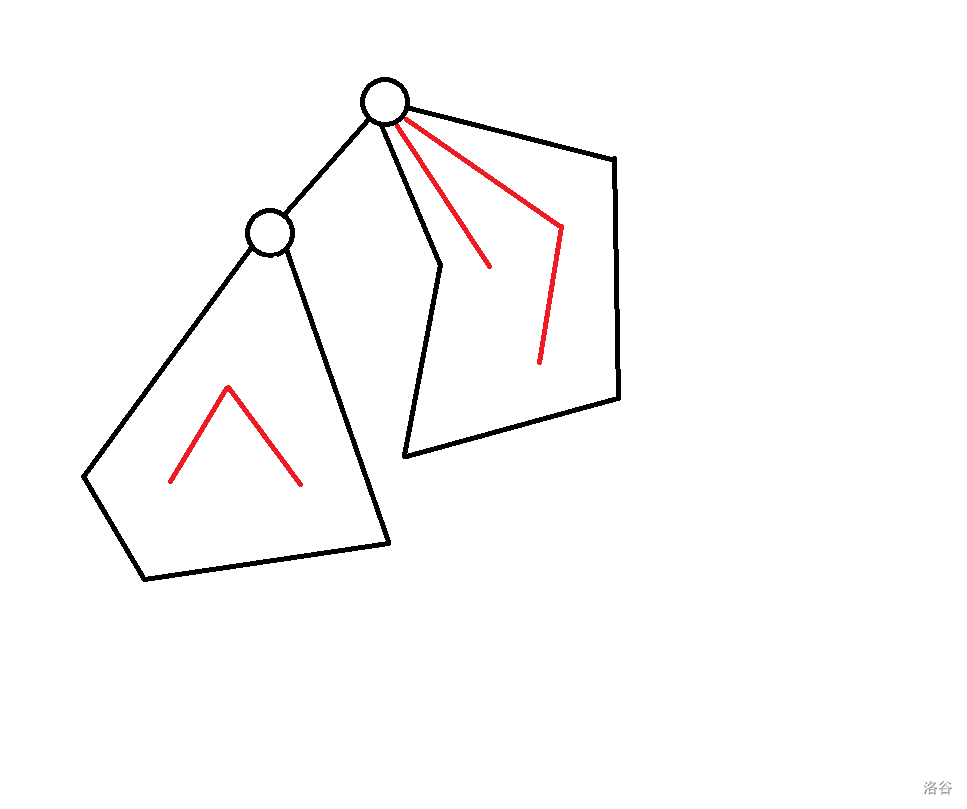
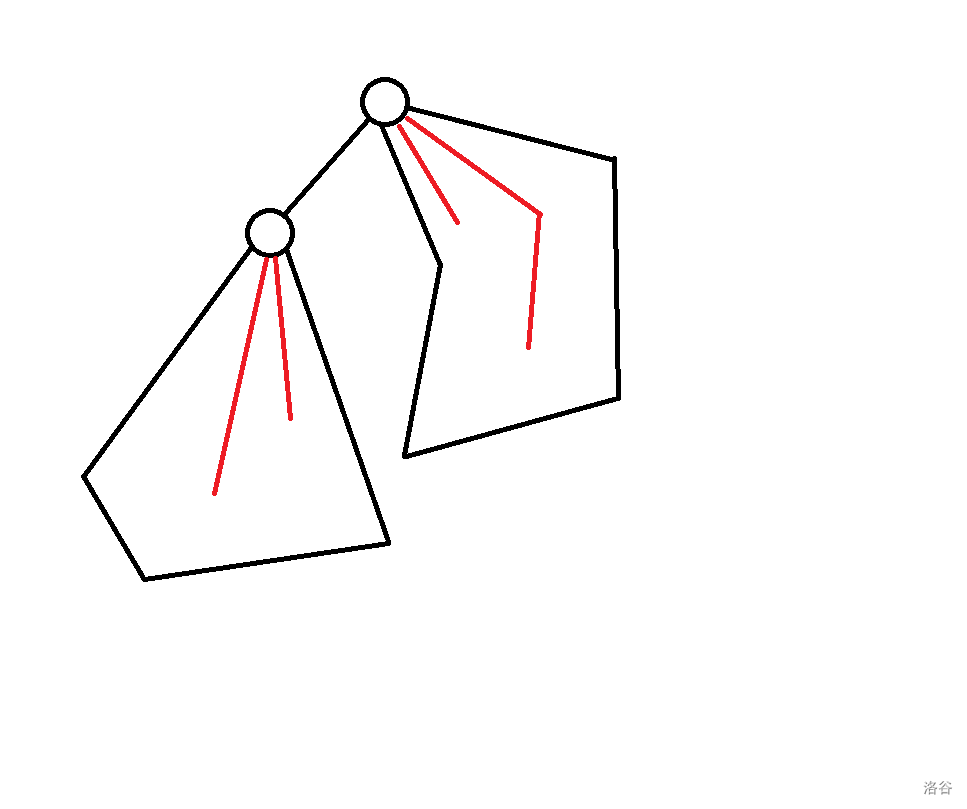
- 有一种方案可以推得 ,即直接在 的基础上删掉节点 ,(其中 的意思是 p 的儿子数):
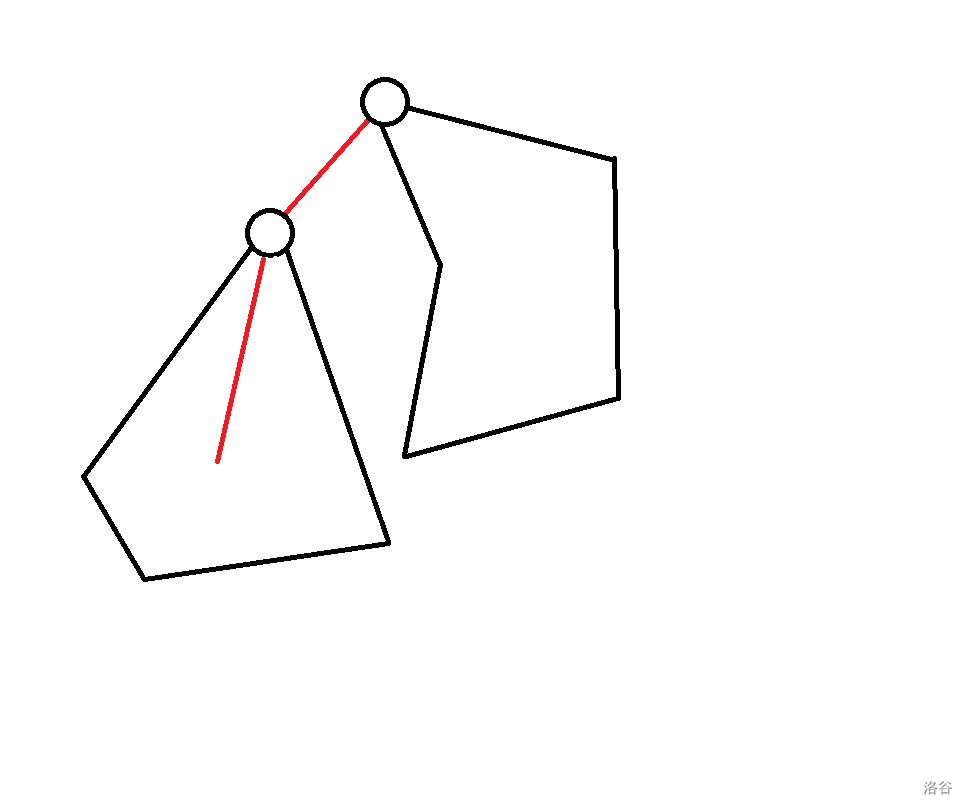
有两种方案可以推得 :
- 直接继承
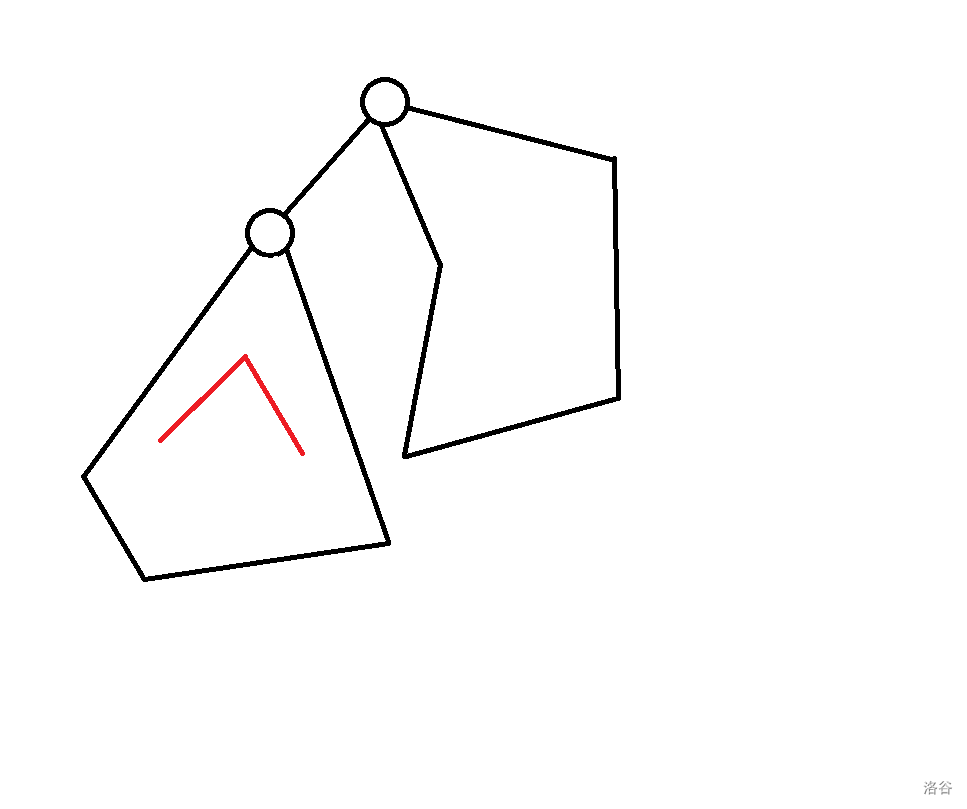
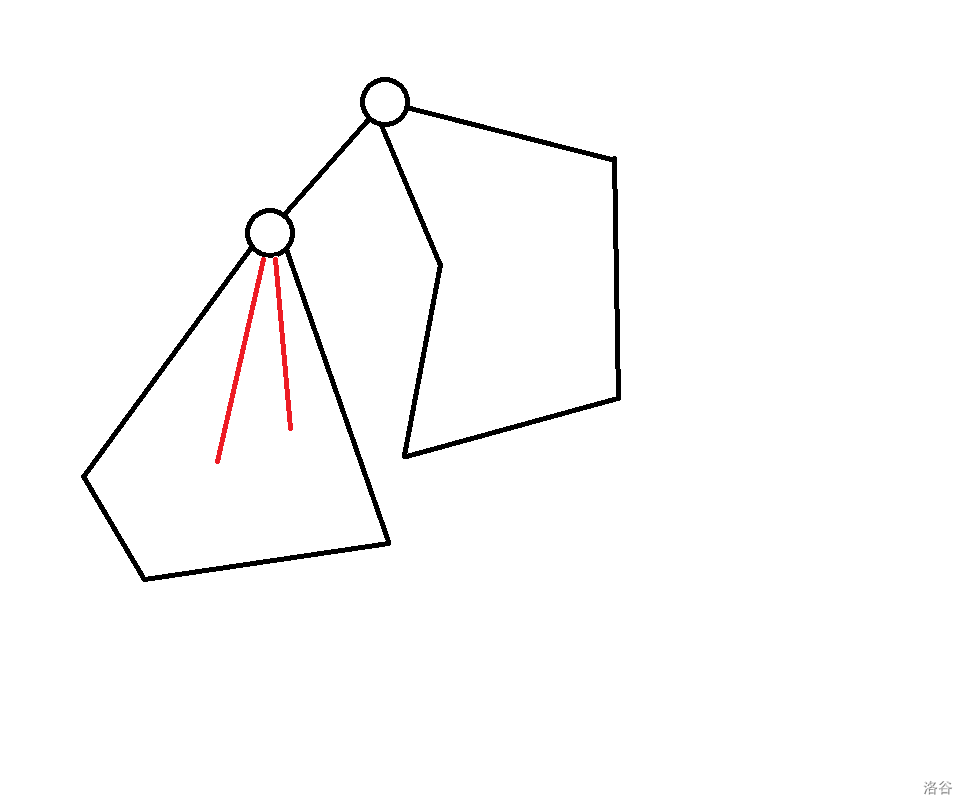
有一种方案可以推得 ,即 :
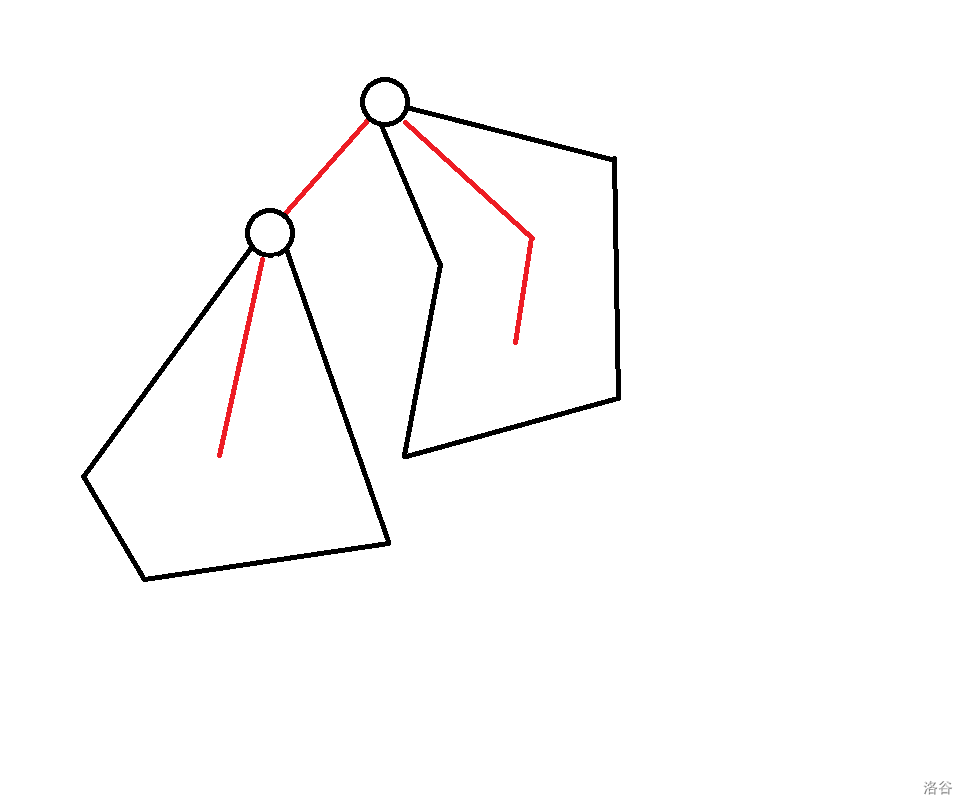
有五种方案可以推得 :
- :
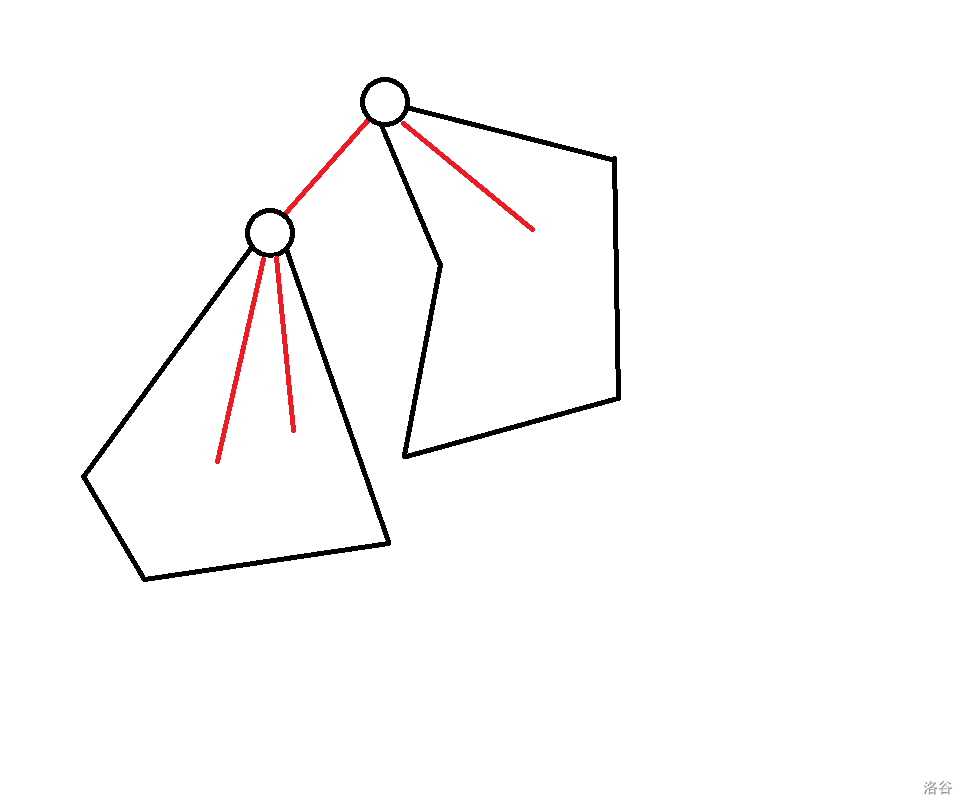
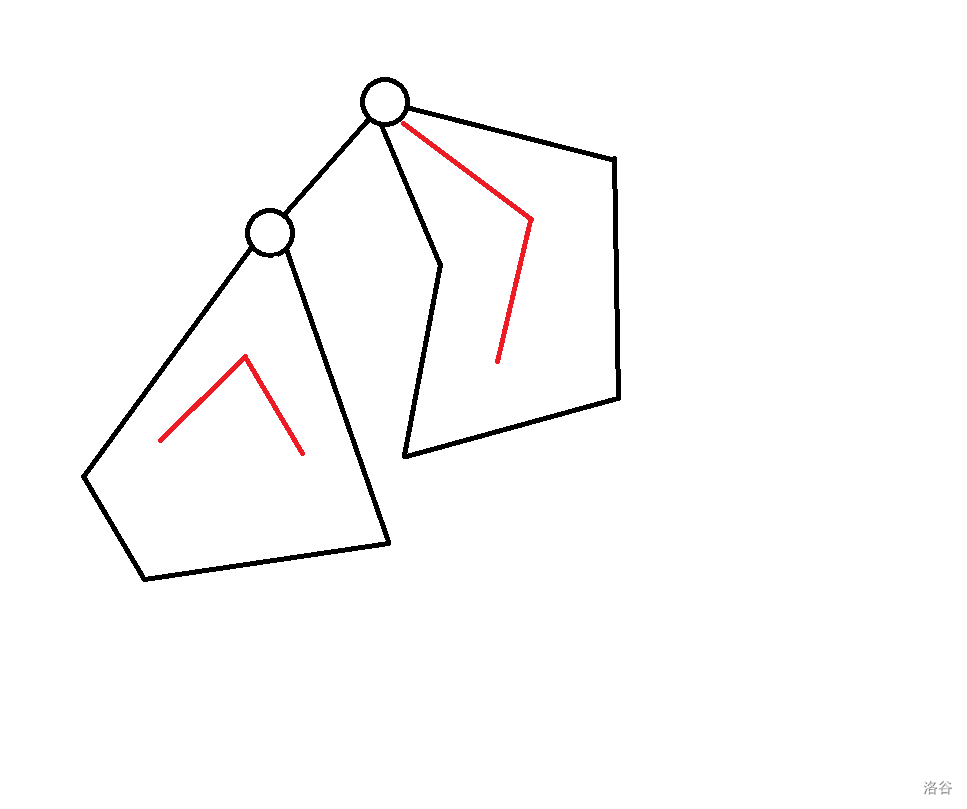
- :
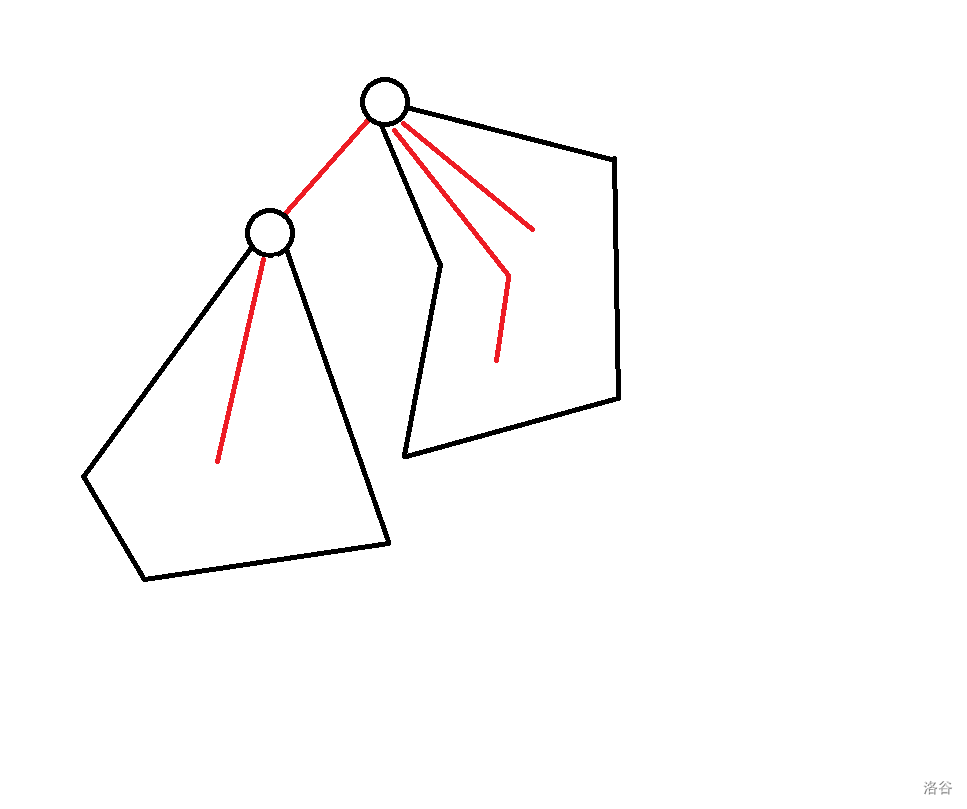
- :
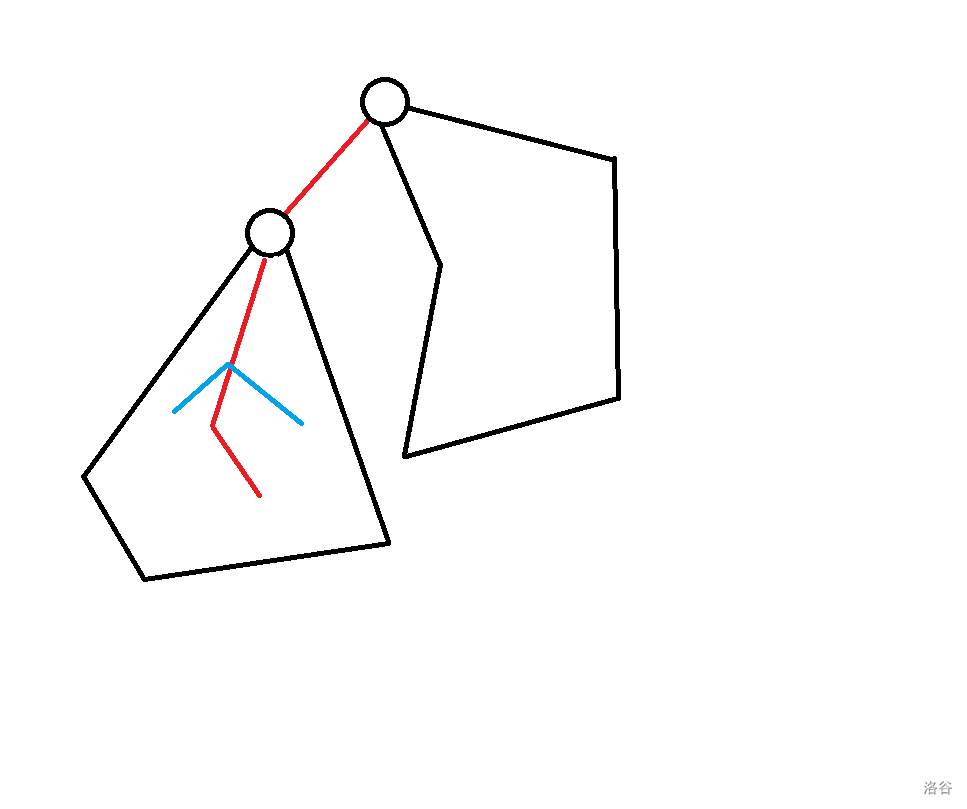
- :( 的意思是之前讨论的儿子 q 中最大的 和 )
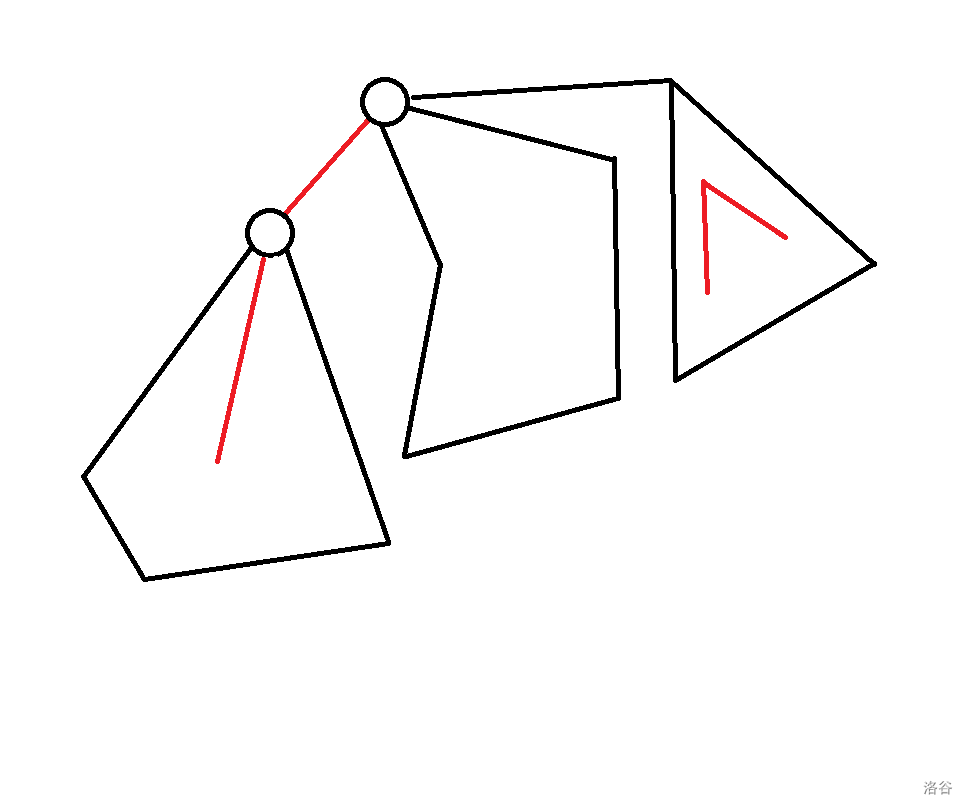
初始化的问题: 和 , 设为 即只切掉节点 p; 设为 1,即不切。
Code#
int f[N][4];//0表示从x向下延伸,1表示子树内选一条路径,2表示过x选一条路,3表示从x向下选一条路径,在子树中加一条路径
void dfs(int x,int fa)
{
f[x][0]=f[x][3]=f[x][2]=deg[x];//切x
f[x][1]=1;//不切
int mx=0;
for(auto y:v[x])
if(y!=fa)
{
dfs(y,x);
ans=max({ans,f[x][3]+f[y][0]-(x==1),f[y][3]+f[x][0]-(x==1),f[x][1]+f[y][2],f[x][1]+f[y][1]-1,f[x][2]+f[y][1]-(x==1),f[x][2]+f[y][2]-(x==1)});
f[x][1]=max({f[x][1],f[y][1],f[y][2]+1});
f[x][3]=max({f[x][3],f[y][3]+deg[x]-1,f[y][0]+deg[x]+mx-2,f[x][2]+f[y][0]-1,f[x][0]+f[y][2]-1,f[x][0]+f[y][1]-1});
f[x][2]=max(f[x][2],f[x][0]+f[y][0]-1);
f[x][0]=max({f[x][0],f[y][0]+deg[x]-1});
mx=max({mx,f[y][1],f[y][2]});
}
}
signed main()
{
T=read(),op=read();
while(T--)
{
ans=0;
n=read();
for(int i=1;i<=n;i++) v[i].clear(),deg[i]=0;
int x,y;
if(op==1) read(),read();
if(op==2) read(),read(),read(),read();
for(int i=2;i<=n;i++)
{
x=read(),y=read();
v[x].push_back(y);
v[y].push_back(x);
deg[x]++,deg[y]++;
deg[i]--;
}
dfs(1,0);
cout<<ans<<endl;
}
return 0;
}
【UNR #5】提问系统#
题目大意#
见题意描述: 【UNR #5】提问系统 。
Solve#
首先暴力有20分。
然后,考虑我们可以把所有的操作建模成一棵树。从根节点( 节点)出发,对于一个 push 操作,我们将它视为从当前所在节点新建一个儿子节点,并且移动到这个儿子上;对于一个 pop 操作,我们将它视为到达当前节点的父亲节点。那么问题实际转化为:用两种颜色对这棵树的节点进行染色,要求从根出发到任意一个叶子节点的路径上 的个数均不超过限制,对于所有合法的方案,如果其 个数为 ,那么对答案做出的贡献为 。那么就可以考虑树形 dp 做这个东西了。
暴力1#
我们设出状态为 ,表示在以 为根的子树中, 的最大出现次数为 ,并且 的总个数为 的总方案数。然后答案就是:
时间复杂度: / 。
暴力2#
在第一个暴力的基础上,发现如果同时枚举 的出现次数造成了时间复杂度的增多,根本原因在于无法确定子树内每一条链的形态,所以考虑转换状态的设计。
将状态设为 ,表示从 到根的这条链中(不包含 ) 的个数有 个,以 为根的子树中存在 个 的方案数,然后从叶子开始 dp 每次到父亲处合并即可。
最后的答案就是:
时间复杂度: / ,具体看实现。
代码:提交记录。
正解#
发现对于现在的状态,第一维枚举节点,是无法继续优化的;第二维已经优化过一次,并且必须保留这一维对方案的统计进行约束,所以也无法继续优化;第三维统计子树中某种颜色的个数,是为了最后统计答案,考虑从这一维入手继续优化 dp。
发现对于答案,有转化:
这个东西的组合意义就是对于一颗已经染过色的合法的树,有序地选一个 点,两个 点(可重复)的方案数。所以说我们没有必要存下来子树内所有的点数,只需要记录 ,前两维意义不变,后面表示已经选了 个 ,已经选了 个 的方案数,这样在转移时就避免了枚举子树内点数的复杂度。
最终答案就是:
时间复杂度:
代码:提交记录。
ARC179D Portable Gate#
题目大意#
你在一棵 个节点的树上并且有一个门。选定任意节点作为起点,然后每次执行以下操作之一:
- 移动到当前节点的相邻节点,耗费代价 1;
- 移动到门所在节点;
- 将门移动到当前节点。
求至少消耗多少代价能遍历树上的所有节点。
Solve#
将选定的起点视为根,考虑树形 DP。
设 表示将 的子树内遍历完回到 所需的最小代价,那么对于一个儿子 ,转移分两种情况:
- 门放在 上,徒步走完 的子树。
- 门放在 上,可以使用门走完 的子树。
考虑徒步走完 的子树代价是多少,由于门放在 上,最后可以传送回来,显然我应该走到 的子树内的最深的那个叶子后传送回来。所以记 子树内最深的叶子到 的距离是 。记徒步走完 的子树的代价为 ,则 。
所以有转移:
代表只走 1 步到 ,走完 的子树后用门传送回来。 表示走一步到 ,带门走完 子树后再走 1 步回来。
但是,题目并没有要求最后必须回到起点,所以 现在的意义是不够的,我们还应讨论遍历完 的子树后是否回到节点 。由此我们改变一下状态。
记 表示遍历完 的子树,是 / 否回到节点 的最小代价。 还是沿用上面的状态转移,对于 ,我考虑去枚举最后落在 的哪个儿子的子树里,这个儿子记为 ,那么我要求遍历除了 的其他所有儿子的子树后,都要回到节点 ,只有 不需要。那么只需把 的贡献从 中刨去,再加上不要求遍历 的子树后回到 的贡献。
至于怎么算这个贡献,还是上面的分情况讨论。若门在 上,则代价为 ,否则若带门进 的子树,代价为 。
所以记 为 对 的贡献,那么有:
这样我们就处理完了根固定时的答案。接下来考虑换根。
感觉线性换根非常困难,我不会。但由于数据范围是 ,所以我们可以考虑用比较苟脑的带 的换根方式。
考虑把 的所有儿子 的 和 分别放进 set 里,换根时只需要用 set 的 erase 函数就可以把 的贡献从 里刨去,刨去后容易算出以 为根时的 ,用这些信息更新 的相应值和 的两个 set 即可。具体看代码吧。
Code#
std::set<std::pair<int,int>>s[N],q[N];
void F(int u,int fa)
{
for(int v:e[u])
if(v!=fa)
{
F(v,u);
f[u][1]+=min(f[v][1]+2,g[v]+1);
q[u].insert({t[v],v});
siz[u]+=siz[v];s[u].insert({h[v],v});
}
f[u][0]=f[u][1];
if(!s[u].empty())//谨防RE
{
f[u][0]=min(f[u][0],f[u][1]+q[u].begin()->first);
h[u]=s[u].rbegin()->first+1;
}
g[u]=(siz[u]++<<1)-h[u];
t[u]=-min(f[u][1]+2,g[u]+1)+min(f[u][0]+1,g[u]+1);
}
void G(int u,int fa)
{
int _f[2],_h,_g,_t;//把某个儿子刨去后的相应值
for(int v:e[u])
if(v!=fa)
{
s[u].erase({h[v],v});q[u].erase({t[v],v});
_h=s[u].empty()?0:s[u].rbegin()->first+1;
_g=(n-siz[v]-1<<1)-_h;
_f[1]=f[u][1]-min(f[v][1]+2,g[v]+1);
_f[0]=_f[1];
if(!q[u].empty())//谨防RE
_f[0]=min(_f[0],_f[1]+q[u].begin()->first);
_t=-min(_f[1]+2,_g+1)+min(_f[0]+1,_g+1);
q[v].insert({_t,u});s[v].insert({_h,u});//更新儿子的 set
f[v][1]+=min(_f[1]+2,_g+1);
f[v][0]=min(f[v][1],f[v][1]+q[v].begin()->first);
s[u].insert({h[v],v});q[u].insert({t[v],v});
G(v,u);
}
}
signed main()
{
n=read();
for(int i=1,u,v;i<n;i=-~i)
u=read(),v=read(),
e[u].push_back(v),e[v].push_back(u);
F(1,0);G(1,0);
for(int i=1;i<=n;i=-~i) ans=min(ans,min(f[i][0],f[i][1]));
return printf("%d",ans),0;
}
P2081 [NOI2012] 迷失游乐园#
题目大意#
你一颗树或者基环树,要求随机选择一条路径的期望长度,同时要求路径终点所连的所有点都已被选择。
Solve#
Sub 1-5#
我们考虑树怎么做,我们很容易想到一个 的暴力 dp,即枚举一个点,以他为根,dp[x] 表示x子树内贡献,则转移式如下:
实际实现时,要考虑到分母为 0 的情况,要不然会获得 nan 的好输出。
此部分代码如下:
void dfs(int x,int fa)
{
for(int i=0;i<v[x].size();i++)
{
int y=v[x][i].first;
double val=v[x][i].second;
if(y==fa)continue;
dfs(y,x);
dp[x]+=(dp[y]+val);
}
if(x==1) dp[x]*=(1.0/(double)(v[x].size()));
else {
if(v[x].size()!=1) dp[x]*=(1.0/(double)(v[x].size()-1));
}
}
显然,这个枚举根的过程可以用换根来优化掉,我们只需要将 dp[x] 减去 y 作为其子树的贡献,在用 dp[x] 去更新 dp[y] 即可,复杂度为 代码如下:
void Dp(int x,int fa)
{
double tmpx,tmpy;
for(auto [y,val]:v[x])
{
if(y==fa||vis[y])continue;
tmpx=dp[x],tmpy=dp[y];
dp[x]-=(dp[y]+val)/deg[x];
if(deg[x]>1)dp[x]=dp[x]*deg[x]/(deg[x]-1);
else dp[x]=0;
dp[y]=dp[y]*(deg[y]-1)/deg[y];
dp[y]+=(dp[x]+val)/deg[y];
ans+=1.0/n*dp[y];
Dp(y,x);
dp[x]=tmpx,dp[y]=tmpy;
}
}
至此,就可以获得 50 分的好成绩了。
Sub 6-10#
树我们已经会了,那我们考虑基环树怎么做,同时题目要求也说明了 环的大小 小于等于 20,我们可以从这里入手,我们考虑将图变成这样。
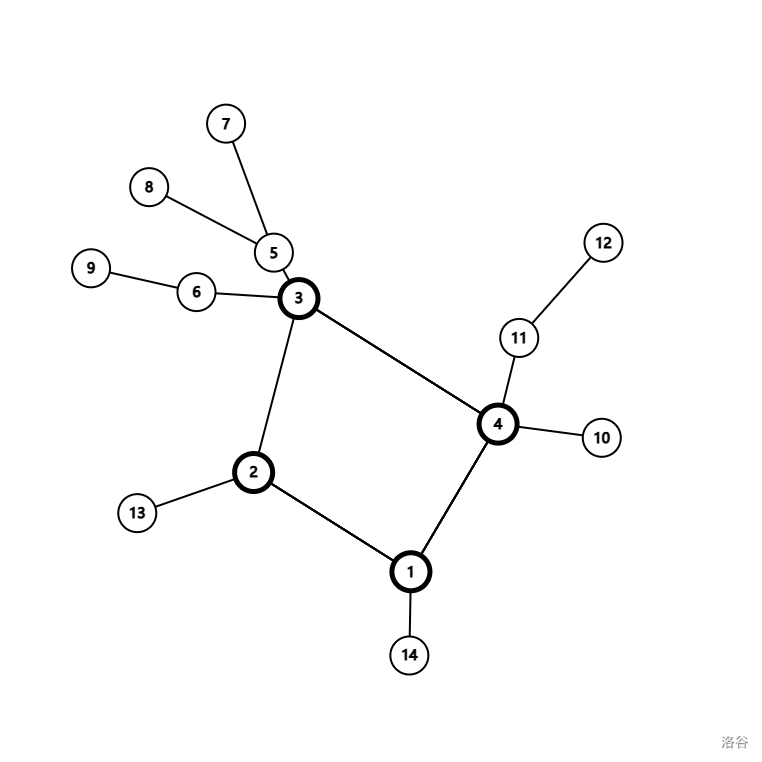
我们发现图变成了,中间一个环,环上每个点作为根,连了一棵树出来,这样的话, 我们只需要求出环上每个点作为全局根的 dp 值就可以向他的子树内换根了。
现在我们考虑如何求出环上一点的全局 dp 值,从环上点出发的一条合法路径一定形似这个点走到环上另一点的子树内,
或者仅仅只有一个环的时候,就是走完一整个环结束。
那环的大小又这么小,我们考虑枚举起点,并顺时针枚举终点,逆时针同理,我们只需再做一遍即可,用终点的 dp 值更新起点的 dp 值,再从起点向子树内换根就可以。
具体实现的话就是:
我们维护一个概率 ,和距离 , 的更新就是到每个点我们更新 为 因为来时路已经不能走了,所以要减 1,当然结算每个点的贡献时要考虑一个额外的概率,就是我们走进这个点的子树内的概率,即为 ,还有一个细节是,在走到最后一个环上这个点的时候,我们就不用考虑上面说的这个额外概率了,因为此时只能走进这个点的子树内了。
代码实现。
CF1981F Turtle and Paths on a Tree#
题目大意#
给你一棵 二叉树,点有点权,你需要把这棵树的边集划分成若干条路径,边不能有交,但点可以有交,每条路径的代价定义为经过的点的点权的 ,这里 指的是最小的未出现过的 正整数,一组划分方案的代价定义为所有路径的代价之和。求划分方案的最小代价?
Solve#
树上划分路径,朴素的想法是直接设 表示从 号点往子树里延伸了一条链,该子树划分的最小代价。
但路径的代价是点权 ,这玩意很难直接维护,有一个做法是加一维状态 表示这条链从 到 ,由于涉及两个儿子中路径的合并,复杂度可能是 ,大概过不了。
更好的做法是分析一下性质,题目中需要求的是 之和最小值, 的定义是 “最小的未出现过的正整数”。
我们可以有这么一个想法:对于一条路径,枚举 ,钦定 没有在点权中出现过,然后直接认为 就是路径 。
这样做首先一定不会比真正的 还小,同时随着 的枚举,真正的 必然能够取到。
那么我们的做法,设 表示 号点往子树里延伸的一条链,钦定链上 没有出现过,子树里划分的最小代价。
转移应该比较简单。
发现这样做看上去还是 的,但我们 (题解) 有一个结论:最优方案中 的取值不会超过 。

本题还有启发式 / 线段树合并做法。
Code#
void dfs( int x )
{
if( ls[x] ) dfs(ls[x]) ;
if( rs[x] ) dfs(rs[x]) ;
if( !ls[x] ) {
for(int j = 1 ; j <= P ; j ++ ) {
if( j!=a[x] ) f[x][j] = 0 ;
else f[x][j] = inf ;
}
}
else {
if( !rs[x] ) {
int Min = inf ;
for(int j = 1 ; j <= P ; j ++ ) {
if( j!=a[x] ) {
Min = min( Min , f[ls[x]][j]+j ) ;
}
}
if( x==1 ) ans = min( ans , Min ) ;
for(int j = 1 ; j <= P ; j ++ ) {
if( j!=a[x] ) f[x][j] = min(Min,f[ls[x]][j]) ;
else f[x][j] = inf ;
}
}
else {
int Min1 = inf , Min2 = inf , Min3 = inf ;
for(int j = 1 ; j <= P ; j ++ ) {
if( j!=a[x] ) Min1 = min( Min1 , f[ls[x]][j]+j ) , Min2 = min( Min2 , f[rs[x]][j]+j ) , Min3 = min( Min3 , f[ls[x]][j]+f[rs[x]][j]+j );// Merge
}
if( x==1 ) ans = min({ ans , Min1+Min2 , Min3}) ;
for(int j = 1 ; j <= P ; j ++ ) {
if( j!=a[x] ) f[x][j] = min({ Min1+Min2 , Min3 , Min2+f[ls[x]][j] , Min1+f[rs[x]][j]}) ;
else f[x][j] = inf ;
}
}
}
}
void solve()
{
scanf("%d" , &n ) ;
for(int i = 1 ; i <= n ; i ++ ) {
scanf("%d" , &a[i] ) ;
a[i] = min(a[i],n+1) ;
ls[i] = rs[i] = 0 ;
}
int x ;
for(int i = 2 ; i <= n ; i ++ ) {
scanf("%d" , &x ) ;
if( !ls[x] ) ls[x] = i ;
else rs[x] = i ;
}
ans = inf ;
P = min(M,n+1) ;
dfs( 1 ) ;
printf("%d\n" , ans ) ;
}



 好困难啊,树d
好困难啊,树d


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· 单线程的Redis速度为什么快?
· 展开说说关于C#中ORM框架的用法!
· Pantheons:用 TypeScript 打造主流大模型对话的一站式集成库
· SQL Server 2025 AI相关能力初探