STM32使用FFT变换计算THD（20年四川省电子设计大赛E题软件部分）

注： 本篇内容意在使不理解FFT变换的读者也可以通过使用FFT来计算总谐波失真

FFT变换

根据总谐波失真的定义：

\[THD = \frac{\sqrt{\sum_{n=0}^{\infty}{G_{n}^{2}}}}{G_0} (G_0为基波，G_n 为高次谐波) \]

可知，要计算THD需要知道基波分量和各个谐波分量的大小。

​ FFT也叫快速傅里叶变换，是离散时间傅里叶变换的一种实现手段，变换的本质还是离散时间傅里叶变换（DTFT）。傅里叶变换可以将信号从时域展开到频域，通过FFT变换即可实现对信号基波和谐波分量的计算。

STM32F4进行FFT

​ 如果不熟悉傅里叶变换，也无关紧要，你只要知道FFT变换可以得到信号在各个频率上的分量，以STM32F407VGx为例，我们可以使用ST提供的DSP库快速实现FFT变换。

​ 这里使用cube MX生成一个简单的工程作为模板，首先加入一些使用DSP库所需要的宏定义：

,ARM_MATH_CM4,__CC_ARM,ARM_MATH_MATRIX_CHECK,ARM_MATH_ROUNDING

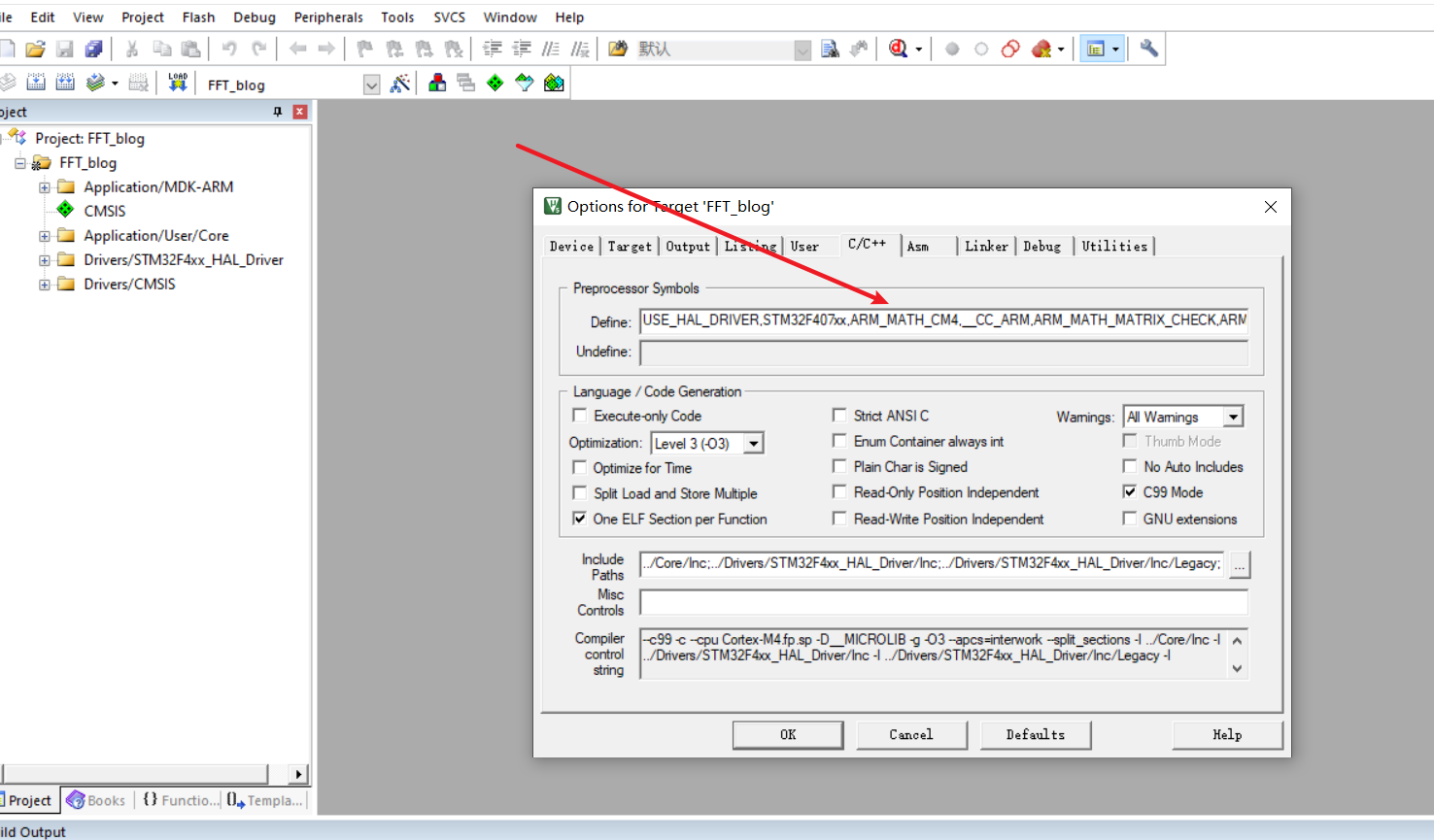
然后，进入CubeMX的安装目录，找到DSP库下的几个文件

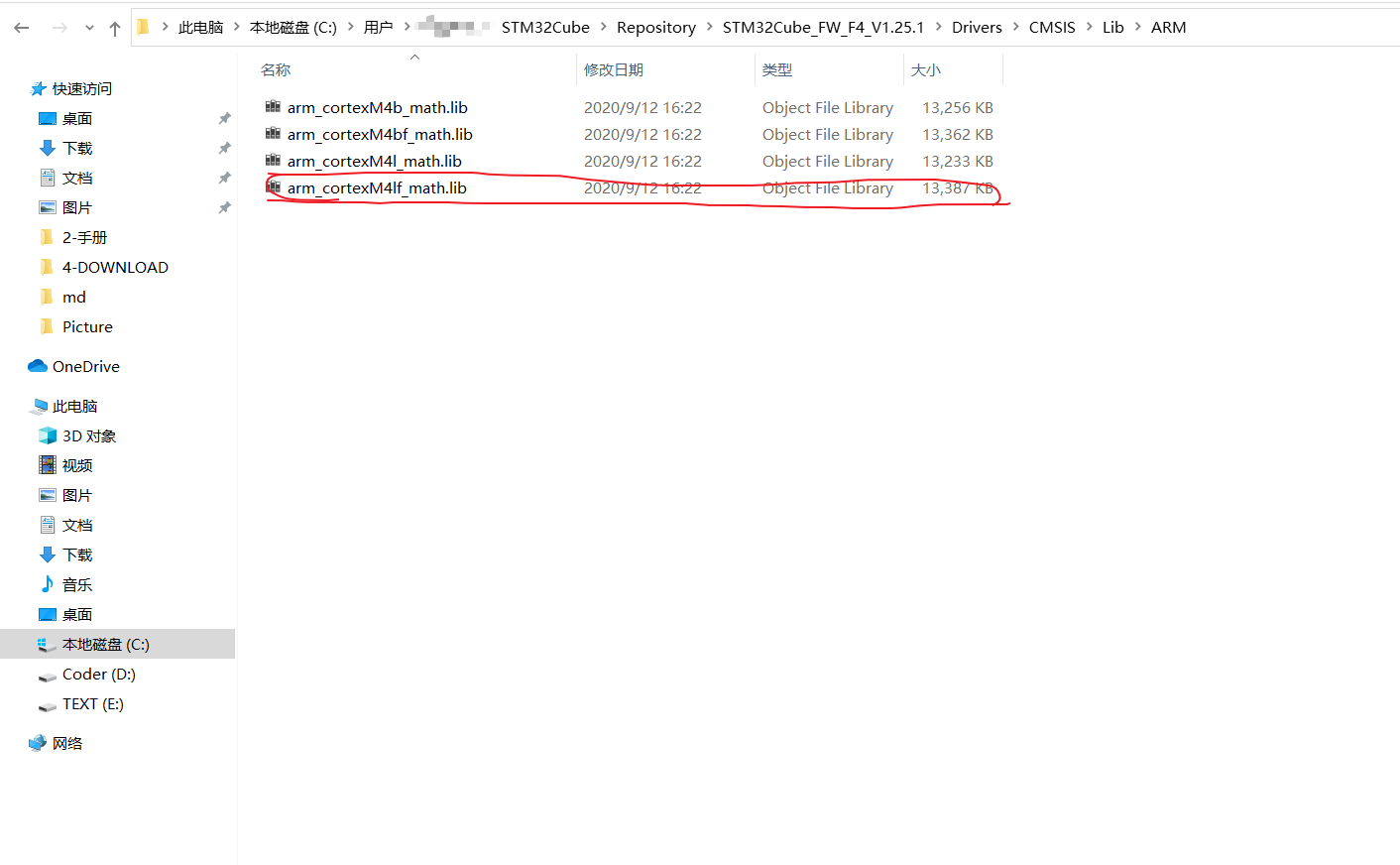
首先lib文件：

​ arm_cortexM4lf_math.lib

cortexM4 是指 arm的cortexM4内核，后面的l 是指芯片使用小端存放，f是浮点运算，STM32F4 默认是小端存放所以使用这个库文件

位置C:\Users\Username\STM32Cube\Repository\STM32Cube_FW_F4_V1.25.1\Drivers\CMSIS\Lib\ARM 下、

然后是头文件

位置在

C:\Users\Username\STM32Cube\Repository\STM32Cube_FW_F4_V1.25.1\Drivers\CMSIS\DSP\Include

将这三个文件加入工程中

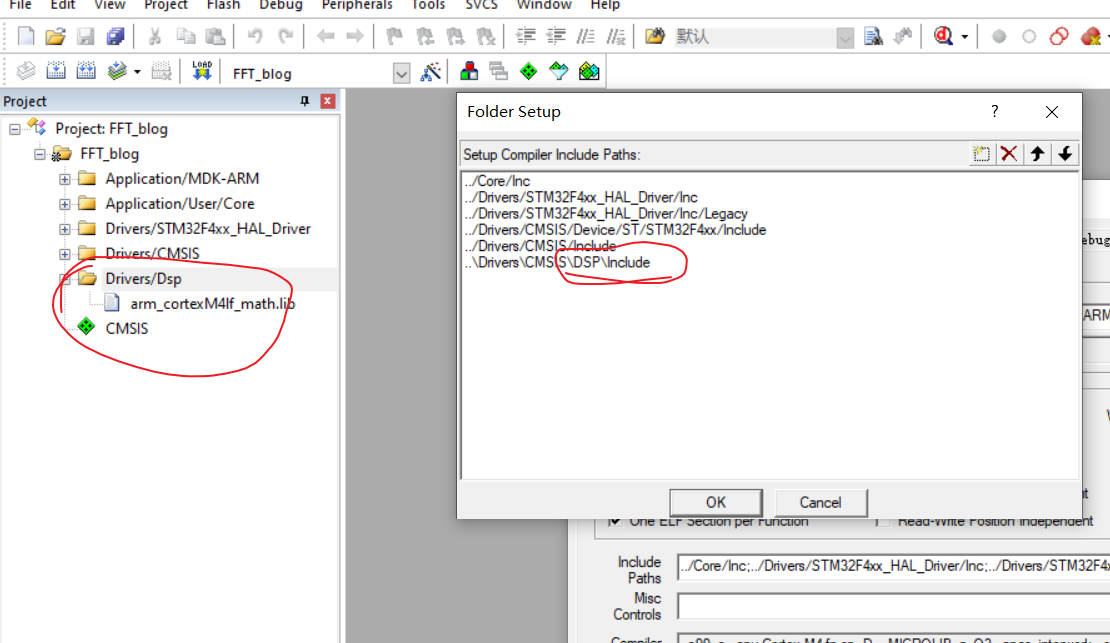
注意：

如果是和我一样通过CubeMX生成的工程，且在code Generator中选择了Copy all library into the floder 如图

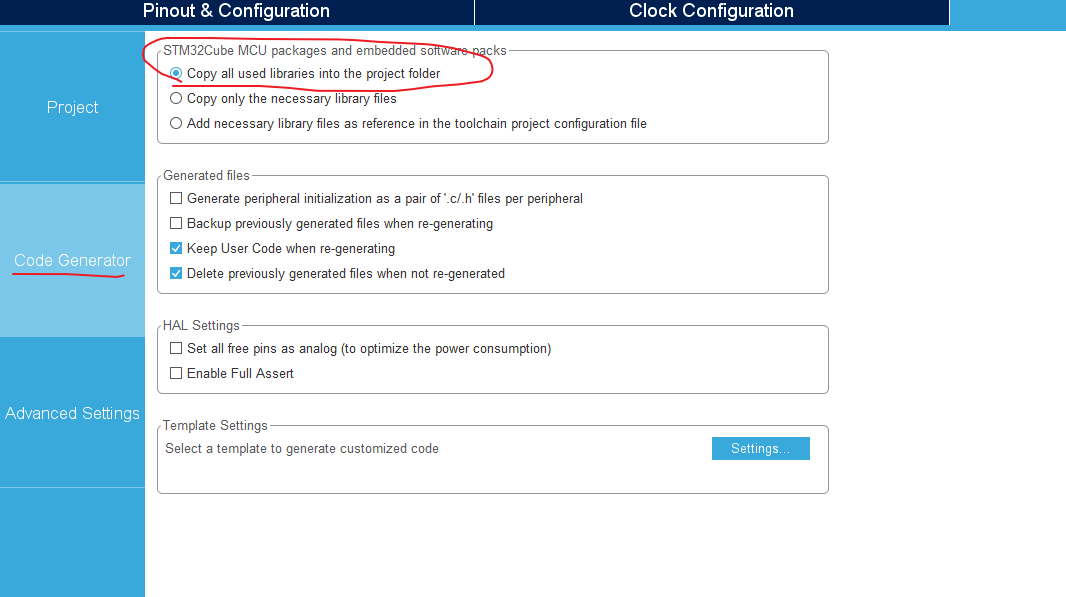
则可以在工程文件夹下找到所需要的的文件，文件目录结构与cubeMX下的路径相同

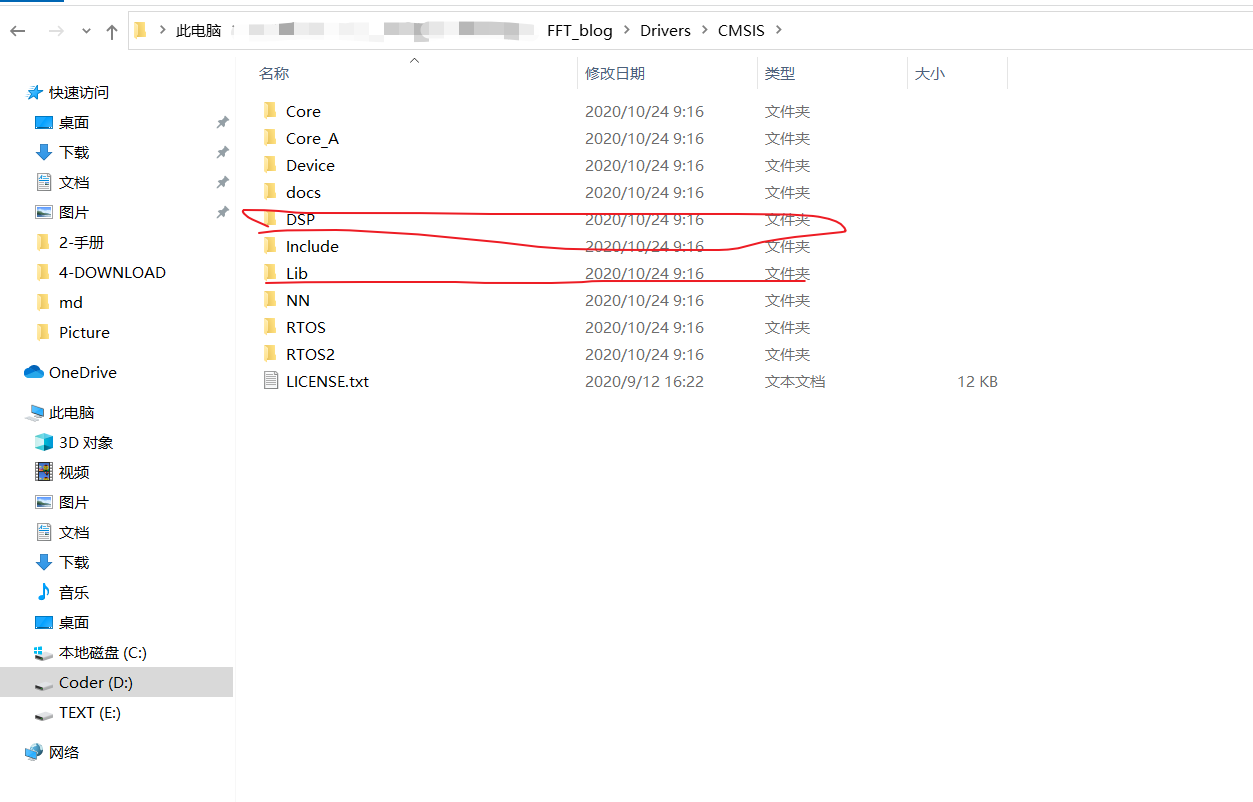
如果觉得上述操作过于麻烦，

可以使用cubeMX自带的例程模板，在此模板的基础上进行改进

DSP库的Example 位于：安装目录\STM32Cube\Repository\STM32Cube_FW_F4_V1.25.1\Drivers\CMSIS\DSP\Examples\

有ARM和GCC两个版本，这里以ARM为例，

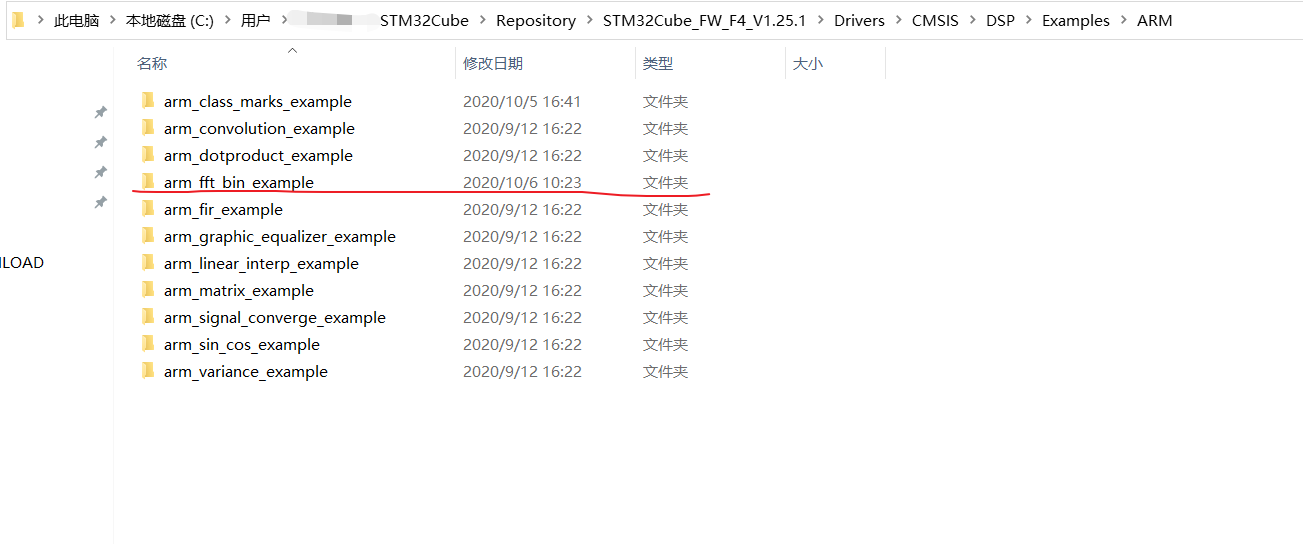
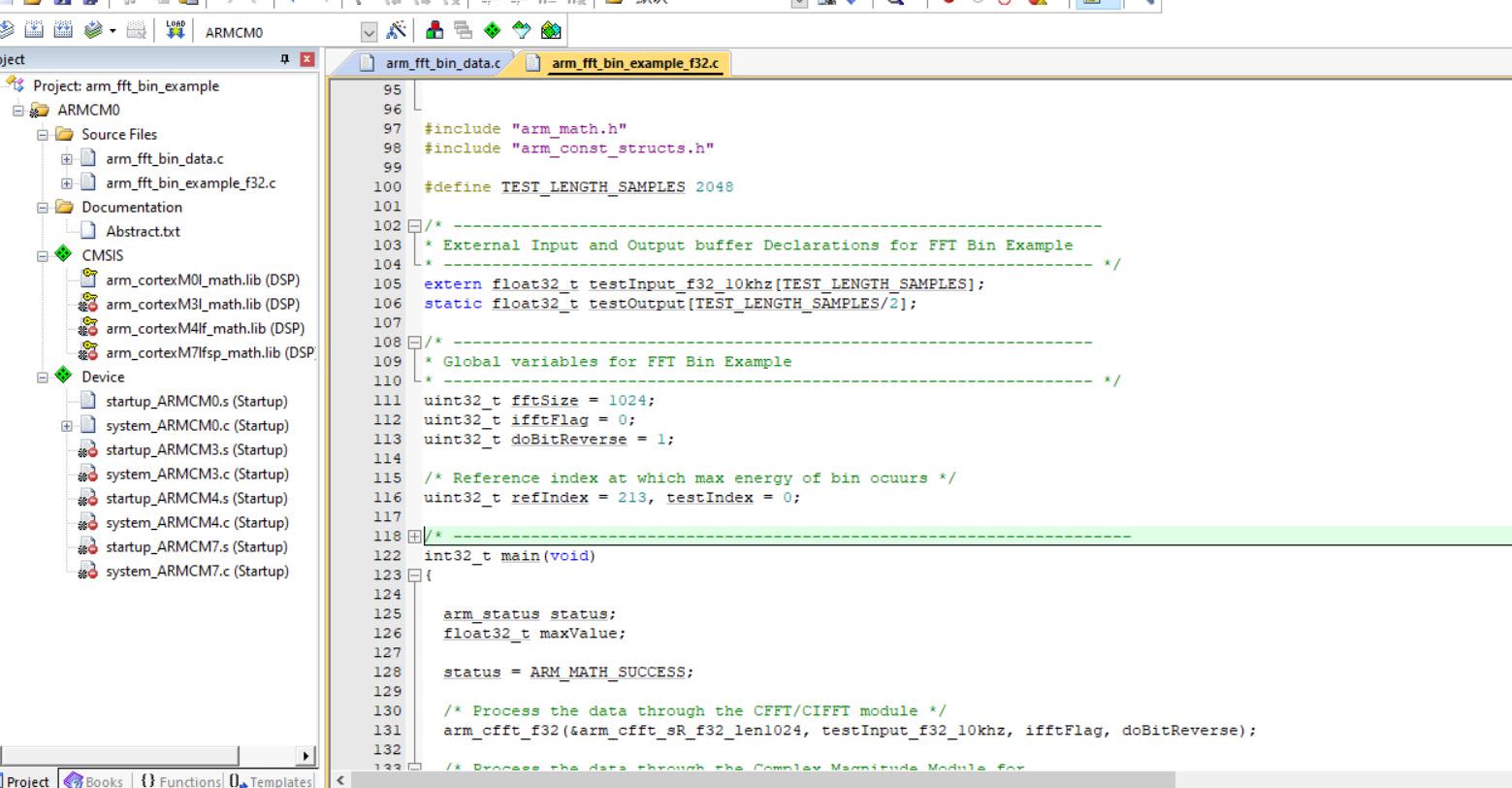
不过此工程并未未添加宏定义，且使用的cortexM0内核，需要做一定的修改。个人不推荐使用此文件构建工程，这个工程更适合与用来熟悉函数的用法和功能。

然后在已经配置好的工程中编写代码，测试一下

首先引入头文件，然后定义一些用到的量

/* Private includes ----------------------------------------------------------*/
/* USER CODE BEGIN Includes */
#include "arm_math.h"
#include "arm_const_structs.h"
/* USER CODE END Includes */

/* Private typedef -----------------------------------------------------------*/
/* USER CODE BEGIN PTD */
#define Half_FFT_LENGTH	64
#define FFT_LENGTH      128				// FFT长度，默认是1024点FFT


uint16_t ADC_Value[FFT_LENGTH]; 		// ADC转换结果
float fft_inputbuf[FFT_LENGTH*2];		// FFT输入数组
float fft_outputbuf[FFT_LENGTH];		// FFT输出数组
/* USER CODE END PTD */

然后编写FFT变换的函数

void FFT(void)
{
	int i = 0;
	
	for(i=0;i < FFT_LENGTH;i++)
	{
		fft_inputbuf[i*2] = ADC_Value[i];
		fft_inputbuf[2*i +1] = 0;
	}
	
	arm_cfft_f32(&arm_cfft_sR_f32_len128,fft_inputbuf,0,1); // 执行FFT变换，arm_cfft_sR_f32_len128为宏，定义旋转因子
	arm_cmplx_mag_f32(fft_inputbuf,fft_outputbuf,FFT_LENGTH);    // 把运算结果复数求模得幅值
}

这里要说明一下

DSP库提供的fft变换，是可以同时进行正反变换的，为了兼容反变换，我们在进行FFT时，要将虚部赋值为0，即fft_inputbuf的内容应该为：ADC_Value1, 0, ADC_Value2, 0 .... 有效的值只有fft_inputbuf长度的一半，要进行的FFT也只有fft_inputbuf的一半，所以，要进行1024点的fft变换，就需要输入2048长度的数组。

如果进行的是1024点的FFT变换，则得到1024长度的结果数组。

总谐波失真（THD）计算

首先，我们要知道经过FFT变换后得到的数组有什么物理意义，每个数组的值代表什么，这里直接说结论

\[设f_s 为采样频率，N为FFT点数（进行变换的FFT序列的长度），进行FFT变换后得数组下标为k的值代表的频率为f_k 则： \]

\[f_k = \frac{k}{N}*f_s \]

也就是说，如果ADC的采样频率为1024Hz 进行2048点的FFT变换，则FFT变换后数组下标为5的位置对应的频率为$$ f_5 = \frac{5}{1024} *2048 = 10hz$$ 也就是说，fft_outputbuf[5] 值的大小代表信号中10hz信号强度的大小。

明白了这个道理后，再来看如何计算总谐波失真，根据公式：

\[ THD = \frac{\sqrt{\sum_{n=0}^{\infty}{G_{n}^{2}}}}{G_0} (G_0为基波，G_n 为高次谐波) \]

我们需要知道基波和谐波分量的大小，就可以轻易的计算出来THD的大小

对E题来说，信号的频率是固定的，只要采样频率\(f_s\)固定，点数N固定就可以很方便的得到基波分量，和谐波分量的位置

可以通过定时器来产生固定频率的采样信号，由于原信号为1k，谐波分量为2k、3k、4k、5k、6k... 采样频率应该大于最高频率的3-5倍，

但，本题中我在题目中加入了波形显示，根据采样算出来的30k的采样信号在LCD上的显示效果不好，同时又为了方便计算，我的采样频率选择为102.4kHz, 通过计算可以知道，fft_outputbuf[10]的大小就是基波分量的大小，二次谐波在fft_outputbuf[20]、三次谐波在fft_ouptubuf[30]... 依次类推， 这样总谐波失真就可以很简单的计算出来了。

void THD(void)
{
	thd_basic = fft_outputbuf[10];

	u[0] = fft_outputbuf[20];
	u[1] = fft_outputbuf[30];
	u[2] = fft_outputbuf[40];
	u[3] = fft_outputbuf[50];
	u[4] = fft_outputbuf[60];

	arm_power_f32(&u[0], 4, &sum);
	arm_sqrt_f32(sum, &thd_high);

	THD = thd_high / thd_basic;

}