Matlab 拟合工具APP的使用以及模型评估参数介绍

在数值分析中，插值和拟合是常用的两种建模方式，对数据样本（输入和输出）进行分析进而得到相应的结果。

Matlab拟合工具

1. 拟合的意义和来源

2. 自带APP工具的使用

2.1. 给定样本构建模型

2.2. Matlab自带拟合工具 Curve fitting

2.8. fitresult值的类型CFIT介绍以及具体含义

2.9. Generated Code Introduce（2.7的补充）

3. 模型评估参数指标（SSE、MSE、RMSE、R_Square等等）

4.参考资料

1.拟合的来源

如同大脑一样学习一样，只有老师教授（输入）学生才能够掌握知识并将知识输出。在计算机人工智能机器学习中

也是相同道理。给定一定数量的样本（输入输出），得到关于该研究对象的模型的过承诺就成为拟合（建模）。

拟合的方式：有抛物线，多项式，线性拟合等等方式。

手算过程：可以参考之前写的一篇文章：最小二乘法原理及其应用

2.Matlab拟合工具使用

2.1. 给定样本构建模型

 clc;clear;
 x = [0.2 0.3 0.3 0.8 1.4 2.5 1.6 3.0 1.8 1.9];
 y = [2.7833 1.4555 1.6666 2.4321 1.9882 1.7822 0.9999 0.3233 1.4321 0.9212];

2.2. Matlab自带拟合工具 curve fitting

2.3. 加载数据

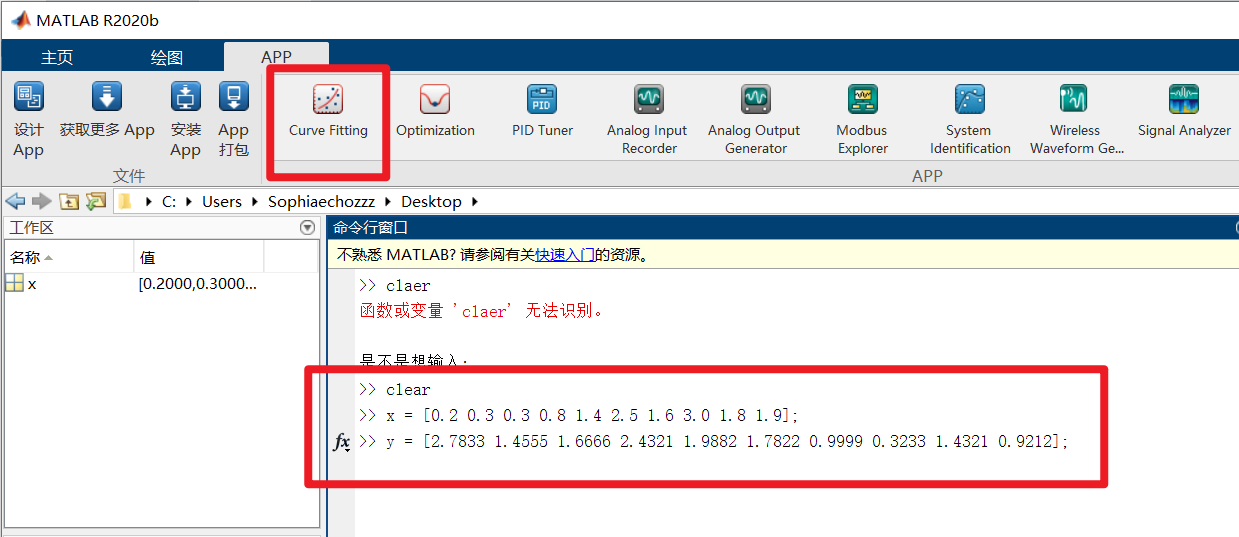
路径：Matlab-APP-Curve fitting

为x data 和y data 加载数据，由原先输入x、y可以得到。

2.4. 选择拟合曲线类型

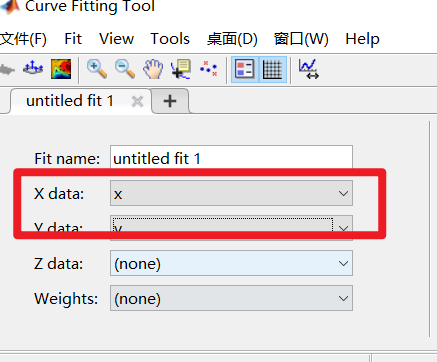
选择拟合类型fit type 和拟合的方式，通过fit options 限定拟合的起始点参数和参数的上下限。

工具箱提供的拟合类型：

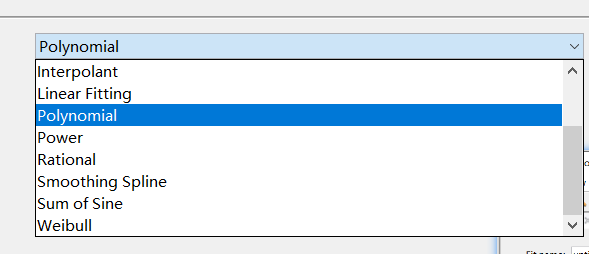
参数详细介绍：

Custom Equations：用户自定义的函数类型
Exponential：指数逼近，有两种类型 a*exp（b*x）、a*exp(b*x)+c*exp(d*x);
Fourier: 傅里叶逼近，有7中类型，基础型是a0+a1*cos(x*w)+b1*sin(x*w);
Guassian:高斯逼近，有8种类型，基础型是a1*exp（-（（x-b1）/c1）^2）;
Interpolant: 插值逼近，该方法的优势在于会连接所有点，而使其SSE为0,R-square为1

四种类型：Nearest neighbor、Linear、Cubic、Spape-preserving(PCHIP);

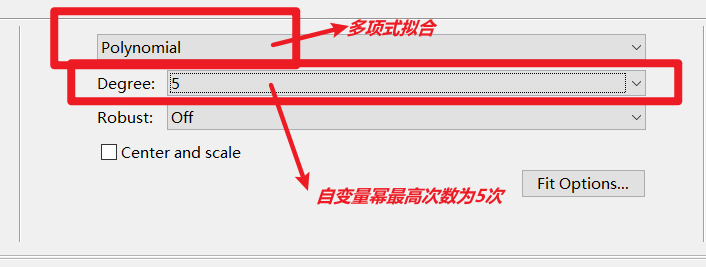
polynomial:多项式逼近，自己定义多项式的幂的等级
Power：幂逼近，有两种类型，a*x^b、a*x^b+c;
Smoothing spline：平滑逼近，该方法的会尽可能逼近所有点，使其SSE尽可能逼近0，R-square尽可能逼近1.
Rational: 有理数逼近
Sum of Sin Function:正弦函数逼近，有8种类型，基础型是a1*sin（k*x+b1）；

2.5. 曲线拟合

左侧是拟合的结果，右侧是拟合的效果图。其实SSE\R-square\DFE是拟合的评价参数，coefficiency是其系数。

2.6. 拟合结果分析

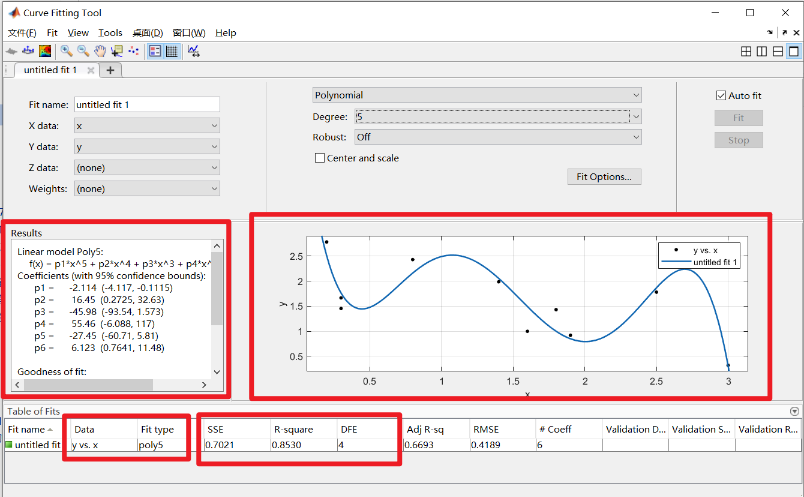
在左侧的Result中显示拟合模型，参数以及拟合效果；

拟合效果评测标准函数（goodness of fit）

SSE: 拟合误差平方和，接近0，表示与数据拟合的好，但是要小心过拟合；
R-Square：实现测量数据与推理数据之间的相关系数平方值，趋近于1较好；
RMSE: 均方差；
Adjusted R-square（确定系数）

2.7. 输出拟合参数

（1）只显示拟合图像，可以点击文件-Print to figure

（2）导出拟合后的曲线数据，点击文件-generate code

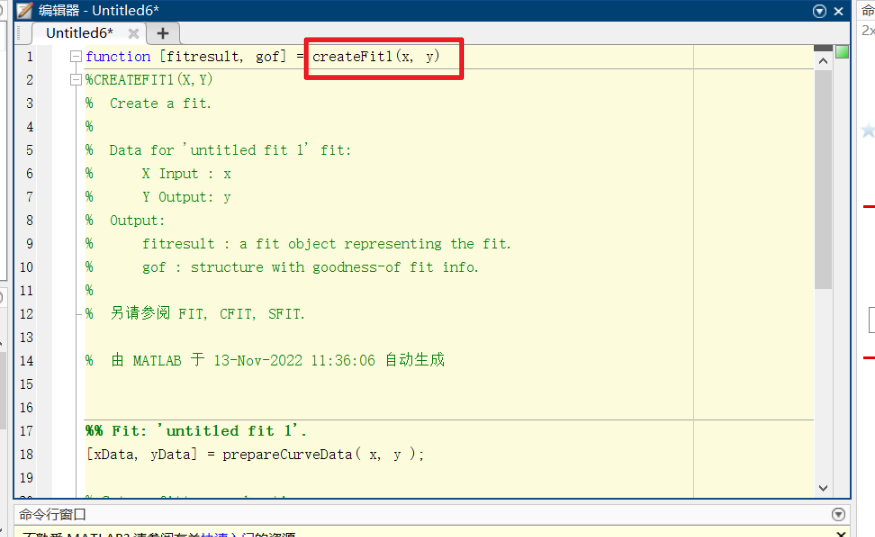
1.产生一个createFit1的函数，如下图所示

具体介绍就是函数名为createFit，输入参数为x、y,输出参数为fitresult 和gof.

其中fitresult 包含求解系数，gof代表拟合评价。

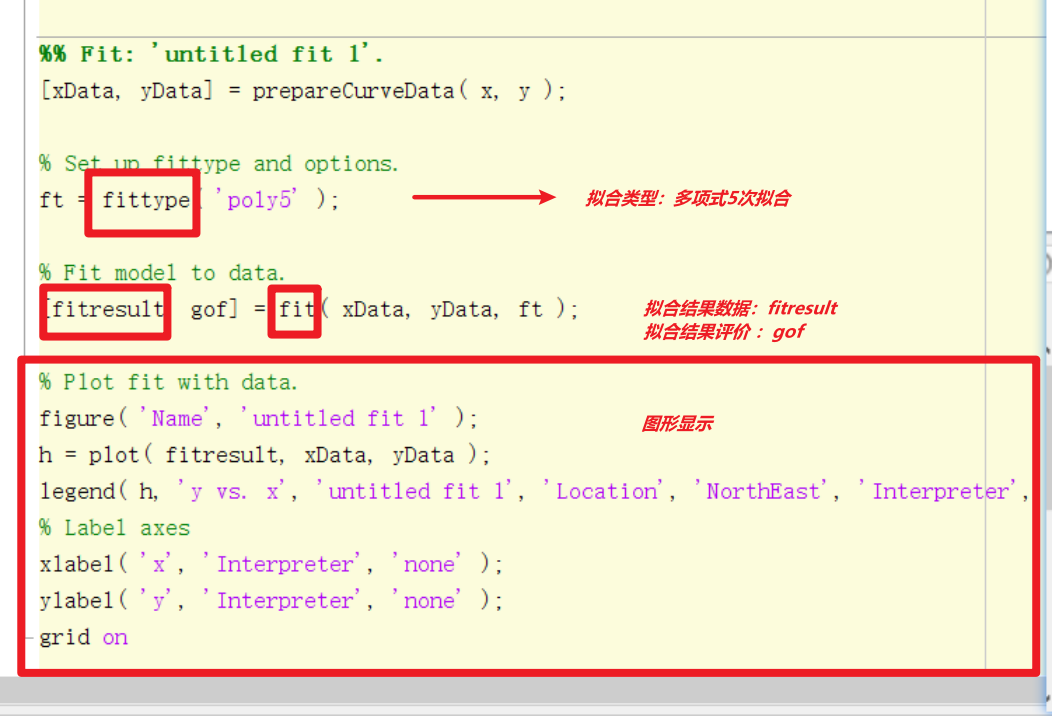
2.主要代码介绍

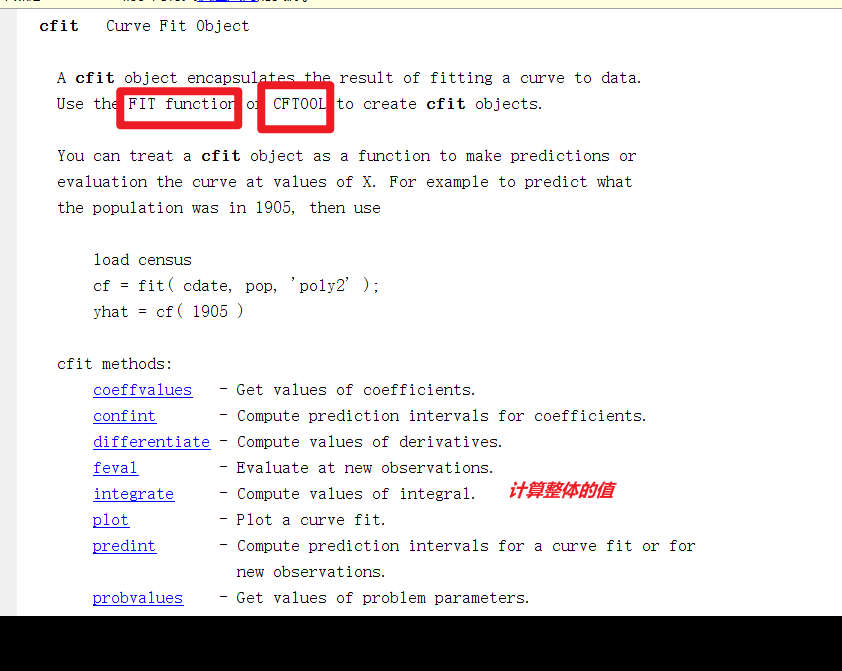
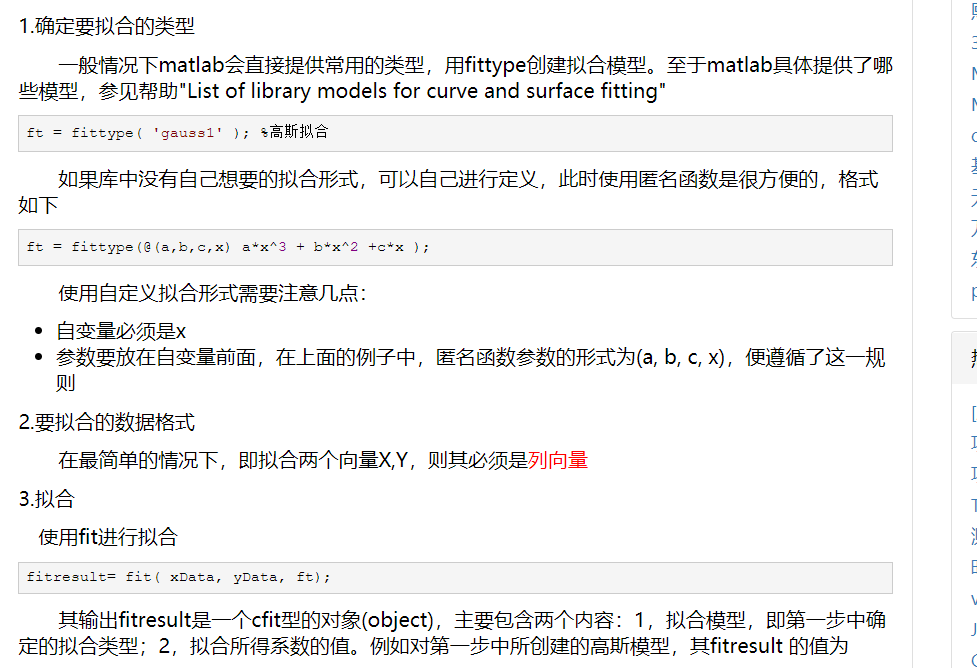
2.8. fitresult值的类型CFIT介绍以及具体含义

首先在工作区双击fitresult，得到变量的类型CFIT,以及相应的值的介绍，如下所示。

fitresult介绍：

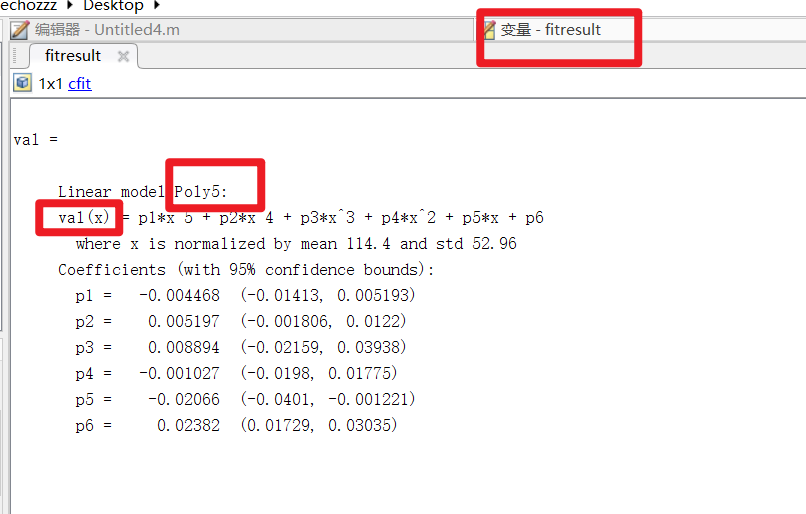
CFIT介绍

2.9.Generated Code Introduce

3. 模型评估参数指标

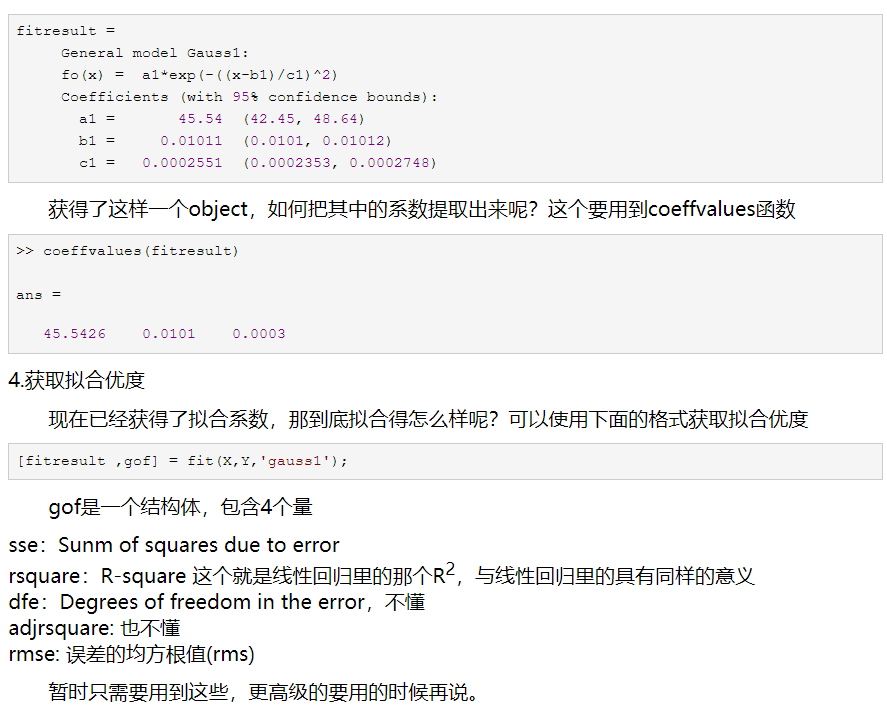
种类：SSE、SSR、SST、R_square、MSE、RMSE

方差：是概率论和数理统计中的？？？？？？？？？？？？？？？

一、SSE(和方差、误差平方和)：The sum of squares due to error

该统计参数计算的是拟合数据和原始数据对应点的误差的平方和

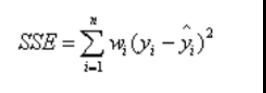
二、MSE (均方差)：Mean squared error

该统计参数是预测数据和原始数据对应点误差的平方和的均值，即SSE/n (其中n代表数据的个数)

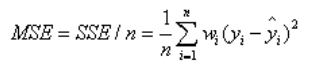
三、RMSE(均方根，回归系统的拟合标准差)：Root mean squared error

该设计参数，也叫回归系统的拟合标准差,是MSE的平方根，即

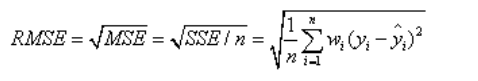
以上所有误差，都是点对点 的误差（预测值和原始值之间的误差）

在确定系数前，我们需要介绍另外两个参数，即SSR\SST

SSR：Sum of squares of the regression

SST: Total sum of squares

四、 R-square

SST = SSR +SSE ？？？（不理解）

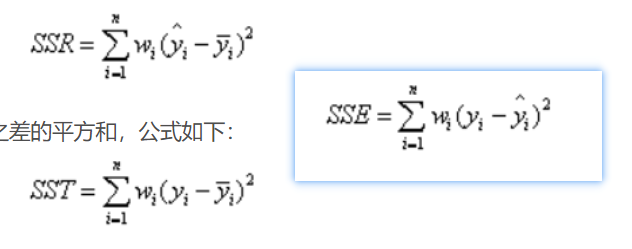
而 R-Square = SSR/SST =( SST -SSE)/SST = 1- SSE/SST

确定系数是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数的”正常取值范围是

[0 1],越接近1，表明方程的变量对Y的解释能力越强，这个模型对于数据的拟合也较好。

详细参考：https://www.jianshu.com/p/bb731e1e393f

五、 Adjusted R-Square

无，不了解，是统计学中的内容，暂且放下。

详情视频教程（英文）：https://www.bilibili.com/video/BV1DR4y1F7Rq/?spm_id_from=333.788.recommend_more_video.-1&vd_source=561934207ddd71d981d0f59933b055e6

参考资料：

1. Matlab Tool Usage introduction（Super Explicit）

https://blog.csdn.net/didi_ya/article/details/119042304?ops_request_misc=&request_id=&biz_id=102&utm_term=Matlab%E6%8B%9F%E5%90%88%E5%B7%A5%E5%85%B7&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-1-119042304.142^v63^js_top,201^v3^add_ask,213^v2^t3_esquery_v3&spm=1018.2226.3001.4187

2. Assignment Parameter Introduction

https://blog.csdn.net/qq_42261630/article/details/103475422

（Matlab中的 SSE、MSE、RMSE、R-square、Adjusted R-square）

https://www.jianshu.com/p/bb731e1e393f（R-Square 的详细介绍）

https://blog.csdn.net/sirow/article/details/109630056（线性回归模型评估参数）

3. Matlab Paragramming Code introduction（自己不用app如何写代码）

http://t.zoukankan.com/CherryWull-p-5574277.html

时间：20221113/14:30:07

posted @ 2022-11-16 14:40 InitForever 阅读(3262) 评论(0) 编辑收藏举报

刷新页面返回顶部

InitialForever

记录数学、嵌入式开发、通讯协议、图像处理机器视觉等学习笔记

Matlab 拟合工具APP的使用以及模型评估参数介绍

公告