线性代数基础知识 学习笔记
简要概述:万物皆矩阵!
由齐次/非齐次线性方程组讨论解的存在性引出秩的概念和线性相关和线性无关,由线性
相关和线性无关引出基的概念,并通过斯密特正交化引出单位正交基,其作用是在方向投影等于
其本身大小,正交矩阵作用于向量不改变模(范数)的大小;通过对矩阵分解引入特征值和特征
向量的概念,特征值是矩阵的特性,唯一且不变,而其对应的特征向量不定,因为我们取得只是
齐次方程的一个解,而这个解对应一个基础解系。特别的,实对称矩阵不同特征值所对应的特征
向量一定正交;引入相似矩阵,实对称矩阵一定可以通过相似对角化。相似矩阵的作用是将矩阵
的特征值和特征向量全部表示出来的方式。
Content
- 1 .Determination(Det)
- 2. Homogeneous equation and non-homogeneous equation of solution
- 3. Linear correlation and Linear independence
- 4. Solution Vector
- 5. Base solution group of linear equation group(线性方程组的基础解系)
- 6. Engivalue and Engivector
- 7. Similar Matrics
- 8. Real Symmetric Matrix and Matrix of a quadratic form
- Vital understanding for Engivalue and Engivector Matrix(特征值和特征向量深层次理解)
- Definition
- Example
- Some Quesion about engivalue and engivector
- Type of Matrix introduction
- Refrence
1. Determinant
Defination:对于矩阵A(nxn),行列式等于不同行不同列n个数的乘积之和。
=======假设原先行列式的值: |D|=A=========================================
性质1:任意两行互换,|D|=-A
性质2:把行列式中A的某行(或列)中元素同乘一数加到另一行,结果任为A。
性质3:A = A^T,由行列式性质可知
性质4:某行同乘K,结果为K*A
性质5:任意两行相同,行列式为0
应用:(1)求解非线性方程组,行列式|D|≠0,这非齐次方程有唯一解。
(2)求解齐次方程,行列式|D|=0 ,则方程存在非零解。
(3) |A|=0,可得:
1.A的行向量线性相关
2.A的列向量线性相关
3.方程组Ax =0 存在非零解
4.A的秩小于n
5.A不可逆
2. Homogeneous equation and non-homogeneous equation of solution
5.2.1 齐次方程(Homogeneous equation),则 A * X = 0, 其中A是nxn矩阵,X是向量(x1,x2,x3,x4,...)
For example:
a11*x1+a12*x2+a13*x3+...a1n*xn = 0;
a21*x1+a22*x2+a23*x3+...a2n*xn = 0;
...
an1*x1+an2*x2+an3*x3+...ann*xn = 0;
Coefficienct Matrix A =
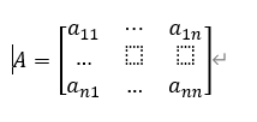
Vector variable X =
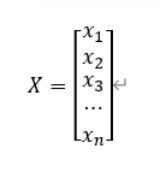
Compose: A*X =0; (A和X都加粗表示矩阵和向量)
特别的,齐次方程一定有解,解为0,存在非零解的条件是 |A|= 0(线性相关)or Rank(A)<n。
5.2.2 非齐次方程(Non-homogeneous equation)
Expression: A * X =B
Existence Situation of Solution:
(1)无解 |A| = 0,化为上三角或下三角行列式,行列式中存在相同行,在B右边值非0,则无解( rank(A) <rank(A,b))
(2)有唯一解,rank(A(nxn)) = n = rank(A,B);
(3)有无穷多个解 rank(A)=rank(A,b) < n
这里涉及矩阵秩的概念,矩阵的秩的定义:是其行向量或列向量的极大无关组中包含向量的个数(行秩和列秩中的最小值)。
3. Linear correlation and Linear independence
根据齐次方程或非齐次方程解的类型,可以引出线性相关和线性无关的概念。
线性相关:设 向量组A:{a1,a2,a3,...},若存在a1 = b1*a2+b2*a3+...bn*an,即an可以由其他向量表示,这被认为线性相关。
几何意义:如向量B:(线性无关)

代表基坐标(1,0,0) ,(0,1,0),(0,0,1),这乘上向量X(x1,x2,x3),代表线性变换后的结果为在这个坐标系下对
X进行变换的结果为(x1,x2,x3)。
4. Solution Vector
设R(A)=r;
若B是Ax = 0 的解向量,则B是Ax = 0的基础解析的子集,B能被AX=0的基础解析线性表示。这R(B)<=R(A) = n -r
5. Base solution group of linear equation group
(5.1)设齐次线性方程组中AX =0 的 基础解析为 {b1,b2,b3...bn}
则该方程的基础解析为x =a11*b1+a22*b2+...ann*bn
(5.2)设非齐次线性方程组 AX =B的基础解析为{c1,c2,c3...cn}
则该方程的基础解析为x = 齐次方程的基础解系 + 非齐次方程的一个解
证明:
设 AX = B的解为ξ1,ξ2,则ξ1-ξ2是齐次方程AX =0的解,我们可以求得齐次方程的基础解析
等于C1v1+C2v2+...CVvn = ξ1-ξ2
即ξ1 =(C1v1+C2v2+...CVvn) + ξ2
即非齐次方程的解 = 齐次方程的解 + 非齐次方程的一个特解。
求非齐次方程组的通解的一般方法:
1.初等变换为行阶梯形,判断是否有解,即R(A)=R(A,b)
2.若存在,则化为行最简式。
3.列方程组,通常格式为 = 齐次方程组的基础解系 + 非齐次方程组的一个解
4.检验:通过A的R(A),可判断齐次方程组的基础解系的个数为Rs= n - r.
例子:求非齐次线性方程组的通解
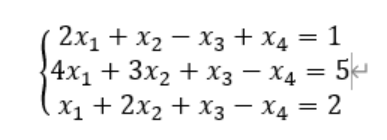 的通解
的通解
则A的系数矩阵为
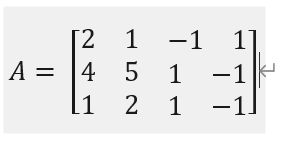
对A,b做初等变换
\\ 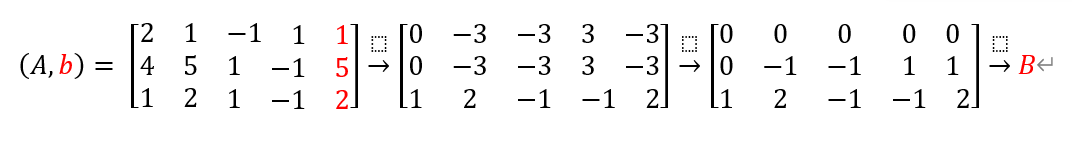
因为R(A)=R(A,b) =2<4,则方程存在无数多个解(意味着方程组的个数小于未知数的个数)
则
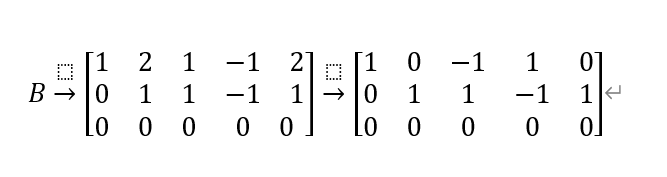
则对应线性方程组为
则 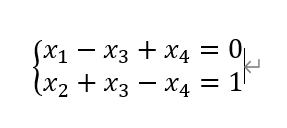
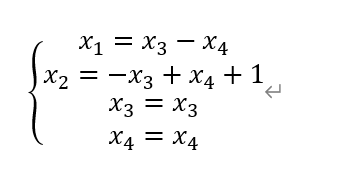
接下来,将x3和x4 看成常数提出,则非齐次方程组的基础解系
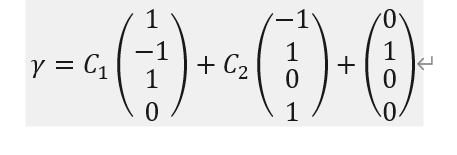
6. Engivalue and Engivector:
6.1 Defination in Math:
给定的矩阵A(方阵),如果有一个向量v,使得矩阵A作用于v之后(即A和v相乘),得到的新向量和v
任然保持在同一条直线上,像下面这样:
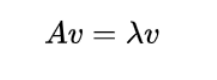
那么就称向量v是矩阵A的一个特征向量,而lmd就是特征向量v对应的特征值(一个特征向量一定对应
一个特征值)矩阵就是线性变换(nxn维度--->nx1维度,就是可以从矩阵中取出向量和特征值),向量v
在经过矩阵A这个线性变换之后,新向量和原来的向量v任然保持在同一条直线上,也就是说这个变换只是
把向量v的长度进行了改变而保持方向的不变(在特征值是负数的情况下,新向量的方向是原来方向的反向
,即180°反方向。)
6.2 Relevant Conclusion:
1. 矩阵A对角线之和等于特征值的和
2. 矩阵A对角线之积等于 矩阵A的行列式
Certification:
设A为可逆的方阵
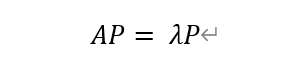
移位操作
![]()
如果使得方程有解,则行列式 |A-λE| = 0,得到结果
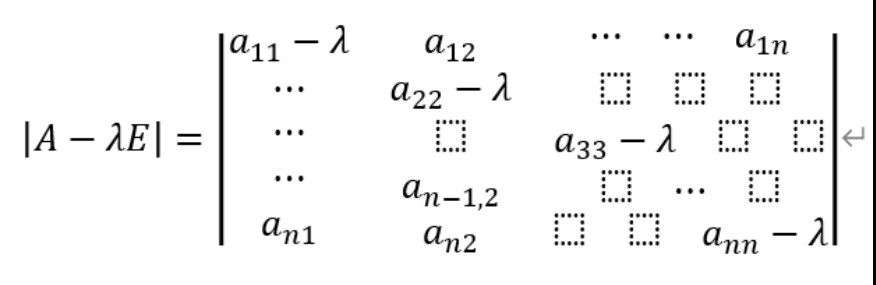
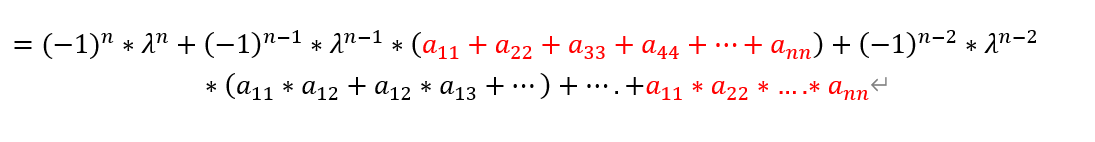
则根据韦达定理,根之和(特征值λ解之和)= a11+a22+a33+...+ann
特别的,当λ =0 时,行列式|A| = a11*a22*a33*....ann
END
6.3 About Engivalue and Engivector Conclusion
(1)Power: A^(k)*P = λ^(k)*p
(2)Inverse Matrix: A^(-1)*P = λ^(-1)*p
(3)Companion Matrix:(A*)*P =|A|* λ^(-1)*P
(4)Transfom Matrix:A^(T)*P = λ*P
(5)Function : f(A)*P = f(λ)*P
6.4 追问精神
(1)为什么N阶矩阵一定有n个特征值?
根据代数定理,n次多项式有且只有n个根,由行列式的性质可知,最高可展成n项,最低0次幂。
f(λ) = |A -λ*E|= 存在λ,且有n个这样的λ。(可能都相同,可能都不同)
(2)AP =λP,若使P存在非零解,
then R(A -λP)<n
or |A-λE| =0
(3)特征值和特征向量的应用
关于理解特征向量,主要应用于图像处理中。如下图所示。
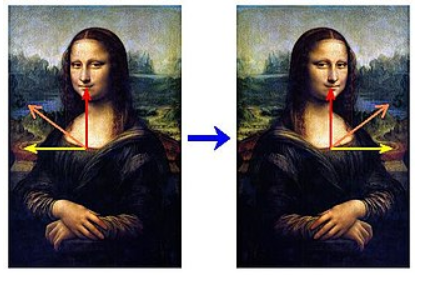
当蒙娜丽莎的图像左右翻转时,中间垂直的红色向量的方向保持不变。而水平方向上黄色的向量的方向
完全反转,因此它们都是左右翻转变换的特征向量。红色向量长度不变,其特征值为1.黄色向量的长度也不变
但方向变了,其特征值为-1.
橙色向量在反转后和原来的向量不在同一条直线上,因此不是特征向量。
7. Similar Matrices(Square Matrix)
Defination:
If P^(-1)*A*P = B ,then A ~B .
Relevant Property:(IF A Similar as B)
(1)Engi-polynomial not Change :|A - λE| = |B - λE |
(2) Engivalue not Change
(3)Determination not Change :|A| = |B| = λ1+λ2+...λn
(4)Trace of Matrix not Change:trA =trB=λ1+λ2+...λn = 矩阵对角线之和
(5)Rank not Change : rank(A) = rank(B), 初等变换性质决定
Quesion:
How to find similar matrics for A ?
(1)与零矩阵相似的只有零矩阵
(2)与单位矩阵相似的只有单位矩阵
(3)与数量矩阵相似的只有它自己
Why propose this quesion? introduce diagonalization for matrix.
(1) n阶矩阵A与对角矩阵相似的充分必要条件 是A有n个 线性无关的特征向量。
Certification:
A(P1,P2,P3,...Pn) = (P1,P2,P3,...Pn)*diag(λ1,λ2,λ3,...λn)
∵ p可逆,则
(A*P1,A8P2,A*P3,...A*Pn) = (P1*λ1,P2*λ2,....,Pn*λn)
由之前的特征值和特征向量知识可知,
(λ1,λ2,λ3,...λn)是A的特征值
(P1,P2,P3,...Pn)是A的特征向量
(2) 方阵A 的n个特征值有 相同的重数,则方阵A能对角化的充分必要条件是
*每一个K重特征值能够确定K个线性无关的特征向量。
*(A-λE)*x = 0的解空间的维数也是K
*R(A-λE) = n -K
APPLICATION:
(1)求解矩阵的高次幂
存在A和P,使得P^(-1)*A*P =√
则A = P*√*P^(-1) ===由特征值幂的性质
A^n = P*√^(n)*P^(-1) ;
(2)利用特征值求行列式
|A| = λ1*λ2*λ3*...*λn ;
(3)判断是否可逆,由(2)可知
(4)判断矩阵是否相似,只有求出各自的对角,对角相似就相似。
8. Real symmetric matrix and Matrix of a quadratic form
Real symmetric matrix:
Defination : 就是矩阵内元素都是实数,其次是对称的(n阶就是N BY N)
Attribution1:实对称矩阵的两个不同的特征值所对应的特征向量是正交的。(特征向量线性无关)
Attribution2 :任何实对称矩阵可以通过正交变换将其对角化。
更多性质如下,摘自百度百科。

Vital understanding for Engivalue and Engivector Matrix
(特征值和特征向量深层次理解)
线性代数的最后,我们都学会矩阵的特征值分解,我们知道一个方阵A经过特征值分解后就得到特征向量和特征值。
那么,这个所谓的特征值和特征向量如何理解呢?
书本上一上来就给这个公式:
Ax = λx,其中x 是一个向量
从公式角度理解,一个矩阵乘上这个向量 等于 一个数乘上这个向量。
特征这个词语来自德语,engen vector,本义是在“本身固有的,本质的”。几何意义就是一个矩阵
乘上向量等于 一个数乘上向量(在向量方向的拉伸压缩或不变)。
从实际应用角度,图像处理就应用到特征值分解。我们都知道图像是由一个个像素组成。假设有一个200x200
的图像,对这个图像矩阵的特征值分解,其实是在提取这个图像中的特征,这些提取出来的特征是一个个向量,即对应
着特征向量。在这个200x200矩阵分解之后,会得到一个200x200的特征向量组成的矩阵Q以及一个200x200的只有对角线
元素不为0的矩阵E,这个矩阵E对角线上元素就是该矩阵的特征值,而且还是按照大小排列,也就是该该特征值200个就是
图像的200个特征,这200个特征的重要性用200个数字表示,这200个数字存放在对角矩阵E中.在实际中我们发现,200个
特征,如果数值很小,对图像的影响就可忽略不计。
根据上述描述,我们知道图像矩阵A特征值分解后可以得到矩阵Q和矩阵E:(在相似矩阵这一章节描述过,见Matlab
learning notes1(1))
A = QEQ^(-1)
那么反推,把右边三个矩阵相乘肯定能得到矩阵A.既然已经知道矩阵E中只有数值较大的比较重要,那不妨将矩阵E中对角
线前20个保留,其余都设置为0,即只取图像的前20个主要特征来恢复图像,剩下的全部舍弃,看看此时会发生什么,
如下图所示。
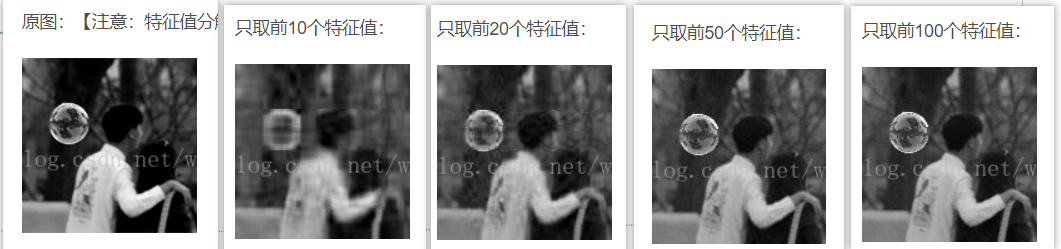
通过上图我们知道,在只取20个特征和特征向量对图像进行恢复时候,基本上已经可以看到图像的大体轮廓了,而
取到前50的时候,几乎已经和原图无差异。通过上述例子可以形象的理解矩阵的特征值和特征向量的作用。
注:特征值分解必须是nxn的方阵,如果不是行列相等的矩阵,请使用奇异值分解(这个在硕士课程 矩阵论上有)
1.特征值和特征向量什么关系?
在本节定义中讲过,这里不重复,特征值是矩阵固有的,是唯一确定的,特征向量不唯一。
因为如果手动算过都知道,我们取的特征向量只是齐次方程组的基础解析中的一个,并不唯一。
但特征值是特征多项式的根,所以是唯一确定的。
2.一个特征值有几个特征向量?
一个特征值对应无数个特征向量。
3.不同特征值所对应的特征向量是否正交?
实对称矩阵的特征值所对应的特征向量正交。
详细证明见:https://blog.csdn.net/qq_37430422/article/details/106254745
(1)实数领域:(real number range)
(1)单位unit matrix
(2)对角矩阵(相似矩阵 正交化)
(3)正交矩阵 A^T*A =E(斯密特正交化,矩阵分解上挺好的) (复数领域:酉矩阵 A^H*A = E)
(4)逆矩阵 A^-1*A =E (求解线性方程组)
(5)伴随矩阵 A*
(6)单位上/下三角矩阵(upper/down Matrix)
(7)对称矩阵(特征值所对应的特征向量正交)(实对称矩阵是Hermite 矩阵特例,在虚部为0时候成立)
(8)旋转矩阵
(2)复数领域:(complex range)
(1)共轭矩阵(相对于实数中的对称矩阵)
定义:埃尔米特矩阵又称自共轭矩阵、Hermite阵。Hermite阵中每一个第i行第j列的元素都与第j行第i列的元素的共轭相等(然而矩阵A的共轭矩阵并非Hermite阵)。
共轭:就是矩阵每个元素都取共轭(实部不变,虚部取负)
转置:就是把矩阵的每个元素按左上到右下的所有元素对称调换过来。
共轭转置:就是先取共轭,再取转置。
(2)Hermite matrix 与其相对的是实对称矩阵
(3) 酉矩阵 与其相对的是正交矩阵
(4)正规矩阵 A^H*A =A*A^H
Refence :
(1)https://blog.csdn.net/woainishifu/article/details/76418176 (About engivalue and engivector
application and understanding) (特征值和特征向量的理解)
(2)https://blog.csdn.net/qq_37430422/article/details/106254745 (实对称矩阵不同特征值所对应的特征向量一定正交)
(3)https://zhuanlan.zhihu.com/p/416913409 (范数的理解 =模)
(4)https://blog.csdn.net/qq_44884706/article/details/89489189(正交矩阵的理解)
时间:20220531 知行合一,方能走的长远



