浅谈 超平面(Hyperplane)
大纲
1.超平面的定义
维基百科:超平面是n维欧式空间中余维度等于一的线性子空间,也就是必须是(n-1)维度。
n维空间超平面由以下方程确定:
![]()
其中,w和x都是N维列向量,x为平面上的点,w为平面上的法向量,b为实数:代表原点到超平面的距离
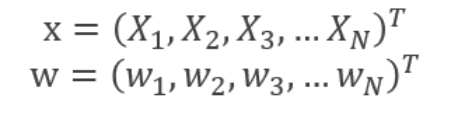
则(x1,x2,x3,....xn)*(w1,w2,w3,...wn)+b = w1*x1+w2*x2+......+wn*xn+b=0
特别的,对于3维的超平面是 w1*x1+w2*x2+w3*x3 +b = 0 (平面:ax+by+cz+d=0)
对于2维的超平面是 w1*x1+w2*x2+b = 0 (线:ax+by+c=0)
2.1 超平面的直观理解
直观上理解的超平面是样本空间中维度大于3,但实际上,超平面可以是点,线,面。
- 对于点而言,将线段分成两段(0维的点可以将1维的线分成两部分)
- 对于线而言,将面分成两面(1维的线可以将2维的面分成两部分)
- 对于面而言,将体分成两块(2维的面可以将3维的体分成两部分)
2.2 三维空间的超平面
在高中时候我们学过平面的方程,平面在我们“直观”的理解中就是在三维空间中的一张面
平面A: Ax+By+Cz+D=0
其中n=(A,B,C)^T是平面A方程的法向量,x,y,z分别是在三维笛卡尔坐标系下的维度,D是系数
平面性质:
1.方程是线性的
2.方程数量是1
超平面是纯粹的数学概念,不是物理概念,它是平面中的直线、空间中的平面的推广,
只有当维度大于3,才能称为“超”平面。它的本质是 自由度比空间维度小1。自由度的概
可以简单理解为至少要给定多少分量的值才能确定一个点。例如在三维空间中,只要给定
了(x,y,z)中任意两个分量,剩下的一个的值就确定了,先确定值的两个分量是自由的。
2.3 从二维空间理解超平面
设R2(2维空间)中的点集 i=(x,y) 满足等式(点集相当于直线)
a*x+1/b*y+c =0 (1.1)
则直线L:
y = -a*b*x-c*b (1.2)
进一步,采用换元法 ,令t等于x,则
点集 i = (x,y)=(t,-a*b*t-c*b) = t*(1,-a*b)+(0,-c*b)
则直线L:是过(0,-c*b),方向为(1,-a*b)的直线L
这是,我们令 向量n=(a,1/b),则(1.1) 可以表示为 (数量积)
n*i + c =0 (1.3)
我们在直线L上取一点P0(x0,y0),则 n*P0+c = 0
则
c = n*P0 (1.4)
将(1.4)代回到(1.3)中得到 (1.5),即
n*i-n*P0 = 0 (1.5)
进一步化简
n*(i - P0)=0
则 n 与(i-P0)正交(n与(i-P0)均是向量,此时n是二维的,i、P0都是二维坐标)
即
n 是过P0(X0,Y0)该直线的法向量,如下图所示
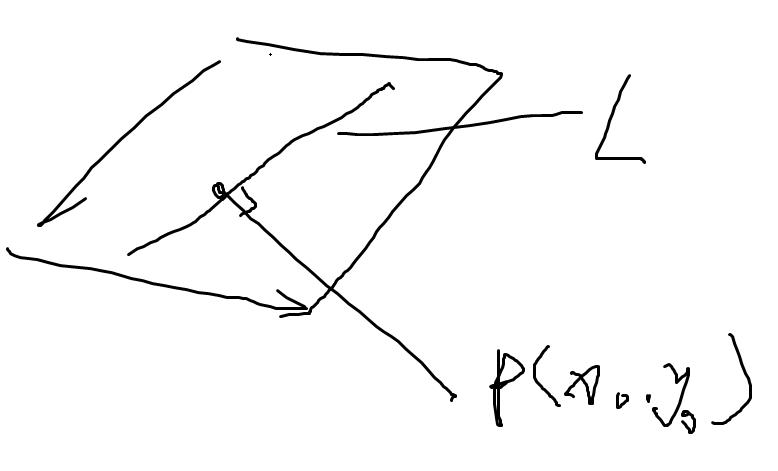
3. N维空间超平面的理解
这时候回头看第一节描述的超平面定义
![]()
给定向量空间Rn中的一个点P和一个非零向量n,满足
n*(i - P)=0
这里的n 就是w^T,点集i =(x,y)就是x,b就是n*P, P是直线L上的一点( 向量n为通过超平面的法向量)
人话说:给定向量空间Rn中的一点P和一个非零向量n,满足
n*(i - p) = 0
则称 点集i 为通过P 的超平面,向量n为通过超平面的法向量
4. 计算样本空间任意点到超平面的距离
样本空间中任意一点 x 到超平面的(w,b)的距离
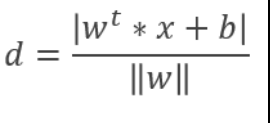
证明: 假设x`是 超平面上 任意一点
则满足
wt*x` + b =0
则
b = -wt*x`
则
wt*x - wt*x` = 0
则
wt*(x-x`) = 0
存在平面外一点x,则
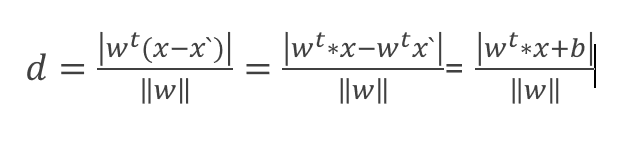
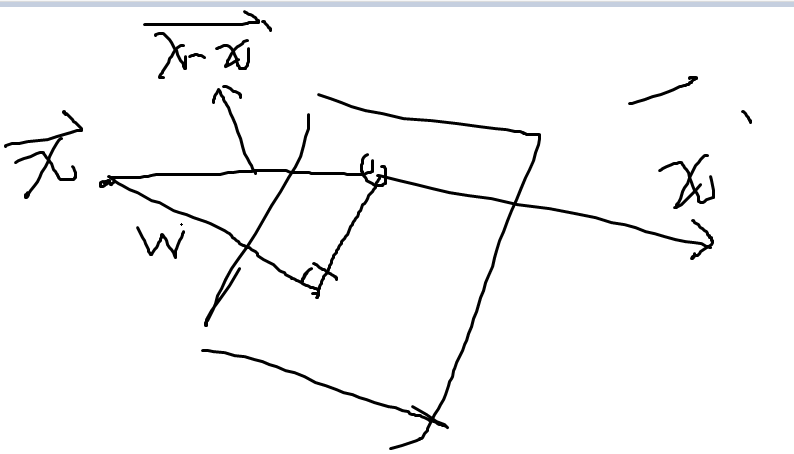
由下图可知,wt和(x-x`)都是矢量,则两者数量积/wt的模等于
(x-x`)投影在wt上的长度,即 平面外x到 超平面的距离。
5. 判断超平面的正反
一个超平面可以将它所在的空间分成两半,它的法向量指向的那一半的一面是它的正面,另一面是它的反面。
如果利用数学来判断的话,就用到法向量w。

如将距离公式中的分子绝对值去掉,则它可以为正或负,则它的值离原点越远,代表点离平面距离越远。
反之,越近。
时间:2021-0107



