随机数相关面试题(转)
当前面试中各大名企经常出现各种各样的概率类面试题。究其原因,我觉得是概率型面试题可以综合考查面试者的思维能力、应变能力、数学能力。在这里对各种类型的概率型题目进行了收集和总结,希望在自我总结的同时对大家有所帮助。
1、给你一个数组,设计一个既高效又公平的方法随机打乱这个数组(此题和洗牌算法的思想一致)
方法比较简单,基本思想是每次随机取一个数,然后把它交换到最后的位置。然后对前(n-1)个数使用递归的算法。
递归实现:
void suffle_dfs(int ar[], int n) { if(n<=1)return; swap(ar[n-1], ar[rand()%n]); shuffle_dfs(ar,n-1); }
非递归实现:
void suffle(int ar[], int n) { while(n>1){ swap(ar[n-1], ar[rand()%n]); n--; } }
注:此处假设rand()的返回结果远远大于n。
2、有一苹果,两个人抛硬币来决定谁吃这个苹果,先抛到正面者吃。问先抛者吃到苹果的概率是多少?
这种题目一看似乎答案就是1/2,但其实认真细想并没有那么简单。
给所有的抛硬币操作从1开始编号,显然先抛者只可能在奇数(1,3,5,7…)次抛硬币得到苹果,而后抛只可能在偶数次(2,4,6,8…)抛硬币得到苹果。设先抛者得到苹果的概率为p,第1次抛硬币得到苹果的概率为1/2,在第3次(3,5,7…)以后得到苹果的概率为p/4(这是因为这种只有在第1次和第2次抛硬币都没有抛到正面(概率为1/4=1/2*1/2)的时候才有可能发生,而且此时先抛者在此面临和开始相同的局面)。所以可以列出等式p=1/2+p/4,p=2/3。
现在答案已经很明确了,所以大家平时要注意不要这样被人骗了,当然也不能去骗别人,哈哈~
3、一条长度为l的线段,随机在其上选2个点,将线段分为3段,问这3个子段能组成一个三角形的概率是多少?
设随机选取的两个数为x,y,并令y>x,则把长度为1的线段截得的三段长度为x, y-x ,1-y,根据三角形两边和大于第三边以及两边之差小于第三边的定理,可以列出方程组 y>1-y; x<1-x; x+(1-y)>y-x; 即x<1/2; y>1/2; y>x+1/2;
画图可以算得概率为1/8(线性规划思想).

4、一个面试题:快速生成10亿个不重复的18位随机数的算法(从n个数中生成m个不重复的随机数)
//假设从-n这n个数中生成m个不重复的数,且n小于int的表示范围
//总体思想是一开始每个数被选中的概率是m/n,于是随机一个数模n如果余数小于m则输出该数,同时m减
//否则继续扫描,以后的每个数被选中的概率都是m/(n-i)
void random_generate(int n, int m) { int i=1,t,remain; while(n-i>m) { t = rand()%(n-i); if(t<m){ printf("%d ",i); m--; } i++; } while(++i<=n)printf("%d ",i); }
(wiki关于随机数的介绍http://en.wikipedia.org/wiki/Mersenne_twister)
5、你有两个罐子以及50个红色弹球和50个蓝色弹球,随机选出一个罐子然后从里面随机选出一个弹球,怎么给出红色弹球最大的选中机会?在你的计划里,得到红球的几率是多少?
题目意思是两个罐子里面放了50红色和50蓝色弹球,然后我任选一个罐子,从中选中一个红球的最大概率,是设计一个两个罐子里怎么放这100球的计划。一个罐子:1个红球;另一个罐子:49个红球,50个篮球几率=1/2+(49/99)*(1/2)=74.7%。
6、一副扑克牌54张,现分成3等份每份18张,问大小王出现在同一份中的概率是多少?(大意如此)
解答1:
54张牌分成3等份,共有M=(C54取18)*(C36取18)*(C18取18)种分法。其中大小王在同一份的分法有N=(C3取1)*(C52取16)*(C36取18)*(C18取18)种。因此所求概率为P=N /M=17/53。
解答2:
不妨记三份为A、B、C份。大小王之一肯定在某一份中,不妨假定在A份中,概率为1/3。然后A份只有17张牌中可能含有另一张王,而B份、C份则各有18张牌可能含有另一张王,因此A份中含有另一张王的概率是17/(17+18+18)=17/53。也因此可知,A份中同时含有大小王的概率为1/3 * 17/53。题目问的是出现在同一份中的概率,因此所求概率为3*(1/3 * 17/53)=17/53。
7、A和B2人投硬币,正面A得1元,反面B得一元.起始时A有1元,B有100元. 游戏持续进行,直到其中1人破产才终止.
问:(出自投行面试题)
1.如果硬币正反概率相同,游戏的期待长度(expected duration)是几次投掷?
2.如果硬币是不公正的,正面概率为P,反面概率为Q.(P+Q=1), 那么游戏的期待长度(expectedduration)是几次投掷?
目前认为只有奇数次才可能破产。
第一问:1*0.5 + 3*0.5^3 + 5*0.5^5+。。。
以第二问为例,建立如下事件,即第N次出现恰好出现有人破产的概率为T(n),
那么问题的答案是计算E(T(n)),即该事件的期望值。
第1次出现破产的概率是p //只可能A破产
第2次出现 0 //因为A第1次赢了1个,共2个了,最多只能输1个,还会剩1个
第3次出现 q×p×p
第4次出现 0
第5次 q*q*p*p*p
第99次 q(49次方)×P(50次方)
--------------------------------------
在100次以下投掷次数时,不可能是B破产,只有可能是A破产
第100次时 只有B破产可能 即 q(100次方)
第101次 q(50次方)×P(51次方)
第102次 q(102次方)*p
综上所述,奇数次时,唯A可能破产,偶数次>=100时,唯 B可能破产。
E(T(n))=∑ n*T(n) n=1...+∞
=∑奇数次 +∑偶数次
=p/(1-p*q)+q(100次方)/(1-P*q)
其中q=1-p
问题1把p=q=1/2 代入即可。
8、2D平面上有一个三角形ABC,如何从这个三角形内部随机取一个点,且使得在三角形内部任何点被选取的概率相同。
在二维坐标系中可以用坐标(x,y)来表示图形中的一个点。如下图只要能够在各个带双向箭头的图之间的点能够建立一一映射即可。如把一个长方形(如正方形)的点映射到另一个长方形的点只要把坐标做相应的放大缩小即可。如把长方形的点映射到一个直角三角形,只要将长方形右上部份的三角形的点映射到对称的左下角的三角形的点即可。而直角三角形映射到一边平行于x轴的三角形的映射只要做x轴相应的偏移即可。而任意三角形可以分割成两个其中有一边平行于x轴的三角形。说的不是很清楚,具体的映射方法可以认真思考并写出公式。
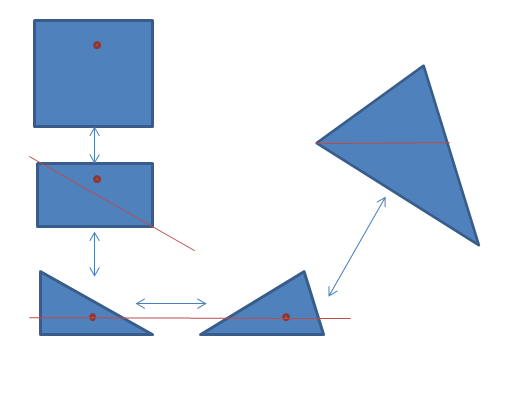
9、平均要取多少个(0,1)中的随机数才能让和超过1。答案: e 次, 其中e是自然对数的底

10、编程之美:金刚坐飞机问题
大家都在排队上飞机,然后金刚来了,他也有票,但是插队第一个上了飞机,随便找了个座位坐下了,其余人的策略是:
如果自己票上写的座位没被占就按照座位坐,被占了就变身成金刚,随便找地儿坐。问第i个人坐在自己座位的概率是多少?
1..n一共n个座位,为了方便计算起见,我们做一个变换
变换1:金刚的票上的座位是最后一个,也就是第n个,其余人的票和座位再按照原先的顺序排列成1..n-1。
这样并不影响最终的概率,因为如果
1)金刚坐在自己的位置上,那么大家同样都是肯定坐在自己的位置上。
2)如果金刚坐在第i个位置(非他票上的座位)上,那么前i-1个人会坐在自己的位置上,与变换前相同,而第i个人肯定不会坐在自己的位置上,他会在变换前的金刚的座位再加上i+1..n的集合中随机挑一个座位,这也有变换前相同,他挑的座位对于后面人的影响也是与变换前相同的。
设F(i,n)为新的n个座位的排列中第i个人坐到自己位置上的概率,那么旧排列中第i个人坐到自己位置的概率就是
F(i,n) i<j;
F(i-1,n) i>j;
j为金刚票上的座位
那么我们现在来计算F(i,n),后面的讨论全部基于变换后的排列。
对于乘客i,金刚的选择会造成3种情况,假设金刚选择的是j,分别为i<j,i=j,i>j,概率分别为(n-i)/n,1/n,(i-1)/n。
如果i<j,即金刚选择的座位在i的后面(我们做变换1的目的就在于此,如果不做那么还要考虑金刚坐到自己的位置的情况,而他自己的位置却是不确定的),那么乘客i必然会坐到自己的位置,概率为1,(n-i)/n*1
如果i=j,概率为0
如果i>j,那么前j-1个人肯定坐在自己的位置上,而第j个人就变身成了金刚,这样可以看做他就是金刚,他原来的座位就是n。
变换2:前j-1个人是打酱油的,跟后面的事件无关了,因为金刚在j上,所以第j个人变成了金刚2,他的票号是最后一个,j+1..n-1号乘客成了新的受害者,将j+1..n-1从1开始重新编号,座位数变成n-j
故第i个人坐在原来座位的概率为F(i-j,n-j)
所以概率为
综上
有
最后的结果是
F(i,n) i<j;
F(i-1,n) i>j;
j为金刚票上的座位




 浙公网安备 33010602011771号
浙公网安备 33010602011771号