腾讯笔试题
1、解释const的含义及实现机制
const的含义及实现机制,比如:const int i,是怎么做到i只可读的?
答:const用来说明所定义的变量是只读的。
这些在编译期间完成,编译器可能使用常数直接替换掉对此变量的引用。
2、买200返100优惠券,实际上折扣是多少?
到商店里买200的商品返还100优惠券(可以在本商店代替现金)。请问实际上折扣是多少?
答:由于优惠券可以代替现金,所以可以使用200元优惠券买东西,然后还可以获得100元的优惠券。
假设开始时花了x元,那么可以买到 x + x/2 + x/4 + ...的东西。所以实际上折扣是50%.(当然,大部分时候很难一直兑换下去,所以50%是折扣的上限)
如果使用优惠券买东西不能获得新的优惠券,那么
总过花去了200元,可以买到200+100元的商品,所以实际折扣为 200/300 = 67.7%.
3、简述tcp三次握手的过程,accept发生在三次握手哪个阶段?
要想明白Socket连接,先要明白TCP连接。设备能够使用联网功能是因为设备底层实现了TCP/IP协议,可以使设备终端通过无线网络建立TCP连接。TCP协议可以对上层网络提供接口,使上层网络数据的传输建立在“无差别”的网络之上。
建立起一个TCP连接需要经过“三次握手”:
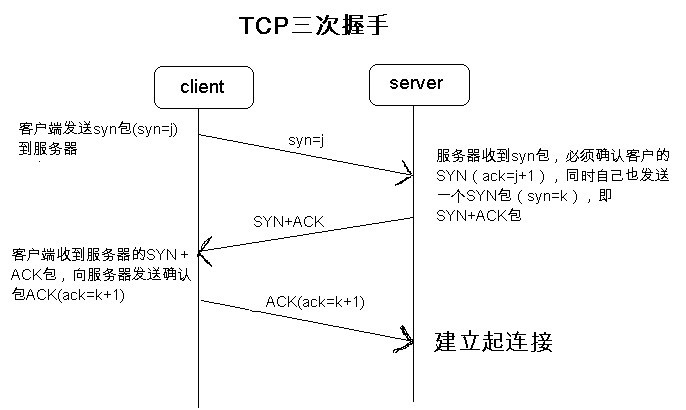
第一次握手:客户端发送syn包(syn=j)到服务器,并进入SYN_SEND状态,等待服务器确认;
第二次握手:服务器收到syn包,必须确认客户的SYN(ack=j+1),同时自己也发送一个SYN包(syn=k),即SYN+ACK包,此时服务器进入SYN_RECV状态;
第三次握手:客户端收到服务器的SYN+ACK包,向服务器发送确认包ACK(ack=k+1),此包发送完毕,客户端和服务器进入ESTABLISHED状态,完成三次握手。
三次握手完成后,客户端和服务器就建立了tcp连接。这时可以调用accept函数获得此连接。
握手过程中传送的包里不包含数据,三次握手完毕后,客户端与服务器才正式开始传送数据。理想状态下,TCP连接一旦建立,在通信双方中的任何一方主动关闭连接之前,TCP 连接都将被一直保持下去,如下图:
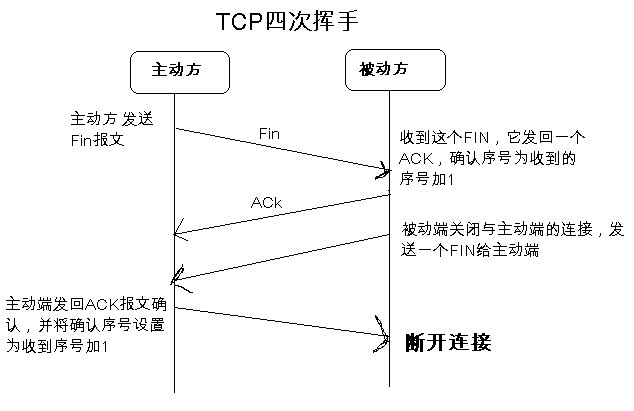
断开连接时服务器和客户端均可以主动发起断开TCP连接的请求,断开过程需要经过“四次挥手”(过程就不细写了,就是服务器和客户端交互,最终确定断开,如下图)
由于TCP连接是全双工的,因此每个方向都必须单独进行关闭。这个原则是当一方完成它的数据发送任务后就能发送一个FIN来终止这个方向 的连接。收到一个 FIN只意味着这一方向上没有数据流动,一个TCP连接在收到一个FIN后仍能发送数据。首先进行关闭的一方将执行主动关闭,而另一方执行被动关闭。
(1)主动端A发送一个FIN,用来关闭客户A到被动端B的数据传送。
(2)被动端B收到这个FIN,它发回一个ACK,确认序号为收到的序号加1。和SYN一样,一个FIN将占用一个序号。
(3)被动端B关闭与主动端A的连接,发送一个FIN给主动端A。
(4)主动端A发回ACK报文确认,并将确认序号设置为收到序号加1。
4、用UDP协议通讯时怎样得知目标机是否获得了数据包?
答:可以在每个数据包中插入一个唯一的ID,比如timestamp或者递增的int。发送方在发送数据时将此ID和发送时间记录在本地。接收方在收到数据后将ID再发给发送方作为回应发送方如果收到回应,则知道接收方已经收到相应的数据包;如果在指定时间内没有收到回应,则数据包可能丢失,需要重复上面的过程重新发送一次,直到确定对方收到。
5、求一个论坛的在线人数,假设有一个论坛,其注册ID有两亿个,每个ID从登陆到退出会向一个日志文件中记下登陆时间和退出时间,要求写一个算法统计一天中论坛的用户在线分布,取样粒度为秒。
答:一天总共有 3600*24 = 86400秒。
定义一个长度为86400的整数数组int delta[86400],每个整数对应这一秒的人数变化值,可能为正也可能为负。开始时将数组元素都初始化为0。
然后依次读入每个用户的登录时间和退出时间,将与登录时间对应的整数值加1,将与退出时间对应的整数值减1。
这样处理一遍后数组中存储了每秒中的人数变化情况。
定义另外一个长度为86400的整数数组int online_num[86400],每个整数对应这一秒的论坛在线人数。
假设一天开始时论坛在线人数为0,则第1秒的人数online_num[0] = delta[0]。第n+1秒的人数online_num[n] = online_num[n-1] + delta[n]。
这样我们就获得了一天中任意时间的在线人数。
6、在一个文件中有 10G 个整数,乱序排列,要求找出中位数。内存限制为 2G。
答:不妨假设10G个整数是64bit的。
2G内存可以存放256M个64bit整数。
我们可以将64bit的整数空间平均分成256M个取值范围,用2G的内存对每个取值范围内出现整数个数进行统计。这样遍历一边10G整数后,我们便知道中数在那个范围内出现,以及这个范围内总共出现了多少个整数。
如果中数所在范围出现的整数比较少,我们就可以对这个范围内的整数进行排序,找到中数。如果这个范围内出现的整数比较多,我们还可以采用同样的方法将此范围再次分成多个更小的范围(256M=2^28,所以最多需要3次就可以将此范围缩小到1,也就找到了中数)。
拿到此题目首先考虑的是内存的限制,因而无法用快速排序或是部分排序。若是求的是最大值或最小值,或是K小的值(k<2G)则可以采用堆排序O(NlogK)。但现在是求中位数即排在第5G和5G+1的数
算法思路分析:假设是无符号整数,
第一步: 借鉴桶排序的思路,因为整数为32位,我们先按高16位2^16=64K进行计数,即分成64K段,这样需要的计数数组大小为2^16,若数组类型为int型,存在缺点,若10G的数都是相同,这样数组存的计数最大为2^32=4G,就会出现溢出,所以数组类型采用long long8字节型。占用内存为2^16*8B=518KB。而内存给了2G,可见利用得过少,表明还有很大的改进空间。 改进:分成2G/8B=2^28=256M段,这样段越多,第二步扫描分析的数据就越少。
long long Counter[1 < <28];//256M桶 unsigned int x; memset(Counter,0,sizeof(Counter)); foreachnumber(x) { Counter[x>>4]++; //高28位 } long long sum=0; for(i=0;i <1 < <28;i++) { sum+=Counter[i]; if(sum>=5LL < <30)break;//找到中位数所在的段 } sum-=5LL < <30; sum=Counter[i]-sum;//为达到5G,中位数所在的段需要的个数 第二步:前步已把10G数据按高28位分到了256M桶中,且已经找到中位数在哪一段,只要把此段按低4位分到16个段中,即可以找到 int segment=i; memset(Counter,0,sizeof(Counter)); foreachnumber(x) { if((x>>16)==segment) { Counter[x&(~((-1) < <16))]++; //低4位。 -1的8位二进制表示为11111111 } } long long lsum=0; for(i=0;i <1 < <4;i++) { lsum+=Counter[i]; if(lsum>=sum)break; }
int keynum = (segment<<4)|(i);
总共只要读两遍整数,对每个整数也只是常数时间的操作,总体来说是线性时间
若是有符号的整数,只需改变映射即可
解法三:
关于中位数:数据排序后,位置在最中间的数值。即将数据分成两部分,一部分大于该数值,一部分小于该数值。中位数的位置:当样本数为奇数时,中位数=(N+1)/2 ; 当样本数为偶数时,中位数为N/2与1+N/2的均值(那么10G个数的中位数,就第5G大的数与第5G+1大的数的均值了)。
分析:明显是一道工程性很强的题目,和一般的查找中位数的题目有几点不同。
1. 原数据不能读进内存,不然可以用快速选择,如果数的范围合适的话还可以考虑桶排序或者计数排序,但这里假设是32位整数,仍有4G种取值,需要一个16G大小的数组来计数。
2. 若看成从N个数中找出第K大的数,如果K个数可以读进内存,可以利用最小或最大堆,但这里K=N/2,有5G个数,仍然不能读进内存。
3. 接上,对于N个数和K个数都不能一次读进内存的情况,《编程之美》里给出一个方案:设k<K,且k个数可以完全读进内存,那么先构建k个数的堆,先找出第0到k大的数,再扫描一遍数组找出第k+1到2k的数,再扫描直到找出第K个数。虽然每次时间大约是nlog(k),但需要扫描ceil(K/k)次,这里要扫描5次。
解法:首先假设是32位无符号整数。
1. 读一遍10G个整数,把整数映射到256M个区段中,用一个64位无符号整数给每个相应区段记数。
说明:整数范围是0 - 2^32 - 1,一共有4G种取值,映射到256M个区段,则每个区段有16(4G/256M = 16)种值,每16个值算一段, 0~15是第1段,16~31是第2段,……2^32-16 ~2^32-1是第256M段。一个64位无符号整数最大值是0~8G-1,这里先不考虑溢出的情况。总共占用内存256M×8B=2GB。
2. 从前到后对每一段的计数累加,当累加的和超过5G时停止,找出这个区段(即累加停止时达到的区段,也是中位数所在的区段)的数值范围,设为[a,a+15],同时记录累加到前一个区段的总数,设为m。然后,释放除这个区段占用的内存。
3. 再读一遍10G个整数,把在[a,a+15]内的每个值计数,即有16个计数。
4. 对新的计数依次累加,每次的和设为n,当m+n的值超过5G时停止,此时的这个计数所对应的数就是中位数。
总结:
1.以上方法只要读两遍整数,对每个整数也只是常数时间的操作,总体来说是线性时间。
2. 考虑其他情况。
若是有符号的整数,只需改变映射即可。若是64为整数,则增加每个区段的范围,那么在第二次读数时,要考虑更多的计数。若过某个计数溢出,那么可认定所在的区段或代表整数为所求,这里只需做好相应的处理。噢,忘了还要找第5G+1大的数了,相信有了以上的成果,找到这个数也不难了吧。
3. 时空权衡。
花费256个区段也许只是恰好配合2GB的内存(其实也不是,呵呵)。可以增大区段范围,减少区段数目,节省一些内存,虽然增加第二部分的对单个数值的计数,但第一部分对每个区段的计数加快了(总体改变??待测)。
4. 映射时尽量用位操作,由于每个区段的起点都是2的整数幂,映射起来也很方便。
7、两个整数集合A和B,求其交集。
答:(1) 读取整数集合A中的整数,将读到的整数插入到map中,并将对应的值设为1。
(2)读取整数集合B中的整数,如果该整数在map中并且值为1,则将此数加入到交集当中,并将在map中的对应值改为2。
通过更改map中的值,避免了将同样的值输出两次。
8、有1到10w这10w个数,去除2个并打乱次序,如何找出那两个数?
答:解法一:申请10w个bit的空间,每个bit代表一个数字是否出现过。
开始时将这10w个bit都初始化为0,表示所有数字都没有出现过。
然后依次读入已经打乱循序的数字,并将对应的bit设为1。
当处理完所有数字后,根据为0的bit得出没有出现的数字。
解法二:首先计算1到10w的和,平方和。
然后计算给定数字的和,平方和。
两次的到的数字相减,可以得到这两个数字的和,平方和。
所以我们有
x + y = n
x^2 + y^2 = m
解方程可以得到x和y的值。
9、有1000瓶水,其中有一瓶有毒,小白鼠只要尝一点带毒的水24小时后就会死亡,至少要多少只小白鼠才能在24小时时鉴别出那瓶水有毒?
答:最容易想到的就是用1000只小白鼠,每只喝一瓶。但显然这不是最好答案。
既然每只小白鼠喝一瓶不是最好答案,那就应该每只小白鼠喝多瓶。那每只应该喝多少瓶呢?
首先让我们换种问法,如果有x只小白鼠,那么24小时内可以从多少瓶水中找出那瓶有毒的?
由于每只小白鼠都只有死或者活这两种结果,所以x只小白鼠最大可以表示2^x种结果。如果让每种结果都对应到某瓶水有毒,那么也就可以从2^x瓶水中找到有毒的那瓶水。那如何来实现这种对应关系呢?
第一只小白鼠喝第1到2^(x-1)瓶,第二只小白鼠喝第1到第2^(x-2)和第2^(x-1)+1到第2^(x-1) + 2^(x-2)瓶....以此类推。
回到此题,总过1000瓶水,所以需要最少10只小白鼠。
10、给40亿个不重复的unsigned int的整数,没排过序的,然后再给几个数,如何快速判断这几个数是否在那40亿个数当中?
答:unsigned int 的取值范围是0到2^32-1。我们可以申请连续的2^32/8=512M的内存,用每一个bit对应一个unsigned int数字。首先将512M内存都初始化为0,然后每处理一个数字就将其对应的bit设置为1。当需要查询时,直接找到对应bit,看其值是0还是1即可。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号