二叉树的先序遍历

如下图表示一颗二叉树，对它进行先序遍历操作，采用两种方法，递归和非递归操作。。

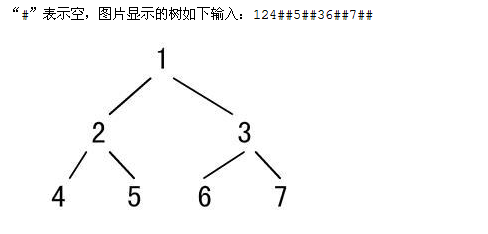
遍历结果为：1245367。

1、递归操作：

思想：若二叉树为空，返回。否则

1）遍历根节点；2）先序遍历左子树；3）先序遍历右子树

代码：

void PreOrder(BiTree root)  
{  
    if(root==NULL)  
        return ;  
    printf("%c ", root->data); //输出数据  
    PreOrder(root->lchild); //递归调用，先序遍历左子树  
    PreOrder(root->rchild); //递归调用，先序遍历右子树  
}  

2、非递归操作

思想：二叉树的非递归先序遍历，先序遍历思想：先让根进栈，只要栈不为空，就可以做弹出操作， 每次弹出一个结点，记得把它的左右结点都进栈，记得右子树先进栈，这样可以保证右子树在栈中总处于左子树的下面。

代码：

void PreOrder_Nonrecursive(BiTree T)     //先序遍历的非递归    
{  
    if(!T) return ;    
    stack<BiTree> s;  
    s.push(T);  
    while(!s.empty())  
    {  
        BiTree temp = s.top();  
        cout<<temp->data<<" ";  
        s.pop();  
        if(temp->rchild)  
            s.push(temp->rchild);  
        if(temp->lchild)  
            s.push(temp->lchild);  
    }  
}  

或者：

void PreOrder_Nonrecursive(BiTree T)     //先序遍历的非递归  
{  
    if(!T) return ;  
    stack<BiTree> s;  
    while(T)          // 左子树上的节点全部压入到栈中  
    {  
        s.push(T);  
        cout<<T->data<<"  ";  
        T = T->lchild;  
    }        
    while(!s.empty())  
    {          
        BiTree temp = s.top()->rchild;  // 栈顶元素的右子树  
        s.pop();                        // 弹出栈顶元素  
        while(temp)          // 栈顶元素存在右子树，则对右子树同样遍历到最下方  
        {  
            cout<<temp->data<<"  ";  
            s.push(temp);  
            temp = temp->lchild;  
        }  
    }  
}