二分搜索及其扩展
二分搜索
折半搜索,也称二分查找算法、二分搜索,是一种在有序数组中查找某一特定元素的搜索算法。搜素过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜素过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
时间复杂度:二分搜索每次把搜索区域减少一半,很明显时间复杂度为O(logN)。
空间复杂度:O(1),虽以递归形式定义,但是尾递归,可改写为循环。
二分搜索的基本实现
二分查找法在算法家族大类中属于“分治法”,分治法基本都可以用递归来实现的,二分查找法的递归实现如下:
int binary_search(int array[], int low, int high, int target) { if (low > high) return -1; int mid = (low + high)/2; if (array[mid]> target) return binary_search(array, low, mid -1, target); if (array[mid]< target) return binary_search(array, mid+1, high, target); return mid; }
非递归实现:
int binary_search(int arr[],int n ,int key){ int mid; int low = 0,high = n-1; while(low <= high){ mid = low + (high - low)/2; //中间元素,防止溢出 if(key == arr[mid]) return mid;//找到时返回 else if(key > arr[mid]){ low = mid + 1;//在更高的区间搜索 }else{ high = mid - 1;//在更低的区间搜索 } } return -1;//没有找到元素,返回-1 }
关于二分搜索,想起之前看过的一道题目:一个数组是由一个递减数列经过若干次左移形成的,例如{4,3,2,1,6,5}是由数组 {6,5,4,3,2,1}经过两次左移形成的,在这种数组中查找某一个数。函数原型是 int search(int a[],int low,int high,int k);
数组的形态如图所示:

仔细想想,如果取中间元素对数组进行划分的话,那么数组可以分为两个部分,数组的两个部分不外乎三种情况:
<a>有序 mid 有序
<b>部分有序 mid 有序
<c>有序 mid 部分有序
这样递归下去,用二分查找的一种变形,一样可以查找出。代码如下:
int bsearch(int a[], int n, int key) { int low = 0; int high = n-1; while(low <= high) { int mid = low + ((high - low) >> 1); if(a[mid] == key) return mid; if(a[mid] <= a[low]) {//左半段有序 if(key > a[mid] && key <= a[low]) { high = mid -1; } else { low = mid + 1; } } else { //右半段有序 if(key < a[mid] && key >= a[high]) { low = mid + 1; } else { high = mid -1; } } } return -1; }
搜狗还有一道面试题目:
有一个数组,该数组的特点是:前一部分递增有序,后一部分递减有序,求数组的峰值位置。
我们发现,给出的数组可能有如下三种形态:
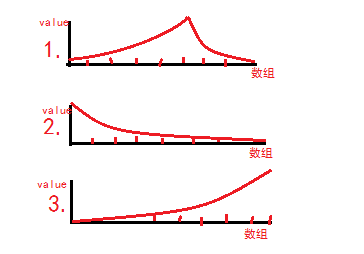
其中后两种情况是属于特殊的,是有序数组,峰值的位置就是数组的开始或结束索引。我们单单考虑第一种情况。
思考1:线性扫描,思路最简单,也最容易实现,只需扫描 一遍数组,比较当前元素与前一个元素的大小关系,一旦碰到当前元素比前一元素小,前一元素就是峰值。或者比较当前元素与后一元素,一旦后一元素比当前元素小,当前元素就是峰值。此方法的缺点是需要线性时间O(n)
思考2:考虑二分搜索,如果不考虑情况2和情况3.对于情况一而言,mid中间元素的位置不外乎三个情况:
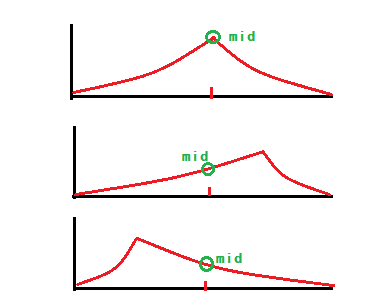
是不是跟二分搜索很类似?
我们可以根据中间元素与两边元素的大小关系,判断搜索左边还是右边。据此,不难写出如下代码(未经严格测试):
#include <stdio.h> //数组是先增后减数组。 int findMax(int *a ,int n){ int low = 0,high = n-1,mid; while(low <= high){ mid = low + ((high-low)>>1); if((mid + 1)<=high && (mid-1)>=low){ if(a[mid] >= a[mid-1] && a[mid] >= a[mid + 1]){ return mid; }else if(a[mid] >= a[mid-1] && a[mid] <=a[mid + 1]){ low = mid + 1; }else{ high = mid - 1; } }else if((mid+1) <= high){ if(a[mid] <= a[mid+1]){ return mid+1; }else{ return mid; } }else{ if(a[mid] <= a[mid-1]){ return mid-1; }else{ return mid; } } } } int main(){ int a[] = {1,2,7,6,5,4,3,1}; printf("%d \n",findMax(a,8)); }




