【学习笔记】折半搜索 Meet In The Middle
算法实现
我们正常的搜索应该是一个指数级的:\(2^n\)。
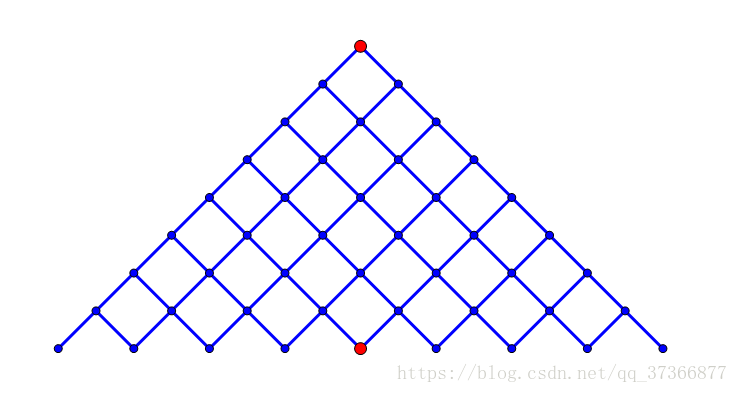
然而我们可以把这个搜索拆成两半,设小于整张图的限制 \(limit\) 为合法:
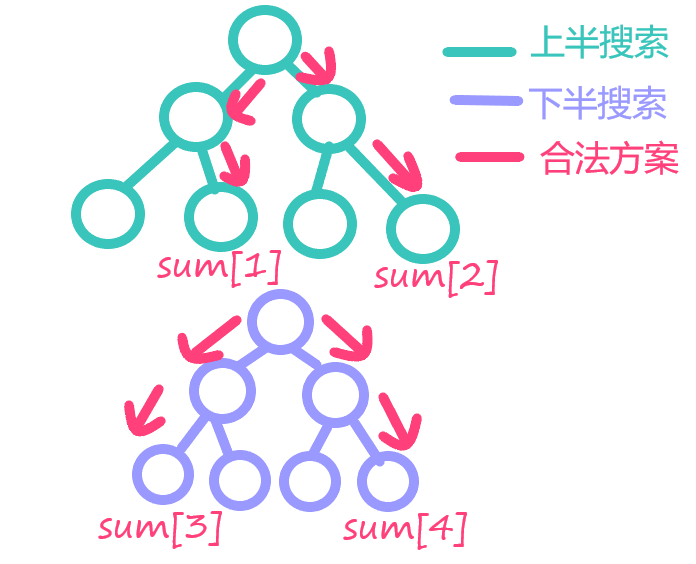
对于上半搜索,我们有若干符合限制的答案 \(sum_1\),对于下半搜索,我们有若干符合限制的答案 \(sum_2\)。
因此对于下半搜索,有一个匹配的限制:\(limit-sum_2[i],i\in sum_2\),在这个限制下,有多个上半搜索的匹配,类似于:

时间复杂度:\(O(2^{\frac{n}{2}+1})\),可能会带上查找的 \(+logn\)。
杂题乱写
[CEOI2015 Day2] 世界冰球锦标赛
折叠题干
[CEOI2015 Day2] 世界冰球锦标赛
题目描述
译自 CEOI2015 Day2 T1「Ice Hockey World Championship」
今年的世界冰球锦标赛在捷克举行。Bobek 已经抵达布拉格,他不是任何团队的粉丝,也没有时间观念。他只是单纯的想去看几场比赛。如果他有足够的钱,他会去看所有的比赛。不幸的是,他的财产十分有限,他决定把所有财产都用来买门票。
给出 Bobek 的预算和每场比赛的票价,试求:如果总票价不超过预算,他有多少种观赛方案。如果存在以其中一种方案观看某场比赛而另一种方案不观看,则认为这两种方案不同。
输入格式
第一行,两个正整数 \(N\) 和 \(M(1 \leq N \leq 40,1 \leq M \leq 10^{18})\),表示比赛的个数和 Bobek 那家徒四壁的财产。
第二行,\(N\) 个以空格分隔的正整数,均不超过 \(10^{16}\),代表每场比赛门票的价格。
输出格式
输出一行,表示方案的个数。由于 \(N\) 十分大,注意:答案 \(\le 2^{40}\)。
样例 #1
样例输入 #1
5 1000
100 1500 500 500 1000
样例输出 #1
8
提示
样例解释
八种方案分别是:
- 一场都不看,溜了溜了
- 价格 \(100\) 的比赛
- 第一场价格 \(500\) 的比赛
- 第二场价格 \(500\) 的比赛
- 价格 \(100\) 的比赛和第一场价格 \(500\) 的比赛
- 价格 \(100\) 的比赛和第二场价格 \(500\) 的比赛
- 两场价格 \(500\) 的比赛
- 价格 \(1000\) 的比赛
有十组数据,每通过一组数据你可以获得 10 分。各组数据的数据范围如下表所示:
| 数据组号 | \(1-2\) | \(3-4\) | \(5-7\) | \(8-10\) |
|---|---|---|---|---|
| \(N \leq\) | \(10\) | \(20\) | \(40\) | \(40\) |
| \(M \leq\) | \(10^6\) | \(10^{18}\) | \(10^6\) | \(10^{18}\) |
这不板子题(
Miku's Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
#define MYMAX 20070831
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
int Max(int x,int y)<%if(x<y) return y;return x;%>
int Min(int x,int y)<%if(x<y) return x;return y;%>
int Abs(int x)<%if(x<0) return x*(-1);return x;%>
#if ONLINE_JUDGE
char in[1<<20],*p1=in,*p2=in;
#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#endif
inline ll read(){
char c=getchar();
ll x=0,f=1;
while(c<48)<%if(c=='-')f=-1;c=getchar();%>
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}const int maxn=45;
int n;
ll m,cost[maxn];
vector<ll> s1,s2;
void dfs(int st,int to,ll sum,vector<ll>&now){
if(sum>m) return;
if(st>to){
now.push_back(sum);
return;
}
dfs(st+1,to,sum+cost[st],now);
dfs(st+1,to,sum,now);
}
int main(){
n=read(),m=read();
for(rg i=1;i<=n;++i) cost[i]=read();
dfs(1,n/2,0,s1);
dfs(n/2+1,n,0,s2);
sort(s1.begin(),s1.end());
ll ans=0;
int len2=s2.size()-1;
for(rg i=0;i<=len2;++i) ans+=upper_bound(s1.begin(),s1.end(),m-s2[i])-s1.begin();
printf("%lld\n",ans);
}
2023年多校联训NOIP层测试2 T2 期末考试
折叠题干
Problem B. 期末考试
Input file: standard input
Output file: standard output
Time limit: 1 second
Memory limit: 1024 megabytes
小X和小Y正在进行期末考试!
期末考试的试卷上共有10道选择题,每道题从ABCD中选择一个正确选项,选对得10分,选错得0分。 由于小Y上课时从来没有认真听讲,他只能每道题都从ABCD四个选项中等概率随机选择一个。正当 他焦头烂额之时,他看到了坐在他旁边的小X。聪明的小X自然会做每一道题目,但他不愿意直接告诉 小Y每道题的答案,而是让小Y把自己的答案传给小X,小X为小Y评分。 现在小Y已经将n 种答案交给了小X,小X也为其一一打分,但小Y还是不知道正确答案是什么,现在, 小Y想请你算算有多少种可能的正确答案?
Input
第一行输入一个T,表示数据组数。 接下来对于每组数据,首先输入一个n,表示小Y的答题次数。 接下来n 行,每行一个长度为10的字符串和一个数字a,表示小Y的答案和得分。
Output
输出T行,每行一个整数表示有多少种可能的正确答案。
Sample Input 1
3
3
AAAAAAAAAA 0
BBBBBBBBBB 0
CCCCCCCCCC 0
1
CCCCCCCCCC 90
2
AAAAAAAAAA 10
ABCDABCDAB 20
Sample Output 1
1
30
57456
Note
对于第一组数据,由于ABC都不可能是答案,答案为DDDDDDDDDD。 对于30%数据,T = 1, n ≤ 10。 对于另10%数据,a = 0。 对于另10%数据,a = 90。 对于100%数据,1 ≤ T ≤ 20000,1 ≤ n ≤ 20000,0 ≤ a ≤ 100,所有的a都是10的倍数。所有数据中 的n的和≤ 20000。
首先要知道这道题的暴力做法,纯搜索。
BF
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
#define MYMAX 20070831
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
int Max(int x,int y)<%if(x<y) return y;return x;%>
int Min(int x,int y)<%if(x<y) return x;return y;%>
int Abs(int x)<%if(x<0) return x*(-1);return x;%>
//#if ONLINE_JUDGE
//char in[1<<20],*p1=in,*p2=in;
//#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
//#endif
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48)<%if(c=='-')f=-1;c=getchar();%>
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}const int maxn=20050;
int T,n,ans,a[maxn];
char s[maxn][11],tryy[10];
void dfs(int pos,int n){
int pts=0;
if(pos==11){
for(rg i=1;i<=n;++i){
pts=0;
for(rg j=1;j<=10;++j){
if(tryy[j]==s[i][j]) pts+=10;
}
if(pts!=a[i]) return;
}
++ans;
}
else{
for(rg i=1;i<=4;++i){
tryy[pos]='A'-1+i;
dfs(pos+1,n);
}
}
}
int main(){
T=read();
while(T--){
ans=0;
n=read();
for(rg i=1;i<=n;++i){
scanf("%s",s[i]+1);
a[i]=read();
}
dfs(1,n);
printf("%d\n",ans);
}
return 0;
}
然后看到长度为 \(10\),考虑折半搜索,这是好的。
前五个字母在 \(n\) 个字符串的得分情况+后五个字符在 \(n\) 个字符串的得分情况=\(n\) 个字符串的得分情况。
\(n\) 个字符串的得分情况-后五个字符在 \(n\) 个字符串的得分情况=前五个字符在 \(n\) 个字符串的得分情况。
所以我们可以把等号前面的得分情况看作一个字符串,求哈希然后放容器里,等号后面的得分情况看作一个字符串,求哈希放桶里,最后查询一下等号前面的哈希在桶里出现了多少次即可。
Miku's Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
#define MYMAX 20070831
#define int long long
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
int Max(int x,int y)<%if(x<y) return y;return x;%>
int Min(int x,int y)<%if(x<y) return x;return y;%>
int Abs(int x)<%if(x<0) return x*(-1);return x;%>
//#if ONLINE_JUDGE
//char in[1<<20],*p1=in,*p2=in;
//#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
//#endif
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48)<%if(c=='-')f=-1;c=getchar();%>
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}const int maxn=20050,p=131,mod=19491001;
int T,n,ans,a[maxn];
char s[maxn][11],tryy[11];
vector<int> need;
map<int,int> bucket;
il void clear(){
need.clear();
bucket.clear();
ans=0;
}
void dfs1(int st,int pos,int to,map<int,int>&now){
//将前五个变哈希
int pts=0;
if(pos==to+1){
int has=0;
for(rg i=1;i<=n;++i){
pts=0;
for(rg j=st;j<=to;++j){
if(tryy[j]==s[i][j]) pts+=10;
}
if(a[i]-pts<0 || a[i]-pts>50) return;
has=(has*p+pts)%mod;
}
++now[has];
}
else{
for(rg i=1;i<=4;++i){
tryy[pos]='A'-1+i;
dfs1(st,pos+1,to,now);
}
}
}
void dfs2(int st,int pos,int to,vector<int>&now){
//针对后五个,得到需要的,变哈希
int pts=0;
if(pos==to+1){
int has=0;
for(rg i=1;i<=n;++i){
pts=0;
for(rg j=st;j<=to;++j){
if(tryy[j]==s[i][j]) pts+=10;
}
if(a[i]-pts<0 || a[i]-pts>50) return;
// for(rg j=st;j<=to;++j) cout<<tryy[j];
// cout<<endl;
has=(has*p+a[i]-pts)%mod;
}
now.push_back(has);
}
else{
for(rg i=1;i<=4;++i){
tryy[pos]='A'-1+i;
dfs2(st,pos+1,to,now);
}
}
}
signed main(){
T=read();
while(T--){
ans=0;
n=read();
for(rg i=1;i<=n;++i){
scanf("%s",s[i]+1);
a[i]=read();
}
dfs1(1,1,5,bucket);
dfs2(6,6,10,need);
int len=need.size()-1;
for(rg i=0;i<=len;++i)<% ans+=bucket[need[i]]; %>
printf("%d\n",ans);
clear();
}
return 0;
}
/*
1
10
DABBABBDDB 20
BABABDBBCB 30
CBCCDABCCC 20
CCDADDADAC 20
CBCDBAABCB 30
DADABBBCCB 20
ACBCADCBBD 30
DDDACDDBDA 20
DDBDBBDBCB 20
DCDCBDACCB 20
*/

