园龄：2年粉丝：80 关注：96

【学习笔记】【数学】计算几何基础

点击查看目录

前置知识：
叉积与跨立实验
例题：
- [SCOI2007] 折纸
  - 解题：

前置知识：

建议虽然是简单的前置知识，还是打开略过一遍。

浮点数与误差分析（少用除法）
向量相关

向量

向量，就是带有方向和大小两个属性的边，通常形式为 $\overrightarrow{AB}=(a_1，a_2)=A$ 。

运算与性质：

判等：两点坐标重合。

 il int dcmp(double a){
    if(a<-eps)	return -1;
    if(a>eps)	return 1;
    return 0;
}
il bool operator==(node a,node b)<% return !dcmp(a.x-b.x) && !dcmp(a.y-b.y); %>

加减： $A+B=(a_1,a_2)+(b_1,b_2)=(a_1+b_1,a_2+b_2)$ 。

 il node operator+(node a,node b)<% return node(a.x+b.x,a.y+b.y); %>
il node operator-(node a,node b)<% return node(a.x-b.x,a.y-b.y); %>

模长： $|A|=\sqrt{a_1^2+a_2^2}$ 。

 il double len(node a)<% return sqrt(dot(a,a)); %>
//dot是点乘函数

角度： $\tan \theta =\frac{a_2}{a_1},\theta =arctan \frac{a_2}{a_1}$
数乘： $k\times A=k\times (a_1,a_2)=(ka_1,ka_2)$ 。

 il node operator*(node a,double k)<% return node(a.x*k,a.y*k); %>

点乘： $A\cdot B=(a_1,a_2)\cdot (b_1,b_2)=a_1b_1+a_2b_2$ 。

（几何意义： $A$ 乘上 $B$ 在 $A$ 上的投影，即 $|A|\times |B|\times cos \Theta$ )

 il double dot(node a,node b)<% return a.x*b.x+a.y*b.y; %>

夹角： $\cos \theta=\frac{A\cdot B}{|A|\times |B|}$ 。

 il double angle(node a,node b)<% return acos(dot(a,b)/len(a)/len(b)); %>

若 $A\cdot B=0$ ，（ $A,B$ 不为0）则 $A$ 与 $B$ 垂直， $>0$ 为锐角， $<0$ 为钝角。
叉积： $A\times B=\begin{vmatrix} a_1&b_1\\a_2&b_2 \end{vmatrix}=a_1b_2-b_1a_2=-B\times A$ 。

（几何意义：叉积的绝对值=面积）

 il double cro(node a,node b)<% return a.x*b.y-a.y*b.x; %>

面积： $|A\times B|=|A||B|\sin \theta$ 。
旋转：将 $A$ 旋转 $\alpha$ 弧度得到 $A'$ ：

$A=(a_1,a_2)=r(\cos\theta,\sin\theta);$

$A'=r(\cos(\theta+\alpha),\sin(\theta+\alpha)=r(\cos\theta \cos\alpha-\sin\theta \sin\alpha,\cos\theta \sin\alpha+sin\theta \cos\alpha)$

$=(a_1 \cos\alpha-a_2 \sin\alpha,a_1 \sin\alpha+a_2 \cos\alpha)$

直线与线段相关

直线与线段

直线一般形式有四：

\begin{aligned} a x + b y + c = 0 \\ y = k x + b \\ 两 个 端 点 \\ 一 个 起 点 和 一 个 向 量 \end{aligned}

$\begin{aligned} &ax+by+c=0\\ &y=kx+b\\ &两个端点\\ &一个起点和一个向量 \end{aligned}$

其中， $k$ 是直线的斜率， $k=\frac{y_2-y_1}{x_2-x_1}=tan \alpha$ ， $b$ 是直线的截距。

特别地，当两条直线垂直时有 $k1\times k2=-1$ 。

而线段，在代码中往往可以这样表示：

 struct Node{double x,y;};
struct line{node p1,p2;};

有以下运算：

判断点 $P$ 是否在直线 $AB$ 上。

 il int judge_LINE(Node p,Node a,Node b)<% return !mystd::dcmp(Vector::cro(p-a,b-a)); %>

判断点 $P$ 是否在线段 $AB$ 上。

 il int judge_line(Node p,Node a,Node b)<% return !mystd::dcmp(cro(p-a,b-a)) && mystd::dcmp(mystd::fMin(a.x,b.x)-p.x)<=0 && mystd::dcmp(p.y-mystd::fMax(a.y,b.y))<=0 && mystd::dcmp(p.x-mystd::fMax(a.x,b.x))<=0 && mystd::dcmp(mystd::fMin(a.y,b.y)-p.y)<=0; %>

求点 $P$ 到直线 $AB$ 的垂足。

 il Node footnode(Node p,Node a,Node b){
		Node x=p-a,y=p-b,z=b-a;
		double len1=Vector::dot(x,z)/Vector::len(z),len2=-1.0*Vector::dot(y,z)/Vector::len(z);
		return a+z*(len1/(len1+len2));
	}

证明：见图。

求点 $P$ 到直线 $AB$ 的对称点：

 il Node symmetry(Node p,Node a,Node b)<% return p+(footnode(p,a,b)-p)*2; %>

求直线 $AB$ 与直线 $CD$ 的交点：

 il Node internode(Node a,Node b,Node c,Node d)<% Node x=b-a,y=d-c,z=a-c;return a+x*(Vector::cro(y,z)/Vector::cro(x,y)); %>

证明：相似，见图。

判断直线 $AB$ 与线段 $CD$ 是否相交：

 il int judge_CROSS(Node a,Node b,Node c,Node d)<% return judge_line(internode(a,b,c,d),c,d); %>

看交点是否在线段 $CD$ 即可。

判断线段 $AB$ 与线段 $CD$ 是否相交：

 il int judge_cross(Node a,Node b,Node c,Node d){
		double c1=cro(b-a,c-a),c2=cro(b-a,d-a);
		double d1=cro(d-c,a-c),d2=cro(d-c,b-c);
		return mystd::dcmp(c1)*mystd::dcmp(c2)<0 && mystd::dcmp(d1)*mystd::dcmp(d2)<0;
	}

看端点是否在两侧即可，根据下面的跨立实验得。

判断一点是否在一任意多边形内：

 il int PIP(Node *P,int n,Node a){
		int cnt=0,j;
		double res=0.0;
		for(rg i=1;i<=n;++i){
			if(i<n)	j=i+1;
			else	j=1;
			if(judge_line(a,P[i],P[j]))	return 2;//点在多边形上
			if(a.y>=mystd::fMin(P[i].y,P[j].y) && a.y<mystd::fMax(P[i].y,P[j].y)){
			//纵坐标在该线段两端点之间 
				res=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x);
				//res是同一纵坐标下的在该边上的点的横坐标 
				cnt=cnt+(mystd::dcmp(res-a.x)>0);
			} 
		}
		return cnt&1;		//奇数次就是在多边形内 
	}

证明见注释。

因此有缺省源：

缺省源

 #include<bits/stdc++.h>
using namespace std;
#define rg register int
#define il inline
typedef long long ll;
typedef long double llf;
const double eps=1e-8; 
namespace mystd{
	il int Max(int a,int b)<%if(a<b) return b;return a; %>
	il int Min(int a,int b)<%if(a>b) return b;return a; %>
	il int Abs(int a)<% if(a<0) return a*(-1);return a; %>
	il double fMax(double a,double b)<%if(a<b) return b;return a; %>
	il double fMin(double a,double b)<%if(a>b) return b;return a; %>
	il double fAbs(double a)<% if(a<0) return a*(-1);return a; %>
	il int dcmp(double a){
		if(a<-eps)	return -1;
		if(a>eps)	return 1;
		return 0;
	}
}
struct Node<% double x,y; Node(double xx=0,double yy=0)<% x=xx,y=yy; %> %>;
il bool operator==(Node a,Node b)<% return !mystd::dcmp(a.x-b.x) && !mystd::dcmp(a.y-b.y); %>
il Node operator+(Node a,Node b)<% return Node(a.x+b.x,a.y+b.y); %>
il Node operator-(Node a,Node b)<% return Node(a.x-b.x,a.y-b.y); %> 
il Node operator*(Node a,double k)<% return Node(a.x*k,a.y*k); %>
namespace Vector{
	il double dot(Node a,Node b)<% return a.x*b.x+a.y*b.y; %>				//点乘 	
	il double len(Node a)<% return sqrt(dot(a,a)); %>						//模长
	il double angle(Node a,Node b)<% return acos(dot(a,b)/len(a)/len(b)); %>//夹角 
	il double cro(Node a,Node b)<% return a.x*b.y-a.y*b.x; %>				//叉积 
	il int judge_LINE(Node p,Node a,Node b)<% return !mystd::dcmp(cro(p-a,b-a)); %>
	//判断p是否在直线AB上
	il int judge_line(Node p,Node a,Node b)<% return !mystd::dcmp(cro(p-a,b-a)) && mystd::dcmp(mystd::fMin(a.x,b.x)-p.x)<=0 && mystd::dcmp(p.y-mystd::fMax(a.y,b.y))<=0 && mystd::dcmp(p.x-mystd::fMax(a.x,b.x))<=0 && mystd::dcmp(mystd::fMin(a.y,b.y)-p.y)<=0; %>
	//判断p是否在线段AB上 
	il Node footnode(Node p,Node a,Node b){
		Node x=p-a,y=p-b,z=b-a;
		double len1=dot(x,z)/len(z),len2=-1.0*dot(y,z)/len(z);
		return a+z*(len1/(len1+len2));
	}
	//求p到直线AB的垂足
	il Node symmetry(Node p,Node a,Node b)<% return p+(footnode(p,a,b)-p)*2; %>
	//求p到直线AB的对称点
	il Node internode(Node a,Node b,Node c,Node d)<% Node x=b-a,y=d-c,z=a-c;return a+x*(cro(y,z)/cro(x,y)); %>
	//直线AB与CD交点 
	il int judge_CROSS(Node a,Node b,Node c,Node d)<% return judge_line(internode(a,b,c,d),c,d); %>
	//判断直线AB与线段CD是否有交点 
	il int judge_cross(Node a,Node b,Node c,Node d){
		double c1=cro(b-a,c-a),c2=cro(b-a,d-a);
		double d1=cro(d-c,a-c),d2=cro(d-c,b-c);
		return mystd::dcmp(c1)*mystd::dcmp(c2)<0 && mystd::dcmp(d1)*mystd::dcmp(d2)<0;
	}
	//判断线段AB与线段CD是否有交点 
	il int PIP(Node *P,int n,Node a){
		int cnt=0,j;
		double res=0.0;
		for(rg i=1;i<=n;++i){
			if(i<n)	j=i+1;
			else	j=1;
			if(judge_line(a,P[i],P[j]))	return 2;//点在多边形上
			if(a.y>=mystd::fMin(P[i].y,P[j].y) && a.y<mystd::fMax(P[i].y,P[j].y)){
			//纵坐标在该线段两端点之间 
				res=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x);
				//res是同一纵坐标下的在该边上的点的横坐标 
				cnt=cnt+(mystd::dcmp(res-a.x)>0);
			} 
		}
		return cnt&1;		//奇数次就是在多边形内 
	}
	//判断点a是否在多边形P内部 
}

叉积与跨立实验

我们在前置知识中已经提到叉积，但是叉积的什么“右手定则”我不会，长大再学（

上面提到，对于向量 $A(x_1,y_1),B(x_2,y_2)$ ，有叉积： $x_1y_2-x_2y_1$ 。

（下有证明，别急）

以 $p_0$ 为参考点，有代码：

叉积

 double multi(node p1, node p2, node p0) {
    double x1, y1, x2, y2;
    x1 = p1.x - p0.x;
    y1 = p1.y - p0.y;
    x2 = p2.x - p0.x;
    y2 = p2.y - p0.y;
    return x1 * y2 - x2 * y1;
}

而该函数返回值若大于 $0$ ，证明 $p_2$ 在 $p_1$ 逆时针方向，小于 $0$ 则在顺时针方向，若等于 $0$ 则共线。

为什么？我们现在来证明这个公式。

\begin{aligned} x_{1} y_{2} - x_{2} y_{1} \\ = (| A | \cos θ_{1}) (| B | \sin θ_{2}) - (| A | \sin θ_{1}) (| B | \cos θ_{2}) \\ = | A | | B | \cos θ_{1} \sin θ_{2} - | A | | B | \sin θ_{1} \cos θ_{2} \\ = | A | | B | \sin (θ_{2} - θ_{1}) \\ = - | A | | B | \sin θ \end{aligned}

$\begin{aligned} x_1y_2-x_2y_1\\ &=(|A|\cos\theta_1)(|B|\sin\theta_2)-(|A|\sin\theta_1)(|B|\cos\theta_2)\\ &=|A||B|\cos\theta_1\sin\theta_2-|A||B|\sin\theta_1\cos\theta_2\\ &=|A||B|\sin(\theta_2-\theta_1)\\ &=-|A||B|\sin\theta \end{aligned}$

所以，当 $x_1y_2-x_2y_1>0$ ，意味着 $\sin\theta<0$ ，就是 $B$ 在 $A$ 的逆时针方向。

例题：

[SCOI2007] 折纸

[SCOI2007] 折纸

题目链接

题目描述

桌上有一张边界平行于坐标轴的正方形纸片，左下角的坐标为(0,0)，右上角的坐标为(100,100)。接下来执行n条折纸命令。每条命令用两个不同点P1(x1,y1)和P2(x2,y2)来表示，执行时把当前的折纸作品沿着P1P2所在直线折叠，并把有向线段P1P2的右边折向左边（左边的部分保持不变）。

折叠结束后，需要在作品上打一个孔，然后用绳子穿起来挂在墙上。孔的位置是相当重要的：若需要穿过太多层的纸，打孔本身比较困难；若穿过的层数太少，悬挂起来以后作品可能会被撕破。为了选择一个比较合适的打孔位置，你需要计算在每个候选位置打孔时穿过的层数。如果恰好穿过某一层的边界（误差0.000001内），则该层不统计在结果中。

本题考虑一个简化的模型：纸的厚度不计，因此折纸操作总能完美执行。

输入格式

输入第一行为一个整数n，即折纸的次数。以下n行每行四个实数x1,y1,x2,y2，表示每次折纸时对应的有向线段。

下一行包含一个正整数m，即候选位置的个数，以下每行包含两个实数x,y，表示一个候选位置。

输出格式

每个候选位置输出一行，包含一个整数，即该位置打孔时穿过的层数。

样例 #1

样例输入 #1

 2
-0.5 -0.5 1 1
1 75 0 75
6
10 60
80 60
30 40
10 10
50 50
20 50

样例输出 #1

提示

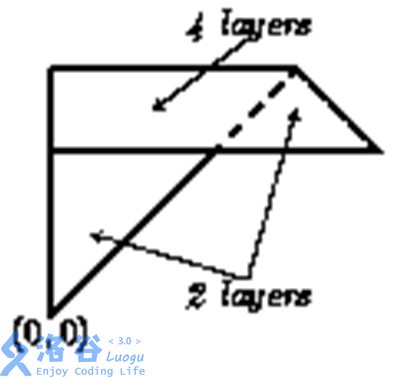
20%的数据满足：n<=1

100%的数据满足：0<=n<=8, 1<=m<=50

解题：

这个题数据范围 $0\leq n\leq 8$ 非常的小，可以暴力。

折叠嘛，给出来一条线，分类讨论：

把线右边的折到左边，用到上面的跨立实验和求对称点。
线上的不用动。
如果不在右边也不在线上就更不用动了。

我们开两个点结构体，分别是 $R$ 和 $L$ ，表示原本在线右边的点折叠后位置，原本在线左边的点折叠后位置。

第一种情况是将对称点进入 $R$ 。

第二种情况是将线上点进入 $L$ 与 $R$ 。

第三种情况是将左边原点进入 $L$ 。

我们最开始的顶点是很容易得到的，一个正方形嘛。

因此先将顶点进行这样的操作，之后，我们要考虑这个边与线的交点，入 $L,R$ 。

但是呢，因为可能是三边交点相同，所以要去重。

得到一堆新的多边形，作为新的图形重复操作。

最后对于一个点暴力枚举所有多边形是否包含它。

Miku's Code

 #include<bits/stdc++.h>
using namespace std;
#define rg register int
#define il inline
typedef long long ll;
typedef long double llf;
const double eps=1e-8; 
namespace mystd{
	il int Max(int a,int b)<%if(a<b) return b;return a; %>
	il int Min(int a,int b)<%if(a>b) return b;return a; %>
	il int Abs(int a)<% if(a<0) return a*(-1);return a; %>
	il double fMax(double a,double b)<%if(a<b) return b;return a; %>
	il double fMin(double a,double b)<%if(a>b) return b;return a; %>
	il double fAbs(double a)<% if(a<0) return a*(-1);return a; %>
	il int dcmp(double a){
		if(a<-eps)	return -1;
		if(a>eps)	return 1;
		return 0;
	}
}
struct Node<% double x,y; Node(double xx=0,double yy=0)<% x=xx,y=yy; %> %>;
il bool operator==(Node a,Node b)<% return !mystd::dcmp(a.x-b.x) && !mystd::dcmp(a.y-b.y); %>
il Node operator+(Node a,Node b)<% return Node(a.x+b.x,a.y+b.y); %>
il Node operator-(Node a,Node b)<% return Node(a.x-b.x,a.y-b.y); %> 
il Node operator*(Node a,double k)<% return Node(a.x*k,a.y*k); %>
namespace Vector{
	il double dot(Node a,Node b)<% return a.x*b.x+a.y*b.y; %>				//点乘 	
	il double len(Node a)<% return sqrt(dot(a,a)); %>						//模长
	il double angle(Node a,Node b)<% return acos(dot(a,b)/len(a)/len(b)); %>//夹角 
	il double cro(Node a,Node b)<% return a.x*b.y-a.y*b.x; %>				//叉积 
	il int judge_LINE(Node p,Node a,Node b)<% return !mystd::dcmp(cro(p-a,b-a)); %>
	//判断p是否在直线AB上
	il int judge_line(Node p,Node a,Node b)<% return !mystd::dcmp(cro(p-a,b-a)) && mystd::dcmp(mystd::fMin(a.x,b.x)-p.x)<=0 && mystd::dcmp(p.y-mystd::fMax(a.y,b.y))<=0 && mystd::dcmp(p.x-mystd::fMax(a.x,b.x))<=0 && mystd::dcmp(mystd::fMin(a.y,b.y)-p.y)<=0; %>
	//判断p是否在线段AB上 
	il Node footnode(Node p,Node a,Node b){
		Node x=p-a,y=p-b,z=b-a;
		double len1=dot(x,z)/len(z),len2=-1.0*dot(y,z)/len(z);
		return a+z*(len1/(len1+len2));
	}
	//求p到直线AB的垂足
	il Node symmetry(Node p,Node a,Node b)<% return p+(footnode(p,a,b)-p)*2; %>
	//求p到直线AB的对称点
	il Node internode(Node a,Node b,Node c,Node d)<% Node x=b-a,y=d-c,z=a-c;return a+x*(cro(y,z)/cro(x,y)); %>
	//直线AB与CD交点 
	il int judge_CROSS(Node a,Node b,Node c,Node d)<% return judge_line(internode(a,b,c,d),c,d); %>
	//判断直线AB与线段CD是否有交点 
	il int judge_cross(Node a,Node b,Node c,Node d){
		double c1=cro(b-a,c-a),c2=cro(b-a,d-a);
		double d1=cro(d-c,a-c),d2=cro(d-c,b-c);
		return mystd::dcmp(c1)*mystd::dcmp(c2)<0 && mystd::dcmp(d1)*mystd::dcmp(d2)<0;
	}
	//判断线段AB与线段CD是否有交点 
	il int PIP(Node *P,int n,Node a){
		int cnt=0,j;
		double res=0.0;
		for(rg i=1;i<=n;++i){
			if(i<n)	j=i+1;
			else	j=1;
			if(judge_line(a,P[i],P[j]))	return 2;//点在多边形上
			if(a.y>=mystd::fMin(P[i].y,P[j].y) && a.y<mystd::fMax(P[i].y,P[j].y)){
			//纵坐标在该线段两端点之间 
				res=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x);
				//res是同一纵坐标下的在该边上的点的横坐标 
				cnt=cnt+(mystd::dcmp(res-a.x)>0);
			} 
		}
		return cnt&1;		//奇数次就是在多边形内 
	}
	//判断点a是否在多边形P内部 
}
const int maxn=8;
 
Node a,b;
struct ewq{
	int ncnt;
	Node node[maxn*maxn+5];
};ewq py[(1<<maxn)+5],qy[(1<<maxn)+5];
int T,n,t,tt;
 
il bool judge(Node a,Node l,Node r){
//判断AL是否在AR的顺时针方向即右边 
	return mystd::dcmp(Vector::cro(l-a,r-a))>0;
}
 
il void cut(ewq e,Node a,Node b){
	ewq L,R;
	L.ncnt=R.ncnt=0;
	for(rg i=1;i<=e.ncnt;++i){
		if(judge(a,e.node[i],b))	R.node[++R.ncnt]=Vector::symmetry(e.node[i],a,b);		//在右边就折叠 
		else if(Vector::judge_LINE(e.node[i],a,b))	L.node[++L.ncnt]=R.node[++R.ncnt]=e.node[i];
		else	L.node[++L.ncnt]=e.node[i];
		rg j;
		if(i<e.ncnt)	j=i+1;
		else	j=1;
		if(Vector::judge_CROSS(a,b,e.node[i],e.node[j])){
			//如果直线AB与线段node[i]-node[i+1]有交点,交点进入
			L.node[++L.ncnt]=R.node[++R.ncnt]=Vector::internode(a,b,e.node[i],e.node[j]);
		}
		while(L.ncnt>1 && L.node[L.ncnt]==L.node[L.ncnt-1])	--L.ncnt;
		while(R.ncnt>1 && R.node[R.ncnt]==R.node[R.ncnt-1])	--R.ncnt;
		//去重
	}
	if(L.ncnt>1 && L.node[1]==L.node[L.ncnt]) --L.ncnt;
	if(R.ncnt>1 && R.node[1]==R.node[R.ncnt]) --R.ncnt;
	if(L.ncnt)	qy[++tt]=L;
	if(R.ncnt)	qy[++tt]=R;
} 
 
il void pre(){
//初始化100*100正方形 
	py[++t].ncnt=4;
	py[t].node[1]=Node<% 0,0 %>;
	py[t].node[2]=Node<% 0,100 %>;
	py[t].node[3]=Node<% 100,100 %>;
	py[t].node[4]=Node<% 100,0 %>; 
}
 
int main(){
#ifndef ONLINE_JUDGE
	freopen("in.txt","r",stdin);
#endif
	scanf("%d",&n);
	pre();
	double x,y;
	while(n--){
		tt=0;
		scanf("%lf %lf",&x,&y);a.x=x,a.y=y;
		scanf("%lf %lf",&x,&y);b.x=x,b.y=y;
		for(rg i=1;i<=t;++i)	cut(py[i],a,b);
		t=tt;
		for(rg i=1;i<=tt;++i)	py[i]=qy[i];
	}
//	for(int i=1;i<=t;++i){
//    	printf("$$%.2lf %.2lf\n",py[i].node[i].x,py[i].node[i].y);
//	}
	scanf("%d",&T);
	while(T--){
		scanf("%lf %lf",&x,&y);
		a.x=x,a.y=y;
		int ans=0;
		for(rg i=1;i<=t;++i){
			if(Vector::PIP(py[i].node,py[i].ncnt,a)==1)	++ans;
		}
		printf("%d\n",ans);
	}
	return 0;
} /*
2
-0.5 -0.5 1 1
1 75 0 75
6
10 60
80 60
30 40
10 10
50 50
20 50
*/

上一篇【学习笔记】【数学】斯特林数基础

下一篇【学习笔记】博弈论基础

posted @ 2023-08-08 16:57 Sonnety 阅读(105) 评论(3) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 【学习笔记】【数学】斯特林数基础

· 【ABC317】summary and solutions

· 【瞎口胡】计算几何基础

· 【计算几何】基础知识

· 【计算几何】All in All

阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 单线程的Redis速度为什么快？
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决：字节Trae VS Cursor，谁才是开发者新宠？
· 展开说说关于C#中ORM框架的用法！

$\mathcal{Namanyi\ Bruce}$

如果说，生命的脚步终有一天被时间的尘埃掩埋，那么我们就永远不能停下脚步。

【学习笔记】【数学】计算几何基础

前置知识：

叉积与跨立实验

例题：

[SCOI2007] 折纸

解题：

公告

常用链接

我的标签

随笔档案

相册

	il int dcmp(double a){
	if(a<-eps) return -1;
	if(a>eps) return 1;
	return 0;
	}
	il bool operator==(node a,node b)<% return !dcmp(a.x-b.x) && !dcmp(a.y-b.y); %>

	il node operator+(node a,node b)<% return node(a.x+b.x,a.y+b.y); %>
	il node operator-(node a,node b)<% return node(a.x-b.x,a.y-b.y); %>

	il double len(node a)<% return sqrt(dot(a,a)); %>
	//dot是点乘函数

	il Node footnode(Node p,Node a,Node b){
	Node x=p-a,y=p-b,z=b-a;
	double len1=Vector::dot(x,z)/Vector::len(z),len2=-1.0*Vector::dot(y,z)/Vector::len(z);
	return a+z*(len1/(len1+len2));
	}

	il int judge_cross(Node a,Node b,Node c,Node d){
	double c1=cro(b-a,c-a),c2=cro(b-a,d-a);
	double d1=cro(d-c,a-c),d2=cro(d-c,b-c);
	return mystd::dcmp(c1)mystd::dcmp(c2)<0 && mystd::dcmp(d1)mystd::dcmp(d2)<0;
	}

	il int PIP(Node *P,int n,Node a){
	int cnt=0,j;
	double res=0.0;
	for(rg i=1;i<=n;++i){
	if(i<n) j=i+1;
	else j=1;
	if(judge_line(a,P[i],P[j])) return 2;//点在多边形上
	if(a.y>=mystd::fMin(P[i].y,P[j].y) && a.y<mystd::fMax(P[i].y,P[j].y)){
	//纵坐标在该线段两端点之间
	res=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x);
	//res是同一纵坐标下的在该边上的点的横坐标
	cnt=cnt+(mystd::dcmp(res-a.x)>0);
	}
	}
	return cnt&1; //奇数次就是在多边形内
	}

	#include<bits/stdc++.h>
	using namespace std;
	#define rg register int
	#define il inline
	typedef long long ll;
	typedef long double llf;
	const double eps=1e-8;
	namespace mystd{
	il int Max(int a,int b)<%if(a<b) return b;return a; %>
	il int Min(int a,int b)<%if(a>b) return b;return a; %>
	il int Abs(int a)<% if(a<0) return a*(-1);return a; %>
	il double fMax(double a,double b)<%if(a<b) return b;return a; %>
	il double fMin(double a,double b)<%if(a>b) return b;return a; %>
	il double fAbs(double a)<% if(a<0) return a*(-1);return a; %>
	il int dcmp(double a){
	if(a<-eps) return -1;
	if(a>eps) return 1;
	return 0;
	}
	}
	struct Node<% double x,y; Node(double xx=0,double yy=0)<% x=xx,y=yy; %> %>;
	il bool operator==(Node a,Node b)<% return !mystd::dcmp(a.x-b.x) && !mystd::dcmp(a.y-b.y); %>
	il Node operator+(Node a,Node b)<% return Node(a.x+b.x,a.y+b.y); %>
	il Node operator-(Node a,Node b)<% return Node(a.x-b.x,a.y-b.y); %>
	il Node operator(Node a,double k)<% return Node(a.xk,a.y*k); %>
	namespace Vector{
	il double dot(Node a,Node b)<% return a.xb.x+a.yb.y; %> //点乘
	il double len(Node a)<% return sqrt(dot(a,a)); %> //模长
	il double angle(Node a,Node b)<% return acos(dot(a,b)/len(a)/len(b)); %>//夹角
	il double cro(Node a,Node b)<% return a.xb.y-a.yb.x; %> //叉积
	il int judge_LINE(Node p,Node a,Node b)<% return !mystd::dcmp(cro(p-a,b-a)); %>
	//判断p是否在直线AB上
	il int judge_line(Node p,Node a,Node b)<% return !mystd::dcmp(cro(p-a,b-a)) && mystd::dcmp(mystd::fMin(a.x,b.x)-p.x)<=0 && mystd::dcmp(p.y-mystd::fMax(a.y,b.y))<=0 && mystd::dcmp(p.x-mystd::fMax(a.x,b.x))<=0 && mystd::dcmp(mystd::fMin(a.y,b.y)-p.y)<=0; %>
	//判断p是否在线段AB上
	il Node footnode(Node p,Node a,Node b){
	Node x=p-a,y=p-b,z=b-a;
	double len1=dot(x,z)/len(z),len2=-1.0*dot(y,z)/len(z);
	return a+z*(len1/(len1+len2));
	}
	//求p到直线AB的垂足
	il Node symmetry(Node p,Node a,Node b)<% return p+(footnode(p,a,b)-p)*2; %>
	//求p到直线AB的对称点
	il Node internode(Node a,Node b,Node c,Node d)<% Node x=b-a,y=d-c,z=a-c;return a+x*(cro(y,z)/cro(x,y)); %>
	//直线AB与CD交点
	il int judge_CROSS(Node a,Node b,Node c,Node d)<% return judge_line(internode(a,b,c,d),c,d); %>
	//判断直线AB与线段CD是否有交点
	il int judge_cross(Node a,Node b,Node c,Node d){
	double c1=cro(b-a,c-a),c2=cro(b-a,d-a);
	double d1=cro(d-c,a-c),d2=cro(d-c,b-c);
	return mystd::dcmp(c1)mystd::dcmp(c2)<0 && mystd::dcmp(d1)mystd::dcmp(d2)<0;
	}
	//判断线段AB与线段CD是否有交点
	il int PIP(Node *P,int n,Node a){
	int cnt=0,j;
	double res=0.0;
	for(rg i=1;i<=n;++i){
	if(i<n) j=i+1;
	else j=1;
	if(judge_line(a,P[i],P[j])) return 2;//点在多边形上
	if(a.y>=mystd::fMin(P[i].y,P[j].y) && a.y<mystd::fMax(P[i].y,P[j].y)){
	//纵坐标在该线段两端点之间
	res=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x);
	//res是同一纵坐标下的在该边上的点的横坐标
	cnt=cnt+(mystd::dcmp(res-a.x)>0);
	}
	}
	return cnt&1; //奇数次就是在多边形内
	}
	//判断点a是否在多边形P内部
	}

	double multi(node p1, node p2, node p0) {
	double x1, y1, x2, y2;
	x1 = p1.x - p0.x;
	y1 = p1.y - p0.y;
	x2 = p2.x - p0.x;
	y2 = p2.y - p0.y;
	return x1 * y2 - x2 * y1;
	}

Namanyi BruceNamanyi Bruce\mathcal{Namanyi\ Bruce}

如果说，生命的脚步终有一天被时间的尘埃掩埋，那么我们就永远不能停下脚步。

【学习笔记】【数学】计算几何基础

前置知识：

叉积与跨立实验

例题：

[SCOI2007] 折纸

解题：

公告

常用链接

我的标签

随笔档案

相册

$\mathcal{Namanyi\ Bruce}$