【学习笔记】Manacher（马拉车）求回文子串

点击查看目录

目录

参考资料与图片来源

参考博客

我觉得这个博客讲的不好，他只讲看规律得到的结论，原因却不说，怪。

参考博客2

oi-wiki

算法思路

对于长度可能为奇可能为偶的情况，首先要预处理字符串，在每个字符左右增加一个无关字符 #。

\[\begin{aligned} &\text{bob}\\ &\downarrow\\ &\text{#b#o#b#}\\ \\ &\text{moon}\\ &\downarrow\\ &\text{#m#o#o#n#} \end{aligned} \]

这样字符串的长度就固定为奇数了。

接下来我们选定一个字符，以他为中心向左右扩展，求回文半径，如果只有其一个字符，半径为 \(1\)。

如：

\[\begin{aligned} &\text{# 1 # 2 # 2 # 1 # 2 # 2 #}\\ &1\ \ 2\ \ 1\ \ 2\ 5\ \ 2\ \ 1\ \ 6\ 1\ \ 2\ \ 3\ \ 2\ \ 1 \end{aligned} \]

或者：

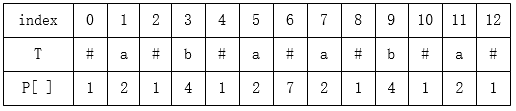
为什么要求回文半径？

以上面的 \(22122\) 为例子，其中心的 \(1\) 回文半径是 \(6\)，而该字符串原本的长度是 \(5\)。

这是一个普遍的规律：\(\left\lceil\frac{\text{原字符串长度}}{2}\right\rceil=\)回文中心左（包括回文中心）的字符串长度（即字符串回文半径）\(=\)回文中心左增加的 # 数。

设字符串回文半径长度为 \(P\)，那么加了#的字符串长度就为 \(2\times P-1\)，而分隔符是 \(P\) 个，故原字符串长度 \(T=2\times P-1-P=P-1\)

故，字符串回文长度=回文半径长度 \(-1\)。

现在我们就有了字符串长度，而由于第一个和最后一个字符都是#且需要搜索回文，所以为了防止越界，我们在前面加上一个非回文字符%，而后面就不用加了，因为结尾一定有一个字符'/0'。

（tips：越界例如：o 在 #b#o#b# 中的位置是 \(3\)，但是半径是 \(4\)，相减得起点为 \(-1\)，越界）

具体实现

最后就是如何求解我们的回文半径数组 \(P\) 的问题。

设 \(mi\) 是 \(i\) 位置之前回文长度能到达最远的右端点的回文串的重心位置，\(R\) 是最大回文串的能达到的右端点的值。

  • 若 \(i\leq R\)，我们可以找到 \(i\) 以 \(mi\) 为对称点对称到左边的位置 \(j=2\times mi-i\)。
  1. 若 \(P_j<R-i\)，那么证明 \(i\) 的回文没有超出 \(R\) 的边界，\(P_i=P_j\)。

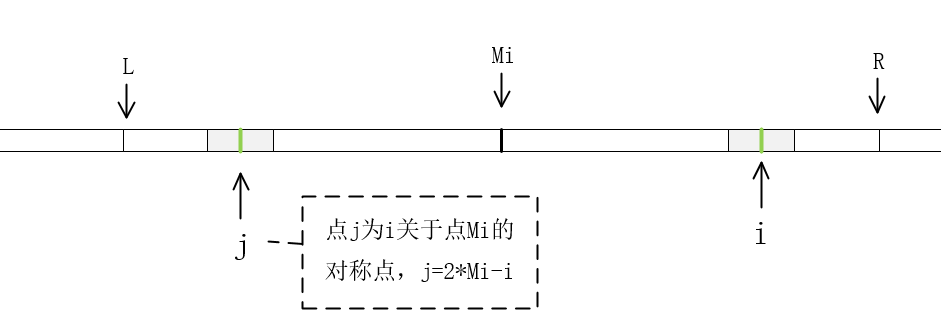
  1. 若 \(P_j\geq R-i\)，超出 \(R\) 的部分一个个和前面匹配。

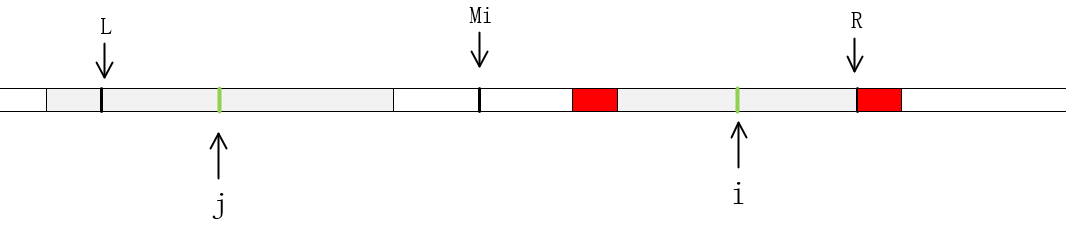
  • 若 \(i>R\)，那有什么办法，一一匹配呗。

时间复杂度 \(O(n)\)。

有代码：

Miku's Code 
string Manacher(string s){
    string res="$#";
    for(int i=0;i<s.size();++i){
        res+=s[i];
        res+="#";
    } 
	/*改造字符串*/
	/*数组*/
    vector<int> P;
    for(rg i=0;i<=res.size();++i)	P.push_back(0);
    int mi=0,right=0;   		//mi为最大回文串对应的中心点，right为该回文串能达到的最右端的值
    int maxLen=0,maxPoint=0;    //maxLen为最大回文串的长度，maxPoint为记录中心点
    for(int i=1;i<res.size();++i){
    	if(right>i)	P[i]=min(P[2*mi-i],right-i);
		else	P[i]=1; 
        while(res[i+P[i]]==res[i-P[i]])	++P[i];
        if(right<i+P[i]){
		//超过之前的最右端，则改变中心点和对应的最右端
            right=i+P[i];
            mi=i;
    	}
        if(maxLen<P[i]){
		//更新最大回文串的长度，并记下此时的点
            maxLen=P[i];
            maxPoint=i;
        }
    }
    return s.substr((maxPoint-maxLen)/2,maxLen-1);
    //在原串中提取最大回文子串 
}

然后将函数返回值改成 int 和 \(maxLen-1\) 就能切掉洛谷的模板题。

洛谷题目链接：模板Manacher

（似乎我过这道题的时候数据过水，但是新的 hack 并没有卡掉咱捏）

例题

Sonya and Matrix Beauty

题目链接

题面翻译

题目描述

一句话题意：给定一个 \(n \times m\) 的字符矩阵，请求出有多少个子矩阵在重排子矩阵每一行的字符后，使得子矩阵的每行每列都是回文串。

Sonya 最近过了生日，她收到一个 \(n \times m\) 的字符矩阵。

我们称一个子矩阵是美丽的，当且仅当在重新排列这个子矩阵每一行的字符后，使得这个子矩阵的每一行每一列都是回文串。

Sonya 想要知道这个矩阵中有几个子矩阵是美丽的。

输入格式

第一行两个整数 \(n,m\)，意义如上文所述。

接下来 \(n\) 行一行 \(m\) 个字符，表示这个子矩阵每一行的字符。

输出格式

一行一个整数，表示美丽的子矩阵数目

数据范围

对于 \(1 \leq m,n \leq 250\)

题目描述

Sonya had a birthday recently. She was presented with the matrix of size $ n\times m $ and consist of lowercase Latin letters. We assume that the rows are numbered by integers from $ 1 $ to $ n $ from bottom to top, and the columns are numbered from $ 1 $ to $ m $ from left to right.

Let's call a submatrix $ (i_1, j_1, i_2, j_2) $ $ (1\leq i_1\leq i_2\leq n; 1\leq j_1\leq j_2\leq m) $ elements $ a_{ij} $ of this matrix, such that $ i_1\leq i\leq i_2 $ and $ j_1\leq j\leq j_2 $ . Sonya states that a submatrix is beautiful if we can independently reorder the characters in each row (not in column) so that all rows and columns of this submatrix form palidroms.

Let's recall that a string is called palindrome if it reads the same from left to right and from right to left. For example, strings $ abacaba, bcaacb, a $ are palindromes while strings $ abca, acbba, ab $ are not.

Help Sonya to find the number of beautiful submatrixes. Submatrixes are different if there is an element that belongs to only one submatrix.

输入格式

The first line contains two integers $ n $ and $ m $ $ (1\leq n, m\leq 250) $ — the matrix dimensions.

Each of the next $ n $ lines contains $ m $ lowercase Latin letters.

输出格式

Print one integer — the number of beautiful submatrixes.

样例 #1

样例输入 #1

1 3
aba

样例输出 #1

4

样例 #2

样例输入 #2

2 3
aca
aac

样例输出 #2

11

样例 #3

样例输入 #3

3 5
accac
aaaba
cccaa

样例输出 #3

43

提示

In the first example, the following submatrixes are beautiful: $ ((1, 1), (1, 1)); ((1, 2), (1, 2)); $ $ ((1, 3), (1, 3)); ((1, 1), (1, 3)) $ .

In the second example, all submatrixes that consist of one element and the following are beautiful: $ ((1, 1), (2, 1)); $ $ ((1, 1), (1, 3)); ((2, 1), (2, 3)); ((1, 1), (2, 3)); ((2, 1), (2, 2)) $ .

Some of the beautiful submatrixes are: $ ((1, 1), (1, 5)); ((1, 2), (3, 4)); $ $ ((1, 1), (3, 5)) $ .

The submatrix $ ((1, 1), (3, 5)) $ is beautiful since it can be reordered as:

<br></br>accca<br></br>aabaa<br></br>accca<br></br>In such a matrix every row and every column form palindromes.

解题

题意概括：（给定一个 \(n \times m\) 的字符矩阵，求有多少个子矩阵在任意排列每一行内的字符后，使得子矩阵的每行每列都是回文串）

因为行是随意排列的，所以只要判断所在行内的字符出现次数为奇数的个数，若 \(\geq 2\) 则不合法。

所以我们可以把每一行的字符串看做一个字符，然后看列，如果一列成为一个字符串，那么关于这一列中心对称的两行应该是完全相同的，直接比较 \(26\) 个字母个数，跑一遍 Manacher 即可。

因为我们把每一行字符串看做了一个字符，所以其实可以对他们这一行进行 hash 对应，但是由于这道题并没有卡，所以我没有使用，但是我又想卡进最优解第一页，所以加了万能头和 getchar 读入字符串，可能某些校内 Oline Judge 不能使用。

（CF能用，现在在最优解第八个）

（比如说我们家 OJ 造的数据每个字符串结尾都不止一个换行，不能使用 getchar 读入字符串）

Miku's Code 
%:pragma GCC optimize(3)
%:pragma GCC optimize("Ofast")
%:pragma GCC optimize("inline")
%:pragma GCC optimize("-fgcse")
%:pragma GCC optimize("-fgcse-lm")
%:pragma GCC optimize("-fipa-sra")
%:pragma GCC optimize("-ftree-pre")
%:pragma GCC optimize("-ftree-vrp")
%:pragma GCC optimize("-fpeephole2")
%:pragma GCC optimize("-ffast-math")
%:pragma GCC optimize("-fsched-spec")
%:pragma GCC optimize("unroll-loops")
%:pragma GCC optimize("-falign-jumps")
%:pragma GCC optimize("-falign-loops")
%:pragma GCC optimize("-falign-labels")
%:pragma GCC optimize("-fdevirtualize")
%:pragma GCC optimize("-fcaller-saves")
%:pragma GCC optimize("-fcrossjumping")
%:pragma GCC optimize("-fthread-jumps")
%:pragma GCC optimize("-funroll-loops")
%:pragma GCC optimize("-fwhole-program")
%:pragma GCC optimize("-freorder-blocks")
%:pragma GCC optimize("-fschedule-insns")
%:pragma GCC optimize("inline-functions")
%:pragma GCC optimize("-ftree-tail-merge")
%:pragma GCC optimize("-fschedule-insns2")
%:pragma GCC optimize("-fstrict-aliasing")
%:pragma GCC optimize("-fstrict-overflow")
%:pragma GCC optimize("-falign-functions")
%:pragma GCC optimize("-fcse-skip-blocks")
%:pragma GCC optimize("-fcse-follow-jumps")
%:pragma GCC optimize("-fsched-interblock")
%:pragma GCC optimize("-fpartial-inlining")
%:pragma GCC optimize("no-stack-protector")
%:pragma GCC optimize("-freorder-functions")
%:pragma GCC optimize("-findirect-inlining")
%:pragma GCC optimize("-fhoist-adjacent-loads")
%:pragma GCC optimize("-frerun-cse-after-loop")
%:pragma GCC optimize("inline-small-functions")
%:pragma GCC optimize("-finline-small-functions")
%:pragma GCC optimize("-ftree-switch-conversion")
%:pragma GCC optimize("-foptimize-sibling-calls")
%:pragma GCC optimize("-fexpensive-optimizations")
%:pragma GCC optimize("-funsafe-loop-optimizations")
%:pragma GCC optimize("inline-functions-called-once")
%:pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
namespace io{
//	#if ONLINE_JUDGE 
//	char in[1<<20],*p1=in,*p2=in;
//	#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
//	#endif
//	有字符串,禁用fread 
	il int read(){
   		char c=getchar();
    	int x=0,f=1;
   		while(c<48)<%if(c=='-')f=-1;c=getchar();%>
    	while(c>47)x=(x*10)+(c^48),c=getchar();
    	return x*f;
	}
	il void write(int x){
    	if(x<0)<%putchar('-');x=~x+1;%>
    	if(x>9) write(x/10);
   		putchar(x%10+'0');
	} 
	il int ins(char *str){
		int len=0;
		while(1){
			char c=getchar();
			if(c!='\n' && c!='\0' && c!='\r')	str[++len]=c;
			else	break;
		}
		return len;
	}
}namespace mystd{
	il int Max(int a,int b)<%if(a<b) return b;return a; %>
	il int Min(int a,int b)<%if(a>b) return b;return a; %>
	il int Abs(int a)<% if(a<0) return a*(-1);return a; %>
	il double fMax(double a,double b)<%if(a<b) return b;return a; %>
	il double fMin(double a,double b)<%if(a>b) return b;return a; %>
	il double fAbs(double a)<% if(a<0) return a*(-1);return a; %>
	il int dcmp(double a){
		if(a<-eps)	return -1;
		if(a>eps)	return 1;
		return 0;
	}
}const int maxn=510;

int ttt;
int n,m,len[maxn],odd[maxn],cnt[maxn][30],f[maxn],ans;
char s[maxn][maxn];

il bool judge(int x,int y){
	if(odd[x]>1 || odd[y]>1)	return false;
	for(rg i=0;i<=25;++i)	if(cnt[x][i]!=cnt[y][i])	return false;
	return true;
}

il void clear(){
	for(rg i=0;i<=n;++i){
		odd[(i<<1)-1]=0;
		for(rg j=0;j<=25;++j)	cnt[(i<<1)-1][j]=0;
	}
}

il void work(){
	for(rg l=1;l<=m;++l){
		clear();
		for(rg r=l;r<=m;++r){
			for(rg i=1;i<=n;++i){
				int ch=s[i][r]-'a';
				++cnt[(i<<1)-1][ch];
				if(cnt[(i<<1)-1][ch]&1)	++odd[(i<<1)-1];
				else	--odd[(i<<1)-1];
			}
			for(rg i=0;i<=(n<<1);++i)	f[i]=0;	//回文半径 
			cnt[(n<<1)+1][0]=-1;
			int pos=0,R=0;
			for(rg i=1;i<=(n<<1);++i){
				if(odd[i]>1)	continue;
				if(R>i)	f[i]=mystd::Min(f[(pos<<1)-i],R-i);
				else	f[i]=1;
				while(judge(i-f[i],i+f[i])==true)	++f[i];
				if(i+f[i]>R){
					pos=i;
					R=pos+f[i];
				}
				ans+=f[i]/2;
			}
		}
	}
	io::write(ans);
}

il void input(){
	n=io::read(),m=io::read();
	for(rg i=1;i<=n;++i)	io::ins(s[i]);
}

int main(){
//	#if ONLINE_JUDGE
//	freopen("pal.in","r",stdin);
//	freopen("pal.out","w",stdout);
//	#endif
	input();
	work();
	return 0;
}
posted @ 2023-08-24 17:04  Sonnety  阅读(27)  评论(0)  编辑  收藏  举报