【学习笔记】二分图与网络流基础

二分图与网络流基础（网络流待学）

查看目录

目录

二分图：

二分图的定义：

对于一无向图，将该图分为两个点集，点集内部的点两两没有连边，则称该无向图为二分图，两个点集则是二分图的左部或右部。

较为数学的表示：

如果一张无向图 \((V,E)\) 存在点集 \(A,B\)，满足 \(|A|,|B| \ge 1\)，\(A \cap B = \varnothing\)，\(A \cup B = V\)，且对于 \(x,y \in A\) 或 \(x,y \in B\)，\((x,y) \notin E\)，则称这张无向图为一张二分图，\(A,B\) 分别为二分图的左部和右部。

二分图的判定：

一张图是二分图，当且仅当图中无奇环。

证明：每一条边都是从一个集合走到另一个集合，只有走偶数次才可能回到同一个集合。

因此可以考虑 \(dfs\) 染色，时间复杂度 \(O(n)\)，有代码：

Miku's Code 
int n,m;
bool vis[maxn];
int head[maxn<<1],t;
struct edge{
	int u,v;
	int next_;
};edge e[maxn<<1];
void add_edge(int u,int v){
	e[++t].u=u;
	e[t].v=v;
	e[t].next_=head[u];
	head[u]=t;
}

bool dfs(int now){
	vis[now]=true;
	for(int i=head[now];i;i=e[i].next_){
		int to=e[i].v;
		if(vis[to]==true)	return false;
		dfs(to);
	}
	return true;
}

void input(){
	scanf("%d %d",&n,&m);
	int u,v;
	for(int i=1;i<=m;++i){
		scanf("%d %d",&u,&v);
		add_edge(u,v);
		add_edge(v,u); 
	} 
}

int main(){
	input();
	if(dfs(1))	printf("YES\n");
	else	printf("NO\n");
	return 0;
}

例题：[NOIP2010 提高组] 关押罪犯

题目链接

[NOIP2010 提高组] 关押罪犯

折叠题面

题目描述

S 城现有两座监狱，一共关押着 \(N\) 名罪犯，编号分别为 \(1-N\)。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 \(c\) 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 \(c\) 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了\(N\) 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

输入格式

每行中两个数之间用一个空格隔开。第一行为两个正整数 \(N,M\)，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 \(M\) 行每行为三个正整数 \(a_j,b_j,c_j\)，表示 \(a_j\) 号和 \(b_j\) 号罪犯之间存在仇恨，其怨气值为 \(c_j\)。数据保证 \(1<a_j\leq b_j\leq N, 0 < c_j\leq 10^9\)，且每对罪犯组合只出现一次。

输出格式

共 \(1\) 行，为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出 0。

样例 #1

样例输入 #1

4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884

样例输出 #1

3512

提示

【输入输出样例说明】罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是 \(3512\)（由 \(2\) 号和 \(3\) 号罪犯引发）。其他任何分法都不会比这个分法更优。

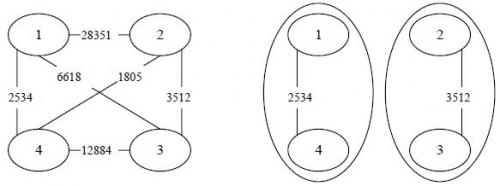
【数据范围】

对于 \(30\%\)的数据有 \(N\leq 15\)。

对于 \(70\%\) 的数据有 \(N\leq 2000,M\leq 50000\)。

对于 \(100\%\) 的数据有 \(N\leq 20000,M\leq 100000\)。

解题：

这道题可以用并查集做，这里说二分图做法。

一共两座监狱，而且要求监狱内的的矛盾较小，较为明显的二分图做法。

可以用两种颜色去标记图中的点，当一个节点被标记了一种颜色，与其相邻的点就是另一种颜色。

对于矛盾值，二分答案，大于等于枚举的答案的仇恨值连为一条边。

Miku's Code 
#include<bits/stdc++.h>
using namespace std;
#define rg register int
#define il inline
typedef long long ll;
typedef long double llf;
const double eps=1e-8;
namespace mystd{
	il int Max(int a,int b)<%if(a<b) return b;return a; %>
	il int Min(int a,int b)<%if(a>b) return b;return a; %>
	il int Abs(int a)<% if(a<0) return a*(-1);return a; %>
	il double fMax(double a,double b)<%if(a<b) return b;return a; %>
	il double fMin(double a,double b)<%if(a>b) return b;return a; %>
	il double fAbs(double a)<% if(a<0) return a*(-1);return a; %>
	il int dcmp(double a){
		if(a<-eps)	return -1;
		if(a>eps)	return 1;
		return 0;
	}
}
const int maxn=1e6+7;

int n,m,l,r;
int vis[maxn];
int head[maxn<<1],t;
struct edge{
	int u,v,w;
	int next_;
};edge e[maxn<<1];
void add_edge(int u,int v,int w){
	e[++t].u=u;
	e[t].v=v;
	e[t].w=w;
	e[t].next_=head[u];
	head[u]=t;
}

bool check(int mid){
	memset(vis,0,sizeof(vis));
	queue<int> q;
	while(!q.empty())	q.pop();
	for(int i=1;i<=n;++i){
		if(!vis[i]){
			q.push(i);
			vis[i]=1;
			while(!q.empty()){
				int now=q.front();
				q.pop();
				for(int i=head[now];i;i=e[i].next_){
					if(e[i].w>=mid){
						if(!vis[e[i].v]){
							q.push(e[i].v);
							if(vis[now]==1)	vis[e[i].v]=2;
							else	vis[e[i].v]=1;
						}
						else if(vis[e[i].v]==vis[now])	return false;
					}
				}
			}
		}
	}
	return true;
}

void input(){
	scanf("%d %d",&n,&m);
	int u,v,w;
	for(int i=1;i<=m;++i){
		scanf("%d %d %d",&u,&v,&w);
		r=mystd::Max(r,w);
		add_edge(u,v,w);
		add_edge(v,u,w); 
	}
}

int main(){
	input();
	int ans=0;
	r=r+1;
	while(l+1<r){
		int mid=(l+r)>>1;
		if(check(mid))	r=mid;
		else	l=mid;
	}
	printf("%d\n",l);
	return 0;
}

二分图的匹配：

给定⼀个⼆分图 \(G\)，\(M\) 为 \(G\) 边集的⼀个⼦集，如果满⾜当中的任意两条边都不依附于同⼀个顶点（没有公共端点），则称 \(M\) 是⼀个匹配，匹配的大小就是 \(M\) 中边的数量，称 匹配数，其中的边称 匹配边，点称 匹配点。

例如：

该图的#9999ff 色边集合和 #ff407a 色边集合均为二分图的匹配。

  • 二分图的最大匹配：

图中包含 边数最多 的匹配称为二分图的最大匹配。

  • 邻域：

设二分图 \(G=\{V_1,V_2,E\}\)，\(S\) 是二分图左部点 \(V_1\) 的子集，\(S\) 所连接的所有右部点的并集称为 \(S\) 的邻域，记为 \(N(S)=\Cup_{v_i\in S} N(v_i)\)。

  • 完美匹配：

设二分图 \(G=\{V_1,V_2,E\}\)，其中 \(|V_1|\leq |V_2|\)，\(M\) 是该二分图的最大匹配，且 \(|M|=|V_1|\)，称 \(M\) 是 \(V_1\) 到 \(V_2\) 的完美匹配。（也就是说 \(V_1\) 全部是匹配点）

匈牙利算法：

题目链接

折叠题干：

【模板】二分图最大匹配

题目描述

给定一个二分图，其左部点的个数为 \(n\)，右部点的个数为 \(m\)，边数为 \(e\)，求其最大匹配的边数。

左部点从 \(1\) 至 \(n\) 编号，右部点从 \(1\) 至 \(m\) 编号。

输入格式

输入的第一行是三个整数，分别代表 \(n\)，\(m\) 和 \(e\)。

接下来 \(e\) 行，每行两个整数 \(u, v\)，表示存在一条连接左部点 \(u\) 和右部点 \(v\) 的边。

输出格式

输出一行一个整数，代表二分图最大匹配的边数。

样例 #1

样例输入 #1

1 1 1
1 1

样例输出 #1

1

样例 #2

样例输入 #2

4 2 7
3 1
1 2
3 2
1 1
4 2
4 1
1 1

样例输出 #2

2

提示

数据规模与约定

对于全部的测试点，保证：

  • \(1 \leq n, m \leq 500\)。
  • \(1 \leq e \leq 5 \times 10^4\)。
  • \(1 \leq u \leq n\)，\(1 \leq v \leq m\)。

不保证给出的图没有重边。

定义说明：

  • 交错路：始于非匹配点，由非匹配边和匹配边交错组成的路径。（如下图，空心点和实心点分别表示二分图的两个点集，同一点集内点不能连边，#ff407a 色边是匹配边）

  • 增广路：始于非匹配点，终于非匹配点的交错路，路径长度一定为奇数。（如下图）

  • 增广：对于增广路，其非匹配边比匹配边多 \(1\)，将匹配边改成非匹配边，非匹配边改成匹配边，则匹配边数加 \(1\)，且依然是交错路，此过程称为增广。（如上图变为上上图的过程）

核心思想：枚举所有非匹配点，找增广路，对每一条增广路取反，直到找不到增广路。

算法实现：

  • 贪心，搜索递归。

  • 将匹配边集合置为空。

  • 找到一个增广路径 \(P\)，\(P\) 上的增广路全部取反得到一个更大的匹配。

  • 重复上一步直到找不到增广路。

算法演示：如图：

Miku's Code 
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
#if ONLINE_JUDGE
char in[1<<20],*p1=in,*p2=in;
#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#endif
inline int read(){
	char c=getchar();
    int x=0,f=1;
    while(c<48)<%if(c=='-')f=-1;c=getchar();%>
    while(c>47)x=(x*10)+(c^48),c=getchar();
    return x*f;
}const int maxn=1030;

int n,m,e,ans;
bool vis[maxn],g[maxn][maxn];
int match[maxn];

bool find(int x){
	for(rg j=1;j<=m;++j){
		if(!vis[j] && g[x][j]){
			vis[j]=true;
			if(!match[j] || find(match[j])){
				match[j]=x;
			 	return true;
			} 
		}
	}
	return false;
} 

int main(){
	n=read(),m=read(),e=read();
	int x,y;
	for(rg i=1;i<=e;++i){
		x=read(),y=read();
		g[x][y]=true;
	}
	for(rg i=1;i<=n;++i){
		memset(vis,false,sizeof(vis));
		if(find(i))	++ans;
	}
	printf("%d\n",ans);
	return 0;
}

时间复杂度：\(O(nm)\)。

Hall 定理

再次给出相关定义：

完美匹配：设二分图 \(G=\{V_1,V_2,E\}\)，其中 \(|V_1|\leq |V_2|\)，\(M\) 是该二分图的最大匹配，且 \(|M|=|V_1|\)，称 \(M\) 是 \(V_1\) 到 \(V_2\) 的完美匹配。（也就是说 \(V_1\) 全部是匹配点）

邻域：设二分图 \(G=\{V_1,V_2,E\}\)，\(S\) 是二分图左部点 \(V_1\) 的子集，\(S\) 所连接的所有右部点的并集称为 \(S\) 的邻域，记为 \(N(S)=\Cup_{v_i\in S} N(v_i)\)。

因此有霍尔定理：设二分图 \(G=\{V_1,V_2,E\}\)，\(|V_1|\leq |V_2|\)，则 \(G\) 存在 \(V_1\) 到 \(V_2\) 的完美匹配当且仅当对于任意的 \(S\subset V_1\)，均存在 \(|S|\leq |N(S)|\)。

简单证明：

  • 必要性：

如果点集 \(S\) 的邻域 \(|N(S)|\leq |S|\)，则一定存在某几条边在子集 \(S\) 中有共同端点，不符合二分图定义，子集 \(S\) 不能形成完美匹配。

所以如果形成了完美匹配，则一定满足任意的 \(S\subset V_1\)，均存在 \(|S|\leq |N(S)|\)。

  • 充分性：

考虑使用归纳法证明：

  1. 如果存在子集 \(S\)，其邻域 \(|N(S)|=|S|\)，那么这个子集本身就是完美匹配。

    所以把 \(S\) 和 \(N(S)\) 删掉，如果存在不满足条件的集合 \(T\)，那么就存在 \(|S\cup T|>|N(S\cup T)|\)，与二分图矛盾。

    所以不存在满足条件的集合 \(T\)，当存在 \(|S|=|N(S)|\) 时，霍尔定理成立。

  2. 如果所有子集的 \(|N(S)|>|S|\)，那么在左部点 \(S_1\) 随意找一个点 \(u\)，一条边 \((u,v)\in E\)，那么删去 \(u\) 点和 \(v\) 点以及两点连接的所有边。

    因为 \(S\) 删掉的点一定小于等于 \(N(S)\) 删去的点+1，所以能够满足 \(|N(S)|\geq |S|\)，根据归纳法，霍尔定理成立。

网络流

更多的有关网络流的名词定义

个人认为网络流题目重点在于建模问题，而建模问题建议刷典题。

推荐：网络流题目汇总

最大流

【模板】网络最大流

折叠题干

【模板】网络最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入格式

第一行包含四个正整数 \(n,m,s,t\)，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来 \(m\) 行每行包含三个正整数 \(u_i,v_i,w_i\)，表示第 \(i\) 条有向边从 \(u_i\) 出发，到达 \(v_i\)，边权为 \(w_i\)（即该边最大流量为 \(w_i\)）。

输出格式

一行，包含一个正整数，即为该网络的最大流。

样例 #1

样例输入 #1

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 30

样例输出 #1

50

提示

样例输入输出 1 解释

题目中存在 \(3\) 条路径：

  • \(4\to 2\to 3\)，该路线可通过 \(20\) 的流量。
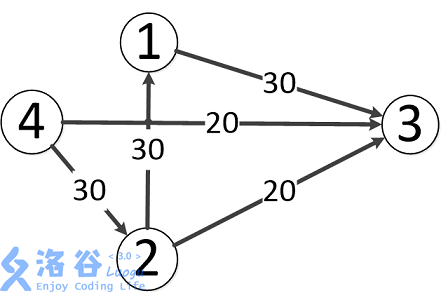
  • \(4\to 3\)，可通过 \(20\) 的流量。
  • \(4\to 2\to 1\to 3\)，可通过 \(10\) 的流量（边 \(4\to 2\) 之前已经耗费了 \(20\) 的流量）。

故流量总计 \(20+20+10=50\)。输出 \(50\)。

数据规模与约定

  • 对于 \(30\%\) 的数据，保证 \(n\leq10\)，\(m\leq25\)。
  • 对于 \(100\%\) 的数据，保证 \(1 \leq n\leq200\)，\(1 \leq m\leq 5000\)，\(0 \leq w\lt 2^{31}\)。

在最大流的题目中，有向图 即“容量网络”，有向边称为“弧”，其边权即“弧的容量”（称为 \(c(u,v)\)），其实际流量为“弧的流量”（称为 \(f(u,v)\)），流的起点被称为“源点”，终点被称为“汇点”。

因此最大流题目就可以翻译成：源点有无限的水，每条边单位时间内只能运输这条边容量大小的水，问单位时间内，终点可以汇聚最多多少水。

因此就引出了最大流的定义：

最大流是指网络中满足弧流量限制条件和平衡条件且具有最大流量的可行流。

其中：

  • 弧流量限制条件：流量要大于等于 \(0\)，且小于弧的容量。

  • 平衡条件：流量仅从源点流出，汇点汇聚，在网络中不凭空消失或凭空出现。

满足以上两点的就是可行流。

Edmonds-Karp 增广路算法

这里的增广路和二分图的增广路不同，给出定义：

  • 边 \(u\to v\) 的剩余容量：\(c(u,v)-f(u,v)\)。

  • 若一条从源点 \(S\) 到汇点 \(T\) 的路径上各条边的剩余容量都大于 \(0\)，称这条路径是一条增广路。

因此，增广路有一个最大流量 \(minf\)，其大小是边集中最小剩余容量的边的剩余容量。

因此 \(\mathtt{EK}\) 算法就是不断用 \(\mathtt{BFS}\) 寻找增广路，使网络流量增加 \(minf\)，直到网络上不存在增广路时为止。

而对于一条边，其可能被包含在多条增广路径中，我们要使其遍历可以“反悔”或者“回溯”以遍历所有的增广路。

因此对于 \(u\to v\) 的边，我们可以建立 \(v\to u\) 的反向边，使更新时，可以反悔。

如：\(c(u,v)=1,c(v,u)=0\)，在 \(\mathtt{BFS}\) 遍历后，\(c(u,v)=0,c(v,u)=1\)，重新更新的时候，我们可以通过走反边再次令 \(c(u,v)=1,c(v,u)=0\)。

为了遍历每一条正向边和反向边，我们可以通过邻接表的“成对储存”技巧实现，将每条有向边和反向边存储在邻接表下标为“\(2\) 和 \(3\)”、“\(4\) 和 \(5\)”，诸如此类的位置上，因此就可以通过 \(i \oplus 1\) 的形式找到 边\(i\) 对应的反向边或正向边。

代码来说，即是：

il void update(){
	int x=t;
	while(x!=s){
		int i=pre[x];
		e[i].w-=dis[t];
		e[i^1].w+=dis[t];
		x=e[i^1].v;
	}
	ans+=dis[t];
}

极限时间复杂度 \(O(nm^2)\)，一般可处理规模为 \(10^3-10^4\) 的网络。

对于本题，特别注意：开long long，去重边。

Miku's Code 
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define int long long
#define rg register int
#define MYMAX 200708310309393939
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
#if ONLINE_JUDGE 
char in[1<<20],*p1=in,*p2=in;
#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#endif
inline int read(){
    char c=getchar();
    int x=0,f=1;
    while(c<48)<%if(c=='-')f=-1;c=getchar();%>
    while(c>47)x=(x*10)+(c^48),c=getchar();
    return x*f;
}
const int maxn=2050,maxm=5030;

int n,m,s,t,dis[maxn],pre[maxn],ans;
int mj[maxn][maxn];
bool vis[maxn];
int tt=1,head[maxm<<1];
#define next Miku
struct edge{
	int v,w;
	int next;
};edge e[maxm<<1];
il void add_edge(int u,int v,int w){
	e[++tt].v=v;e[tt].w=w;e[tt].next=head[u];head[u]=tt;
	e[++tt].v=u;e[tt].w=0;e[tt].next=head[v];head[v]=tt;
}

il bool bfs(){
	memset(vis,false,sizeof(vis));
	queue<int> q;
	while(!q.empty())	q.pop();
	q.push(s);vis[s]=true;
	dis[s]=MYMAX;
	while(!q.empty()){
		int x=q.front();q.pop();
		for(rg i=head[x];i;i=e[i].next){
			if(e[i].w!=0 && vis[e[i].v]==false){
			//找增广路,只找剩余流量>0且未访问的边 
				int to=e[i].v;
				vis[to]=true;
				dis[to]=min(dis[x],e[i].w);
				pre[to]=i;//记录前驱,便于修改边权
				q.push(to);
				if(to==t)	return 1;
			}
		}
	}
	return 0;
}

il void update(){
	int x=t;
	while(x!=s){
		int i=pre[x];
		e[i].w-=dis[t];
		e[i^1].w+=dis[t];
		x=e[i^1].v;
	}
	ans+=dis[t];
}

il void input(){
	n=read(),m=read(),s=read(),t=read();
	int u,v,w;
	for(rg i=1;i<=m;++i){
		u=read(),v=read(),w=read();
		if(mj[u][v]==0){
			add_edge(u,v,w);
			mj[u][v]=tt;
		}
		else{
			e[mj[u][v]-1].w+=w;
		}
		//去重边操作 
	}
}

signed main(){
	input();
	while(bfs())	update();
	printf("%lld\n",ans);
	return 0;
}

Dinic算法

  • 残量网络：在任意时刻，网络中所有节点以及剩余容量大于 \(0\) 的边构成的子图被称为 残量网络。

\(\mathtt{EK}\) 算法每轮会遍历整个残量网络，但是却只找到一条增广路，因此时间复杂度拉跨。

我们想要一次找到多条增广路，这就是 \(\mathtt{Dinic}\) 算法。

分层图：我们可以求一个节点的深度 \(dep_x\)，而在残量网络中，满足 \(dep_y=dep_x+1\) 的边 \(E(x,y)\) 构成的子图就被称为分层图，它是一个有向无环图。

Dinic 算法不断重复：

  • 在残量网络上 \(\mathtt{BFS}\) 求出节点的层次，构造分层图。

  • 在分层图上 \(\mathtt{DFS}\) 寻找增广路，在回溯时实时更新剩余容量。

也就是对于一个分层图，找到多条增广路。

而 \(\mathtt{Dinic}\) 算法还可以应用剪枝和 当前弧优化：

  • 当前弧优化：直接从可以增加流量的边开始。

如上图， #ff407a色 的边表示当前流量已满，不能再增加流量，而 #39c5bb色 的边表示还可以继续增加流量。

而进行 \(\mathtt{BFS}\) 找分层图和 \(\mathtt{DFS}\) 找增广路时，流量已满的边 \(1\) 和 \(2\) 是不需要考虑的，这就是当前弧优化。

因此我们借助一个数组 \(now\) 来实现，其初始值就是 \(head\) 数组，在 \(dfs\) 时，从 \(u\) 点访问了第 \(i\) 条边，证明对于当前分层图来说，前面的 \(i-1\) 条边流量已满，直接修改 \(now_u=i\)，下次再访问 \(u\) 点时，直接从 第 \(i\) 条边开始。

考虑算法的优劣，事实上，\(\mathtt{Dinic}\) 最大流的 \(\mathtt{DFS}\) 部分会遍历整张图找到多条可行的最短路，但是 \(\mathtt{EK}\) 最大流算法只会把一条从源点到汇点的路径记录，节省了扫描整张图的时间。

事实上，我认为，直接讨论谁到底更优是不合适的，对于不同的数据来说，当增广路较短的，较多的图出现，如二分图的时候，\(\mathtt{Dinic}\) 就会突出其优越性，相反，在增广路较长时，\(\mathtt{EK}\) 就更占上风。

所以在随机数据下，\(\mathtt{Dinic}\) 大概是优于 \(\mathtt{EK}\) 的。

\(\mathtt{Dinic}\) 算法极限时间复杂度为 \(O(n^2m)\)，通常可以处理 \(10^4-10^5\) 规模的网络。

特别的，Dinic 算法求解二分图最大匹配时，建立超级源点和超级汇点，时间复杂度为优秀的 \(O(m\sqrt{n})\)。（求二分图最大匹配具体实现见下题）

Miku's Code 
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
#if ONLINE_JUDGE
char in[1<<25],*p1=in,*p2=in;
#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#endif
inline ll read(){
    char c=getchar();
    ll x=0,f=1;
    while(c<48)<%if(c=='-')f=-1;c=getchar();%>
    while(c>47)x=(x*10)+(c^48),c=getchar();
    return x*f;
}const int maxn=2050,maxm=5030;
const ll MYMAX=2007083103093939;

int n,m,s,t,dep[maxn],now[maxn];
ll w,ans,dis[maxn];
int tt=1,head[maxm<<1];
#define next Miku
struct edge{
	int v;
	ll w;
	int next;
};edge e[maxm<<1];
il void add_edge(int u,int v,ll w){
	e[++tt].v=v;e[tt].w=w;e[tt].next=head[u];head[u]=tt;
	e[++tt].v=u;e[tt].w=0;e[tt].next=head[v];head[v]=tt; 
}

il void clear(){
	for(rg i=1;i<=n;++i)	dep[i]=0;
}

il bool bfs(){
//在残量网络上构造分层图
	clear();
	queue<int> q;
	while(!q.empty())	q.pop();
	q.push(s);
	dep[s]=1;
	now[s]=head[s];
	while(!q.empty()){
		int x=q.front();q.pop();
		for(rg i=head[x];i;i=e[i].next){
			int to=e[i].v;
			if(e[i].w>0 && dep[to]==0){
				q.push(to);
				now[to]=head[to];
				dep[to]=dep[x]+1;
				if(to==t)	return true;
			}
		}
	}
	return false;
}

ll dfs(int x,ll flow){
	if(x==t || flow==0)	return flow;
	ll rest,res=0;		//rest表示当前最小的剩余容量即增广路的最大流量 
	for(rg i=now[x];i && flow;i=e[i].next){
		now[x]=i;		//当前弧优化 
		int to=e[i].v;
		if(e[i].w>0 && dep[to]==dep[x]+1){
			rest=dfs(to,min(flow,e[i].w));
			if(rest==0) dep[to]=0;		//剪枝，去掉增广完毕的点
			e[i].w-=rest;
			e[i^1].w+=rest;
			res+=rest;					//res表示经过该点的所有流量和 
			flow-=rest;					//flow表示经过点是剩余流量
            if(flow==0)  break;
		}
	}
	return res;
}

il void input(){
	n=read(),m=read(),s=read(),t=read();
	int u,v,w;
	for(rg i=1;i<=m;++i){
		u=read(),v=read(),w=read();
		add_edge(u,v,w);
	}
}

int main(){
	input();
	while(bfs()){
		ans+=dfs(s,MYMAX); 
	} 
	printf("%lld\n",ans);
	return 0;
}

例题：[ABC317G] Rearranging

题目链接

[ABC317G] Rearranging

折叠题面

[ABC317G] Rearranging

题目描述

$ N $ 行 $ M $ 列のグリッドがあります。上から $ i $ 行目左から $ j $ 列目のマスには整数 $ A_{i,j} $ が書かれています。
ここで、グリッドのマスに書かれている計 $ NM $ 個の整数は $ 1,\ldots,N $ をちょうど $ M $ 個ずつ含みます。

あなたは次の手順でマスに書かれた数を入れ替える操作を行います。

  • $ i=1,\ldots,N $ の順に次を行う。
    • $ i $ 行目に書かれた数を自由に並び替える。すなわち、$ 1,\ldots,M $ の並び替えである長さ $ M $ の数列 $ P=(P_{1},\ldots,P_{M}) $ を自由に選び、$ A_{i,1},\ldots,A_{i,M} $ を 同時に $ A_{i,P_{1}},\ldots,A_{i,P_{M}} $ に置き換える。

あなたの目的は、操作後に全ての列が $ 1,\ldots,N $ を $ 1 $ つずつ含むようにすることです。そのようなことが可能であるか判定し、可能であれば操作後のグリッドの状態を出力してください。

翻译：（提供：我）

现有一个 \(N\) 行 \(M\) 列的矩阵，从上往下数第 \(i\) 行，从左往右数第 \(j\) 列的元素是 \(A_{i,j}\)。

对于 \(i=1,\ldots,n\)，你可以自由排列第 \(i\) 行的数字。

要求每一列包含 \(1,\ldots,N\) 一次（不要求顺序，包含即可），若可能，输出 Yes，并打印结果表格，否则，输出 No。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ M $ $ A_{1,1} $ $ \ldots $ $ A_{1,M} $ $ \vdots $ $ A_{N,1} $ $ \ldots $ $ A_{N,M} $

输出格式

操作により全ての列が $ 1,\ldots,N $ を $ 1 $ つずつ含むようにするのが不可能ならば No と出力せよ。
可能であるとき、$ 1 $ 行目に Yes と出力し、続く $ N $ 行に、全ての列が $ 1,\ldots,N $ を $ 1 $ つずつ含むように操作したあとのグリッドの状態を次の形式で出力せよ。
グリッドの上から $ i $ 行目左から $ j $ 列目のマスに書かれた数を $ B_{i,j} $ とする。各 $ 1\leq\ i\ \leq\ N $ について $ i+1 $ 行目に $ B_{i,1},\ldots,B_{i,M} $ をこの順に空白区切りで出力せよ。

答えが複数存在する場合、どれを出力しても正解とみなされる。

样例 #1

样例输入 #1

3 2
1 1
2 3
2 3

样例输出 #1

Yes
1 1
3 2
2 3

样例 #2

样例输入 #2

4 4
1 2 3 4
1 1 1 2
3 2 2 4
4 4 3 3

样例输出 #2

Yes
1 4 3 2
2 1 1 1
4 2 2 3
3 3 4 4

提示

制約

  • $ 1\ \leq\ N,M\ \leq\ 100 $
  • $ 1\ \leq\ A_{i,j}\ \leq\ N $
  • 入力は全て整数である
  • $ NM $ 個の数 $ A_{1,1},\ldots,A_{N,M} $ は $ 1,\ldots,N $ をそれぞれちょうど $ M $ 個ずつ含む

Sample Explanation 1

この他、以下の出力も正解とみなされる。 Yes 1 1 2 3 3 2

解题：

其实官方题解写的还是很清楚的。（但是思路好难想啊~）

我们建立二分图的子集，左边的子集代表 \(1,\ldots,n\) 行，右边的子集代表 \(1,\ldots,n\) 个数，共 \(2n\) 个点，显然子集内点没有连边，它是二分图。

而该行内有哪些数就从左子集的代表行的点连向右子集代表数的点连边，有几个连几次。

如样例 #1：

input:

3 2
1 1
2 3
2 3

因此可以找一个图的最大匹配，对于某一列，我们就得到了其数，如#9999ff 色边，其为一列：

1
2
3

然后再删去已经找到过的边，继续找最大匹配，即可。

output:

Yes
1 1
3 2
2 3

需要注意的是，已经找到过的二分图增广路会变成反边，找反边并删去即可，但是对于超级源点和超级汇点所建边，是不能变的。

Miku's code 
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define rg register int
#define MYMAX 20070831
typedef long double llf;
typedef long long ll;
typedef pair<int,int> PII;
const double eps=1e-8;
#if ONLINE_JUDGE
char in[1<<20],*p1=in,*p2=in;
#define getchar() (p1==p2&&(p2=(p1=in)+fread(in,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#endif
inline int read(){
	char c=getchar();
    int x=0,f=1;
    while(c<48)<%if(c=='-')f=-1;c=getchar();%>
    while(c>47)x=(x*10)+(c^48),c=getchar();
    return x*f;
}const int maxn=205,maxm=40050;

int now[maxm<<1],head[maxm<<1],tt=1;
#define next Miku
struct edge{
	int v,w,next;
};edge e[maxm<<1];
il void add_edge(int u,int v,int w){
	e[++tt].v=v;e[tt].w=w;e[tt].next=head[u];head[u]=tt;
	e[++tt].v=u;e[tt].w=0;e[tt].next=head[v];head[v]=tt;
}

int s,t,savt;
int n,m,dep[maxn],ans[maxn][maxn];

il void clear(){
	for(rg i=1;i<=(n<<1|1);++i)	dep[i]=0;
}

il bool bfs(){
	clear();
	queue<int> q;
	while(!q.empty())	q.pop();
	q.push(s);
	dep[s]=1;
	now[s]=head[s];
	while(!q.empty()){
		int x=q.front();q.pop();
		for(rg i=head[x];i;i=e[i].next){
			int to=e[i].v;
			if(e[i].w>0 && dep[to]==0){
				q.push(to);
				now[to]=head[to];
				dep[to]=dep[x]+1;
				if(to==t)	return true;
			}
		}
	}
	return false;
}

int dfs(int x,int flow){
	if(x==t)	return flow;
	int rest,res=0;
	for(rg i=head[x];i;i=e[i].next){
		int to=e[i].v;
		if(e[i].w>0 && dep[to]==dep[x]+1){
			rest=dfs(to,min(flow,e[i].w));
			if(rest==0)	dep[to]=0;
			e[i].w-=rest;
			e[i^1].w+=rest;
			res+=rest;
			flow-=rest;
		}
	}
	return res;
}

il int get_maxflow(){
	int ans=0;
	while(bfs())<% ans+=dfs(s,MYMAX); %>
	return ans;
}

il void input(){
	n=read(),m=read();
	t=(n<<1|1);
	int num;
	for(rg i=1;i<=n;++i){
		for(rg j=1;j<=m;++j){
			num=read();
			add_edge(i,n+num,1);
		}
	}
	savt=tt;
	for(rg i=1;i<=n;++i)<% add_edge(s,i,1);add_edge(n+i,t,1); %>
}

int main(){
	input();
	for(rg j=1;j<=m;++j){
		int flow=get_maxflow();
		if(flow!=n)	<% puts("No");return 0; %>
		for(rg i=3;i<=savt;i+=2){
		//网络流将匹配转为反边,枚举反边	
			if(e[i].w){
				int u=e[i].v,to=e[i^1].v;
//				cout<<"i="<<i<<"; u="<<u<<"; j="<<j<<"; to="<<to<<endl;
				ans[u][j]=to-n;
				e[i].w=0;
			}
		}
		for(rg i=savt+2;i<=tt;i+=2){
			if(e[i].w){
				e[i^1].w=1;
				e[i].w=0;
			}
		}
	}
	puts("Yes");
	for(rg i=1;i<=n;++i){
		for(rg j=1;j<=m;++j)	printf("%d ",ans[i][j]);
		putchar('\n');
	}
	return 0;
}

最小割

最小割问题就是对于一个有向图，选择一些边使图不联通，这个边集最小的边权和（容量和）就是最小割。

于是有最大流最小割定理，具体为：

  • 任何一个流一定小于等于任何一个割

显然，对于任何一个流，其流量不大于在其中的任何一条边的容量，而你随便割一条边一定大于等于其流量。

  • 一定存在一个流等于一个割

当达到最大流时，根据增广路定理，残留网络中 \(s\) 到 \(t\) 已经没有通路了，否则还能继续增广。

我们把 \(s\) 能到的的点集设为 \(S\),不能到的点集为 \(T\)。

构造出一个割集 \(C[S,T]\),\(S\) 到 \(T\) 的边必然满流，否则就能继续增广。

这些满流边的流量和就是当前的流即最大流。

故最大流等于最小割。

费用流

【模板】最小费用最大流

折叠题干

【模板】最小费用最大流

题目描述

给出一个包含 \(n\) 个点和 \(m\) 条边的有向图（下面称其为网络） \(G=(V,E)\)，该网络上所有点分别编号为 \(1 \sim n\)，所有边分别编号为 \(1\sim m\)，其中该网络的源点为 \(s\)，汇点为 \(t\)，网络上的每条边 \((u,v)\) 都有一个流量限制 \(w(u,v)\) 和单位流量的费用 \(c(u,v)\)。

你需要给每条边 \((u,v)\) 确定一个流量 \(f(u,v)\)，要求：

  1. \(0 \leq f(u,v) \leq w(u,v)\)（每条边的流量不超过其流量限制）；
  2. \(\forall p \in \{V \setminus \{s,t\}\}\)，\(\sum_{(i,p) \in E}f(i,p)=\sum_{(p,i)\in E}f(p,i)\)（除了源点和汇点外，其他各点流入的流量和流出的流量相等）；
  3. \(\sum_{(s,i)\in E}f(s,i)=\sum_{(i,t)\in E}f(i,t)\)（源点流出的流量等于汇点流入的流量）。

定义网络 \(G\) 的流量 \(F(G)=\sum_{(s,i)\in E}f(s,i)\)，网络 \(G\) 的费用 \(C(G)=\sum_{(i,j)\in E} f(i,j) \times c(i,j)\)。

你需要求出该网络的最小费用最大流，即在 \(F(G)\) 最大的前提下，使 \(C(G)\) 最小。

输入格式

输入第一行包含四个整数 \(n,m,s,t\)，分别代表该网络的点数 \(n\)，网络的边数 \(m\)，源点编号 \(s\)，汇点编号 \(t\)。

接下来 \(m\) 行，每行四个整数 \(u_i,v_i,w_i,c_i\)，分别代表第 \(i\) 条边的起点，终点，流量限制，单位流量费用。

输出格式

输出两个整数，分别为该网络的最大流 \(F(G)\)，以及在 \(F(G)\) 最大的前提下，该网络的最小费用 \(C(G)\)。

样例 #1

样例输入 #1

4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5

样例输出 #1

50 280

提示

对于 \(100\%\) 的数据，\(1 \leq n \leq 5\times 10^3\)，\(1 \leq m \leq 5 \times 10^4\)，\(1 \leq s,t \leq n\)，\(u_i \neq v_i\)，\(0 \leq w_i,c_i \leq 10^3\)，且该网络的最大流和最小费用 \(\leq 2^{31}-1\)。

输入数据随机生成。

（之前概念不再重复描述）

给出一个求最大流的网络模型，在每条边 \(E(x,y)\) 有属性 \(c(x,y)\) 的容量的前提下，增加了属性 \(w(x,y)\)，表示“单位费用”，即当边 \(E(x,y)\) 流量为 \(f(x,y)\) 时，需要花费费用 \(f(x,y)\times w(x,y)\)。

而在是最大流的前提下，总花费最小的流是“最小费用最大流”，总花费最大的流是 “最大费用最大流”，合称 费用流。

类似于最大流可以求二分图最大匹配，费用流也可以求二分图带权最大匹配。

Edmonds-Karp 增广路算法

\(\mathtt{EK}\) 算法求解最大流，使用 \(\mathtt{BFS}\) 寻找的增广路实际上是包含边数最少的增广路，因此我们只需要改成使用 \(\mathtt{SPFA}\) 找到费用之和最小的增广路即可，相应的，我们的反边的费用应该建为 \(-w(x,y)\)，而 \(\mathtt{dijkstra}\) 因为不能处理负边权而必须特殊处理。

Miku's Code 
#include<bits/stdc++.h>
#define il inline
#define rg register int
#define cout std::cout
#define cerr std::cerr
#define push_back emplace_back
#define make_pair std::make_pair
#define endl '\n'
#define bits(x) std::bitset<x>
typedef long long ll;
typedef unsigned long long ull;
typedef double ff;
typedef long double llf;
typedef unsigned char byte;
typedef std::pair<int,int> PII;
const ff eps=1e-8;
int Max(int x,int y){ return x<y?y:x; }
int Min(int x,int y){ return x<y?x:y; }
int Abs(int x){ return x>0?x:-x; }
il int read(){
    char c=getchar();int x=0,f=1;
    while(c<48) { if(c=='-')f=-1;c=getchar(); }
    while(c>47) x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x*f;
}const int maxn=5e3+5,maxm=5e4+5,inf=0x3f3f3f3f;

int n,m,S,T,dis[maxn],incf[maxn],pre[maxn],maxflow,ans;
bool vis[maxn];
int head[maxm<<1],t=1;
struct Edge{ int v,c,w;int next; };Edge e[maxm<<1];
il void add_edge(int u,int v,int c,int w){
    e[++t].v=v;e[t].c=c;e[t].w=w;e[t].next=head[u];head[u]=t;
    e[++t].v=u;e[t].c=0;e[t].w=-w;e[t].next=head[v];head[v]=t;
}

il bool SPFA(){
    std::queue<int> q;while(!q.empty()) q.pop();
    for(rg i=0;i<=n;++i)    dis[i]=inf,vis[i]=false;
    q.push(S);vis[S]=true;dis[S]=0;incf[S]=inf;
    while(!q.empty()){
        int now=q.front();vis[now]=false;q.pop();
        for(rg i=head[now];i;i=e[i].next){
            int to=e[i].v;
            if(e[i].c && dis[to]>dis[now]+e[i].w){
                dis[to]=dis[now]+e[i].w;incf[to]=Min(incf[now],e[i].c);pre[to]=i;
                if(!vis[to])    q.push(to),vis[to]=true;
            }
        }
    }
    if(dis[T]==inf)    return false;
    return true;
}

il void update(){
    int now=T;
    while(now!=S){
        int i=pre[now];
        e[i].c-=incf[T];
        e[i^1].c+=incf[T];
        now=e[i^1].v;
    }
    maxflow+=incf[T];ans+=dis[T]*incf[T];
}

il void input(){
    n=read(),m=read(),S=read(),T=read();int u,v,c,w;
    for(rg i=1;i<=m;++i){
        u=read(),v=read(),c=read(),w=read();
        add_edge(u,v,c,w);
    }
}

int main(){
freopen("EK.in","r",stdin);
    input();
    while(SPFA())   update();    
    printf("%d %d\n",maxflow,ans);
    return 0;
}
// Oh pick yourself up 'cause
// SPFA never die

zkw 费用流

就是把 \(\mathtt{Dinic}\) 的 \(\mathtt{BFS}\) 改成 \(\mathtt{SPFA}\) 即可。

但是因为存在负边权，\(\mathtt{zkw}\) 费用流增广时可行边组成的图，不一定是有向无环图。

但是 \(\mathtt{DFS}\) 时需要注意一点，就是我们可行边构成的图不一定是一个 \(\mathtt{DAG}\)，我们可以从一个负边来回递归，所以必须加入 \(vis\) 数组判断是否经过，回溯的时候再撤销。

而对于非分层图来说，当前弧优化会使得提前跳出 \(\mathtt{DFS}\) 的过程，进行新一轮 \(\mathtt{SPFA}\)，增加了遍历次数，不优。

至于算法的优劣分析，和上文对 \(\mathtt{Dinic}\) 的分析类似。

（闲话：发现求费用流好像比 \(\mathtt{EK}\) 快不了多少，可能是我写法的问题，我还是更喜欢 \(\mathtt{EK}\)）

Miku's Code 
#include<bits/stdc++.h>
#define il inline
#define rg register int
#define cout std::cout
#define cerr std::cerr
#define push_back emplace_back
#define make_pair std::make_pair
#define endl '\n'
#define bits(x) std::bitset<x>
typedef long long ll;
typedef unsigned long long ull;
typedef double ff;
typedef long double llf;
typedef unsigned char byte;
typedef std::pair<int,int> PII;
const ff eps=1e-8;
int Max(int x,int y){ return x<y?y:x; }
int Min(int x,int y){ return x<y?x:y; }
int Abs(int x){ return x>0?x:-x; }
il int read(){
    char c=getchar();int x=0,f=1;
    while(c<48) { if(c=='-')f=-1;c=getchar(); }
    while(c>47) x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x*f;
}const int maxn=5e3+5,maxm=5e4+5,inf=0x3f3f3f3f;

int n,m,S,T,dis[maxn],incf[maxn],pre[maxn],maxflow,ans;
bool vis[maxn];
int head[maxm<<1],t=1;
struct Edge{ int v,c,w;int next; };Edge e[maxm<<1];
il void add_edge(int u,int v,int c,int w){
    e[++t].v=v;e[t].c=c;e[t].w=w;e[t].next=head[u];head[u]=t;
    e[++t].v=u;e[t].c=0;e[t].w=-w;e[t].next=head[v];head[v]=t;
}

il bool SPFA(){
    std::queue<int> q;while(!q.empty()) q.pop();
    memset(dis,63,sizeof(dis));
    memset(vis,0,sizeof(vis));
    q.push(S);vis[S]=true;dis[S]=0;
    while(!q.empty()){
        int now=q.front();vis[now]=false;q.pop();
        for(rg i=head[now];i;i=e[i].next){
            int to=e[i].v;
            if(e[i].c && dis[to]>dis[now]+e[i].w){
                dis[to]=dis[now]+e[i].w;
                if(!vis[to])    q.push(to),vis[to]=true;
            }
        }
    }
    return dis[T]<inf;
}

int dfs(int now,int flow){
    if(now==T){ maxflow+=flow,ans+=dis[T]*flow;return flow; }
    vis[now]=true;
    int res=0,rest;
    for(rg i=head[now];i;i=e[i].next){
        int to=e[i].v;
        if(vis[to]) continue;
        if(e[i].c && dis[to]==dis[now]+e[i].w){
            rest=dfs(to,Min(e[i].c,flow));
            e[i].c-=rest;e[i^1].c+=rest;res+=rest;
            if(flow==res) break;    // 剪枝优化
        }
    }
    return res;
}

il void input(){
    n=read(),m=read(),S=read(),T=read();int u,v,c,w;
    for(rg i=1;i<=m;++i){
        u=read(),v=read(),c=read(),w=read();
        add_edge(u,v,c,w);
    }
}

int main(){
// freopen("zkw.in","r",stdin);
    input();
    while(SPFA())   dfs(S,inf);    
    printf("%d %d\n",maxflow,ans);
    return 0;
}
// Oh pick yourself up 'cause
// SPFA never die

例题：[SDOI2009] 晨跑

题目链接

折叠题干

[SDOI2009] 晨跑

题目描述

Elaxia 最近迷恋上了空手道，他为自己设定了一套健身计划，比如俯卧撑、仰卧起坐等等，不过到目前为止，他坚持下来的只有晨跑。

现在给出一张学校附近的地图，这张地图中包含 \(N\) 个十字路口和 \(M\) 条街道，Elaxia 只能从 一个十字路口跑向另外一个十字路口，街道之间只在十字路口处相交。

Elaxia 每天从寝室出发跑到学校，保证寝室编号为 \(1\)，学校编号为 \(N\)。

Elaxia 的晨跑计划是按周期（包含若干天）进行的，由于他不喜欢走重复的路线，所以在一个周期内，每天的晨跑路线都不会相交（在十字路口处），寝室和学校不算十字路口。

Elaxia 耐力不太好，他希望在一个周期内跑的路程尽量短，但是又希望训练周期包含的天数尽量长。

除了练空手道，Elaxia 其他时间都花在了学习和找 MM 上面，所有他想请你帮忙为他设计 一套满足他要求的晨跑计划。

存在 \(1\rightarrow n\) 的边存在。这种情况下，这条边只能走一次。

输入格式

第一行两个整数 \(N,M\)，表示十字路口数和街道数。

接下来 \(M\) 行，每行 \(3\) 个数 \(a,b,c\)，表示路口 \(a\) 和路口 \(b\) 之间有条长度为 \(c\) 的街道（单向）。

输出格式

一行两个整数，最长周期的天数和满足最长天数的条件下最短的路程度。

样例 #1

样例输入 #1

7 10
1 2 1
1 3 1
2 4 1
3 4 1
4 5 1
4 6 1
2 5 5
3 6 6
5 7 1
6 7 1

样例输出 #1

2 11

提示

  • 对于 \(30\%\) 的数据，\(N\le 20\)，\(M \le 120\)。
  • 对于 \(100\%\) 的数据，\(N\le 200\)，\(M\le 2\times 10^4\)。

这道题显然是费用流，因为每条边只希望走一次，那么这就是容量，而希望路程最小就是费用最小，故是最小费用最大流板子题。

发现题干中说“每天的晨跑路线都不会相交（在十字路口处）”，所以所谓的“每条边只走一次”题目中表达的含义其实是“每个点只走一次”。

如果我们要建立模型，这本来应该是边的属性，所以我们拆点，拆成一个入点一个出点，入点和出点之间的边容量为 \(1\)。

Miku's Code 
#include<bits/stdc++.h>
#define il inline
#define rg register int
#define cout std::cout
#define cerr std::cerr
#define push_back emplace_back
#define make_pair std::make_pair
#define endl '\n'
#define bits(x) std::bitset<x>
typedef long long ll;
typedef unsigned long long ull;
typedef double ff;
typedef long double llf;
typedef unsigned char byte;
typedef std::pair<int,int> PII;
const ff eps=1e-8;
int Max(int x,int y){ return x<y?y:x; }
int Min(int x,int y){ return x<y?x:y; }
int Abs(int x){ return x>0?x:-x; }
il int read(){
    char c=getchar();int x=0,f=1;
    while(c<48) { if(c=='-')f=-1;c=getchar(); }
    while(c>47) x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x*f;
}const int maxn=405,maxm=4e4+5,inf=0x3f3f3f3f;

int n,m,S,T,dis[maxn],incf[maxn],pre[maxn],maxflow,ans;
int head[maxm<<1],t=1;
bool vis[maxn];
struct Edge{ int v,c,w;int next; };Edge e[maxm<<1];
il void add_edge(int u,int v,int c,int w){
    e[++t].v=v;e[t].c=c;e[t].w=w;e[t].next=head[u];head[u]=t;
    e[++t].v=u;e[t].c=0;e[t].w=-w;e[t].next=head[v];head[v]=t;
}

il bool SPFA(){
    std::queue<int> q;while(!q.empty()) q.pop();
    for(rg i=0;i<=(n<<1);++i)    dis[i]=inf,vis[i]=false;
    dis[S]=0;vis[S]=true;q.push(S);incf[S]=inf;
    while(!q.empty()){
        int now=q.front();q.pop();vis[now]=false;
        for(rg i=head[now];i;i=e[i].next){
            int to=e[i].v;
            if(e[i].c && dis[to]>dis[now]+e[i].w){
                incf[to]=Min(incf[now],e[i].c);
                dis[to]=dis[now]+e[i].w;pre[to]=i;
                if(!vis[to])    q.push(to),vis[to]=true;
            }
        }
    }
    if(dis[T]==inf) return false;
    return true;
}

il void update(){
    int now=T;
    while(now!=S){
        int i=pre[now];
        e[i].c-=incf[T];
        e[i^1].c+=incf[T];
        now=e[i^1].v;
    }
    maxflow+=incf[T];ans+=dis[T]*incf[T];
}

il void input(){
    n=read(),m=read();S=1+n,T=n;int a,b,c;
    for(rg i=1;i<=n;++i)    add_edge(i,i+n,1,0);
    for(rg i=1;i<=m;++i){
        a=read(),b=read(),c=read();
        add_edge(a+n,b,1,c);
    }
}

int main(){
freopen("morningrun.in","r",stdin);
    input();
    while(SPFA())   update();
    printf("%d %d",maxflow,ans);
    return 0;
}
posted @ 2023-09-02 20:32  Sonnety  阅读(77)  评论(3)  编辑  收藏  举报