【学习笔记】【数学】【动态规划】概率与期望
还会持续性更新题目。
概率期望Sonnety都不做。
前言
Warning：本笔记含有大量 \(Latex\) 公式，可能会造成卡顿。
（反正我编辑的时候非常卡，只能放弃实时预览）
有问题请@我。
概率期望这个说到底和动态规划挂钩，逃离不了动态规划，而概率期望又给动态规划添了一层迷幻的色彩（指 \(double\) ）。
所以这篇博客应该重点不会在基础知识，可能后期会发展成杂题乱写的地步（？）
然后是我们的宣言：
基础知识（高中课本概率学基础）：
互斥事件：事件 \(A\) 和 \(B\) 的交集为空， \(A\) 与 \(B\) 就是互斥事件，也叫互不相容事件。 也可叙述为：不可能同时发生的事件。 如 \(A∩B\) 为不可能事件（ \(A\bigcap B=\varnothing\) ），那么称事件 \(A\) 与事件 \(B\) 互斥，其含义是：事件 \(A\) 与事件 \(B\) 在任何一次试验中不会同时发生。
对立事件：对立事件是指其中必有一个发生的两个互斥事件 。
独立事件：所谓独立事件就是某事件发生的概率与其它任何事件都无关，用集合的概念解释即集合之内所有事件发生的可能性范围互不相交。
概率
条件概率公式
定义：
条件概率：
在另外一个事件 \(B\) 已经发生的情况下，事件 \(A\) 发生的概率叫做 \(A\) 对 \(B\) 的条件概率。记作 \(p(A|B)\) ，易证\(p(AB)=p(A|B)p(B)\) ，若 \(p(A|B)==p(A)\) 则称事件 \(A\) 与事件 \(B\) 相互独立。
公式：
乘法公式：
由条件概率公式可得：
乘法公式的推广：
对于任何一个正整数 \(n>=2\) ，当 \(p(A_1A_2……A_{n-1})>0\) 时，有：
全概率公式
定义：
完备事件组：
若事件 \(A_1,A_2,……,A_n\) 满足：
-
\(A_i \bigcap A_j==\varnothing\)，\(i\neq j\)
-
\(A_1 \bigcup A_2 \bigcup A_3 \bigcup …… \bigcup A_n==\Omega\)
则称这些事件是完备事件组。
(也称事件组 \(A_1,A_2……A_n\) 是样本空间 \(\Omega\) 的一个划分)
公式：
设 \(B_1,B_2,……,B_n\)是样本空间 \(\Omega\) 的一个划分， \(A\) 是任一事件，则：
证明见图：
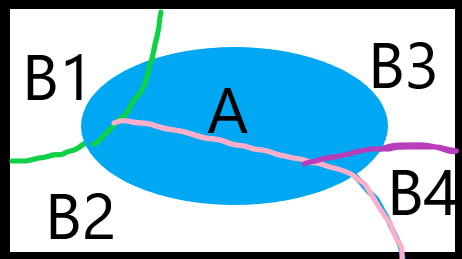
整个矩形为样本空间，蓝色椭圆是事件 \(A\).
显然 \(P(B_i)P(A|B_i)\) 等于 \(B_i\) 区域的那一块蓝色。
全概率公式将较难计算的事件 \(A\) 分割为多个小事件后相加。
老师的课件上是另一种理解方式：
例题：
某车间用甲、乙、丙三台机床进行生产，各台机床次品率分别为 \(0.05\) ，\(0.04\)，\(0.02\)，它们各自的产品分别占总量的\(0.25\)，\(0.35\)，\(0.40\)，将它们的产品混在一起，求任取一个产品是次品的概率。
解：
\(P(A)=0.25*0.05+0.04*0.35+0.02*0.40=0.0345\)
贝叶斯公式
定义
与全概率公式解决的问题恰好相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因。
返回上图：
贝叶斯公式要求的是大事件 \(A\) 已经发生的情况下，分割中小事件 \(B_i\) 的概率。
公式
设 \(B_1,B_2,……,B_n\)是样本空间 \(\Omega\) 的一个划分， \(A\) 是任一事件，则：
还是这张图：
我们先看分子： \(P(B_i)P(A|B_i)\) 毫无疑问是在 \(B_i\) 范围内事件 \(A\) 的概率。
而分母 \(\sum_{ j = 1 }^{ n }P(B_j)P(A|B_j)\) 则是事件 \(A\) 发生的概率。
例题：
仍然是上面的机床awa：
某车间用甲、乙、丙三台机床进行生产，各台机床次品率分别为 \(0.05\) ，\(0.04\)，\(0.02\)，它们各自的产品分别占总量的\(0.25\)，\(0.35\)，\(0.40\)，将它们的产品混在一起，取出的零件是次品，求它是第 \(i\) 台加工的概率。
0.0345
解：
甲：\(\frac{0.25*0.05}{0.05*0.25+0.04*0.35+0.02*0.40}\) 约等于 \(0.362\)
乙和丙大家自己算吧算完了发评论区（骗个评论）检查你是否真正掌握。
期望
定义：
期望是某件事情大量发生的平均结果。
例如：洛天依和乐正绫玩游戏，现在手里有十三张牌，分别是： \(6\) 张“不更新声库的C社”卡， \(6\) 张“稔无可稔”卡， \(1\) 张“老板跑路的五维”卡，如果你抽到了“老板跑路的五维”卡，那么乐正绫给洛天依买 \(10\) 个包子，否则洛天依要给乐正绫买 \(1\) 个包子。
在一定区间内变量取值为无限个，或者数值可以一一列举出来的变量叫离散性随机变量。
一个离散型随机变量的数学期望是实验中每次可能的结果乘以其结果概率的总和。
返回上面的例子，有:
\(\frac {(-1)*(13-1)}{13}+\frac {(10)*(1)}{13}=-\frac{2}{13}\)
可见我们的洛天依小姐（除非运气爆棚）大概率是会赔。
公式：
设 \(A\) 是一个离散的随机变量，输出值为 \(a_1,a_2,……,a_n\)，与其相应的概率分别为 \(p_1,p_2,……,p_n\) （\(\sum_{i=1}^{n}p_i=1\)) ，得期望值：
期望的线性性质：
假设随机变量 \(X\) 和 \(Y\) 在同一样本空间中， \(X+Y\) 是定义在此样本空间上的随机函数，有：
对于第一个公式，很好说设随机变量 \(X=x_1+x_2+x_3\) ，对于任意的 \(\omega \in \Omega\)，存在：
\(X(\omega) = x_1(\omega) + x_2(\omega) + x_3(\omega)\)
对于第二个公式，只有在 \(X_1\) 与 \(X_2\) 相互独立时成立。
例题：
给出一个 \(6\) 面骰子，掷骰子 \(2\) 次，求期望总和。
按照概率的做法，就是将所有的情况枚举，乘上概率，最后相加，共 \(36\) 种情况，很麻烦。
使用期望，我们设 \(X\) 是投掷两次骰子的和， \(x_1\) 是投掷第一次的和， \(x_2\) 是投掷第二次的和。
可得：
\(X=x_1+x_2\)
\(E(X)=E(x_1)+E(x_2)\)
知道 \(x_1\) 与 \(x_2\) 相互独立，且 \(E(x_1)=E(x_2)\) 考虑只求 \(E(x_1)\)。
\(E(x_1)=\frac{1}{6}+\frac{2}{6}+\frac{3}{6}+\frac{4}{6}+\frac{5}{6}+\frac{6}{6}=3.5\)
可得 \(E(X)=7\) 。
全期望公式：
参考资料：
《浅析竞赛中一类数学期望问题的解决方法》2009 - 汤可因
为什么要看这么多？因为我也不会，大家最好看别人的看会了，不要看我这个垃姬博客（
Warning：不保证理解和证明正确，以下证明可能误导您的思路，慎看
呃呃，这个东西吧咱可以感性理解。
（主要是很多人也没有提这个公式，但是很多题又用了这个公式，这个公式本身含义感性理解不难，但是放到纸面上就较难理解。）
给定一个类似于条件概率的问题：假如事件 \(A\) 一定发生，那么样本空间 \(\Omega\) 的随机变量 \(X\) 会发生什么变化？
我们记这个受约束的随机变量为 \(X|A\) ，那么对于 \(\forall x \in X(\Omega)\)，有：
又被写成：
（或许我们可以感性理解这个公式）
接下来我们来证明这个式子。
（非常认真的吐槽一下，就是咱这个 \(E[X|Y=y]\) 能不能稍微解释一下，我看了这么多篇文让我以为 \(y=X|Y\) 是一个随机事件，但是事实上这里说的是 \(Y==y\)）
证明：
首先说 \(E[X | Y]\) ， \(X|Y\) 它是一个新的随机变量，其期望为：
解释一下，就是 \(X|Y\) 的期望等于在 \(Y\) 这个事件里抽取一个事件 \(y\) 的概率乘上在 \(y\) 这个事件内部的 \(X\) 的期望。
而这个内层的 \(E[ ]\) 代表的是这 \(y\) 一小块里的 \(x\) 的期望，下图的天蓝色部分。
举个例子，我们构想一个随机变量 \(X(\Omega)\) 表示每个人上次考试考的成绩， \(Y(\Omega)\) 表示每个人所属于的班级，那么 \(E[X|(Y==y)]\) 就表示每个班取一个人的成绩的期望值，取和，就是我们整个学校抽取一个人的成绩期望。
还是那句话，解释不负责任，都是猜测
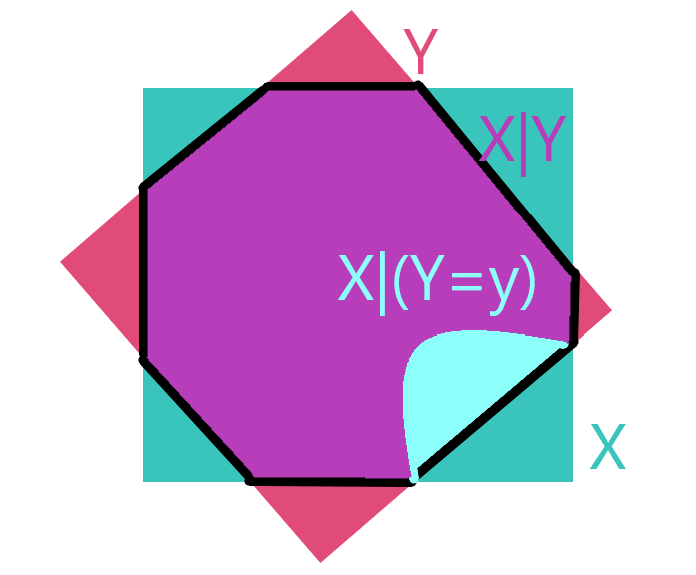
\(Y(\Omega)\) 是一个随机事件，它是随机的班级， \(X(\Omega)\) 是每个人上次考试考的成绩， \(X|Y\) 中的 \(Y\) 并不是一个确定的班级，仍然是个随机变量。
但是在 \(X|(Y==y)\) 中，我们的 \(Y\) 这里就成了一个固定的班级就是这个人的班级，所以该期望是图中的天蓝色小块，很多天蓝色小块相加便是其期望。
因此外面在套一层 \(E[ ]\) 的含义是将 \(y\) 变成 \(Y\) 。
（当然这个图可能有一点不对，你就当有一部分人没有考试，有一部分人没有班级（？））
然后好像有一个叫迭代期望公式的东西也可以解释它为什么外面还能套一个\(E[ ]\)
\(Rolling\)_\(star\) 老师给了我一个我觉得非常可信的解释：里面的 \(E[ ]\) 是针对 \(Y\) 的分布得到的期望，而外面的 \(E[ ]\) 则是针对 \(X\) 的。
定理证明如下：
学这个有什么用？
还是说回我们的班级问题，我们构想一个随机变量 \(X(\Omega)\) 表示每个人上次考试考的成绩， \(Y(\Omega)\) 表示每个人所属于的班级，有 \(E[X]=E[E[X|Y]]=E[X|Y=y]P(Y=y)\)，其中\(E[X|Y==y]\) 就表示每个班取一个人的成绩的期望值，根据此公式，我们只要算出每个班级的平均成绩然后加权平均即可。
很多题目都应用了这个公式，比如说 \(osu\) ，比如说 \(Easy\) ，比如说 列队春游 ，只要有求期望且问题具有概率性的，或者大问题可以分割为小问题再加和的，都可以应用这个公式。
据说这个公式还有其他形式，但是我不会，长大再学。
(upd:2023/7/24)
今天再次讨论了本公式和期望逆推问题。
以[SCOI2008] 奖励关为例。
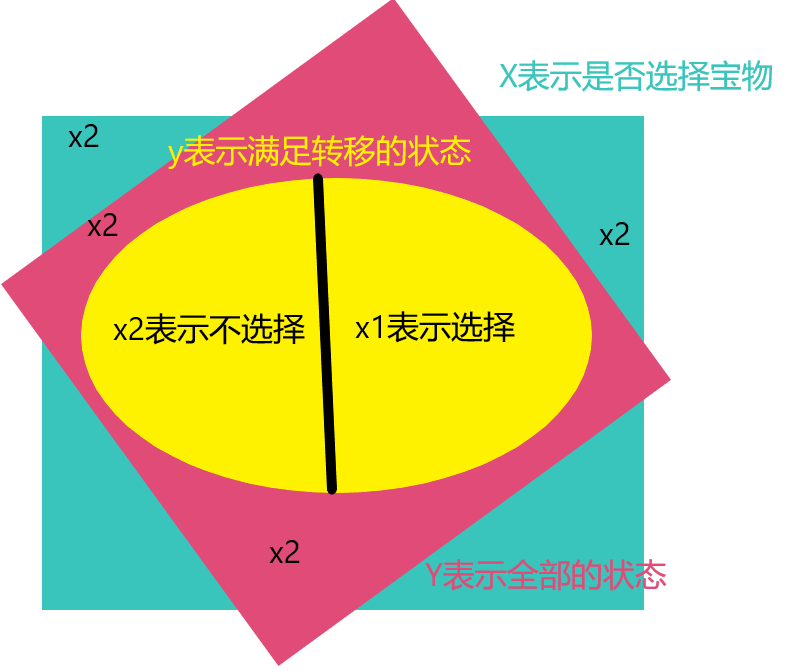
如图，图中：满足转移的状态指可以选择宝物的状态。
根据本公式 \(E[X]=E[E[X|Y]]\) 可得：
\(E[X]=\sum_\limits{x \in X(\Omega)} \sum_\limits{y \in Y(\Omega)} x p(X=x | Y=y) p(Y=y)\)
我们发现 \(p(X=x |Y=y)\) 是带有条件的，可以先给他拆开：
\(E[X]=x_1 \times p(x_1|y_1)p(y_1) +x_1 \times p(x_1|y_2) p(y_2)+x_2 \times p(x_2 | y_1) p(y_1)+x_2 \times p(x_2|y_2)p(y_2)\)
这个式子我们发现，\(x_1\) 表示选择在不满足选择的条件下概率为 \(0\) ，即 \(p(x_1|y_2)=0\)。
\(E[X]=x_1 \times p(x_1|y_1)p(y_1) \times p(x_2 | y_1) p(y_1)+x_2 \times p(x_2|y_2)p(y_2)\)
本式子，倒推的过程中，将 \(x \times p(x|y)\) 类似的式子捆绑，然后再乘其概率，先满足其概率条件，再乘上条件的概率。
正推的过程则是先乘上概率再进行下一步的。
倒推从结果开始，全事件概率为 \(1\)。
正推可能会造成全事件概率 \(1\) 的缺失或增大。
不是有的题可以倒推，而是有的题可以正推。
总之，如果遇到遇到当前状态与下一状态并不相互独立的情况，我们应该考虑倒推。
当然我们的 \(CCComfy\) 老师也为我提供了一个思路：
蓝色点乘其期望+粉色点乘其期望=黑色点乘其期望。
(upd：2023/7/24日晚）
重新复习了绿豆蛙的归宿，感觉正推和逆推都是可以的，只是看谁的实现更方便，谁的边界更明显。
这里更新一下绿豆蛙的正推逆推两种做法与详解：
正推：\(f_v=\frac{f_u+w_{u,v}*p_v}{du}\)
这里的 \(p_v\) 表示的是起点到点 \(v\) 的概率，显然其概率并不等于 \(1\)，因为它不一定会到达这个点。
逆推：\(f_u=\frac{f_v+w_{u,v}}{du}\)
这里其实隐藏了一个 \(p_u\) 表示起点 \(u\) 到达终点的概率，其条件概率和一定为 \(1\) ，因为题目要求必须到达终点。
例题：
学习唱一首新歌由洛天依完成平均需要 \(4\) 小时，而乐正绫有 \(0.4\) 的概率来帮忙，两个人互相成就练习新歌只需要 \(3\) 个小时。
求洛天依学会一首新歌的期望。
解：
设随机事件 \(X\) 是完成该工作的人数，而 \(Y\) 表示完成工作的期望时间。
\(E[Y]=E(Y|(X=1))*P(X=1)+E(Y|(X=2))*P(X=2)=3.6\)
杂题乱写(?)
我将在这里积累做题方法：
-
对于很多的动态转移方程，我们可以选择考虑一下滚动数组。
-
如果遇到当前状态与下一状态并不相互独立的情况，我们应该考虑倒推（Red is good/卡牌游戏）。
-
正难则反。（矩阵粉刷）
-
或许可以对一些确定或者半确定的概率进行预处理（聪聪和可可）
-
当贡献等于 \(1\) 时，可以将期望转换为概率。
[国家集训队] 单选错位
[国家集训队] 单选错位
题目描述
gx 和 lc 去参加 noip 初赛，其中有一种题型叫单项选择题，顾名思义，只有一个选项是正确答案。
试卷上共有 \(n\) 道单选题，第 \(i\) 道单选题有 \(a_i\) 个选项，这 \(a_i\) 个选项编号是 \(1,2,3,\ldots,a_i\)，每个选项成为正确答案的概率都是相等的。
lc 采取的策略是每道题目随机写上 \(1 \sim a_i\) 的某个数作为答案选项，他用不了多少时间就能期望做对 \(\sum_{i=1}^n \frac{1}{a_i}\) 道题目。gx 则是认认真真地做完了这 \(n\) 道题目，可是等他做完的时候时间也所剩无几了，于是他匆忙地把答案抄到答题纸上，没想到抄错位了：第 \(i\) 道题目的答案抄到了答题纸上的第 \(i+1\) 道题目的位置上，特别地，第 \(n\) 道题目的答案抄到了第 \(1\) 道题目的位置上。
现在 gx 已经走出考场没法改了，不过他还是想知道自己期望能做对几道题目，这样他就知道会不会被 lc 鄙视了。
我们假设 gx 没有做错任何题目，只是答案抄错位置了。
输入格式
\(n\) 很大，为了避免读入耗时太多，输入文件只有 \(5\) 个整数参数 \(n, A, B, C, a_1\)，由上交的程序产生数列 \(a\)。下面给出 pascal/C/C++ 的读入语句和产生序列的语句（默认从标准输入读入）：
// for pascal
readln(n,A,B,C,q[1]);
for i:=2 to n do
q[i] := (int64(q[i-1]) * A + B) mod 100000001;
for i:=1 to n do
q[i] := q[i] mod C + 1;
// for C/C++
scanf("%d%d%d%d%d", &n, &A, &B, &C, a + 1);
for (int i = 2; i <= n; i++)
a[i] = ((long long) a[i - 1] * A + B) % 100000001;
for (int i = 1; i <= n; i++)
a[i] = a[i] % C + 1;
选手可以通过以上的程序语句得到 \(n\) 和数列 \(a\)（\(a\) 的元素类型是 \(32\) 位整数），\(n\) 和 \(a\) 的含义见题目描述。
输出格式
输出一个实数，表示 gx 期望做对的题目个数，保留三位小数。
样例 #1
样例输入 #1
3 2 0 4 1
样例输出 #1
1.167
提示
【样例说明】
| 正确答案 | gx的答案 | 做对题目 | 出现概率 |
|---|---|---|---|
| \(\{1,1,1\}\) | \(\{1,1,1\}\) | \(3\) | \(\frac16\) |
| \(\{1,2,1\}\) | $ {1,1,2}$ | \(1\) | \(\frac16\) |
| \(\{1,3,1\}\) | $ {1,1,3} $ | \(1\) | \(\frac16\) |
| \(\{2,1,1\}\) | $ {1,2,1} $ | \(1\) | \(\frac16\) |
| \(\{2,2,1\}\) | $ {1,2,2}$ | \(1\) | \(\frac16\) |
| \(\{2,3,1\}\) | ${1,2,3} $ | \(0\) | \(\frac16\) |
\(a = \{2,3,1\}\)。
共有 \(6\) 种情况，每种情况出现的概率是 \(\frac{1}{6}\)，gx 期望做对 \(\frac{3+1+1+1+1+0}6 = \frac76\) 题。（相比之下，lc 随机就能期望做对 \(\frac{11}6\) 题）
对于 \(30\%\) 的数据，\(n\leq 10, C\leq 10\)。
对于 \(80\%\) 的数据，\(n\leq 10^4, C\leq 10\)。
对于 \(90\%\) 的数据，\(n\leq 5\times 10^5, C\leq 10^8\)。
对于 \(100\%\) 的数据，\(2\leq n\leq 10^7, 0\leq A,B,C \leq 10^8\)，\(1 \leq a_i \leq 10^8\)。
解题：
非常基础的一道题目，我们设第 \(i\) 道题目的答案是已知的， 那么如果两道题的选项数量相同第 \(i+1\) 道题目的答案与第 \(i\) 道题目相同的可能是 \(\frac{1}{a_i}\)，如果两道题选项数量不同根据条件概率公式我们可以先让两道题的选项数量相同，可能为 \(\frac{min(a_i,a_{i+1})}{max(a_i,a{i+1}}\) ,再乘上 \(\frac{1}{min(a_i,a_{i+1})}\) 。
Miku's Code
#include<bits/stdc++.h>
using namespace std;
typedef long long intx;
const int maxn=1e7+50;
int n,A,B,C;
intx a[maxn];
double ans;
void input(){
scanf("%d %d %d %d %d",&n,&A,&B,&C,a+1);
for(int i=2;i<=n;++i){
a[i]=((intx)a[i-1]*A+B)%100000001;
}
for(int i=1;i<=n;++i){
a[i]=a[i]%C+1;
}
a[n+1]=a[1];
}
int main(){
input();
for(int i=1;i<=n;++i){
ans+=(double)(1)/max(a[i],a[i+1]);
}
printf("%.3lf\n",ans);
return 0;
}
绿豆蛙的归宿
绿豆蛙的归宿
题目背景
随着新版百度空间的上线，Blog 宠物绿豆蛙完成了它的使命，去寻找它新的归宿。
题目描述
给出张 \(n\) 个点 \(m\) 条边的有向无环图，起点为 \(1\)，终点为 \(n\)，每条边都有一个长度，并且从起点出发能够到达所有的点，所有的点也都能够到达终点。
绿豆蛙从起点出发，走向终点。 到达每一个顶点时，如果该节点有 \(k\) 条出边，绿豆蛙可以选择任意一条边离开该点，并且走向每条边的概率为 \(\frac{1}{k}\) 。现在绿豆蛙想知道，从起点走到终点的所经过的路径总长度期望是多少？
输入格式
输入的第一行是两个整数，分别代表图的点数 \(n\) 和边数 \(m\)。
第 \(2\) 到第 \((m + 1)\) 行，每行有三个整数 \(u, v, w\)，代表存在一条从 \(u\) 指向 \(v\) 长度为 \(w\) 的有向边。
输出格式
输出一行一个实数代表答案，四舍五入保留两位小数。
样例 #1
样例输入 #1
4 4
1 2 1
1 3 2
2 3 3
3 4 4
样例输出 #1
7.00
提示
数据规模与约定
- 对于 \(20\%\) 的数据，保证 \(n \leq 10^2\)。
- 对于 \(40\%\) 的数据，保证 \(n \leq 10^3\)。
- 对于 \(60\%\) 的数据，保证 \(n \leq 10^4\)。
- 对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 10^5\)，\(1 \leq m \leq 2 \times n\)，\(1 \leq u, v \leq n\)，\(1 \leq w \leq 10^9\)，给出的图无重边和自环。
解题：
（ps:DFS批，简称DP）
同样基础。
呃呃链式前向星建边存边然后 \(dfs\) 一遍，回溯的时候倒推更新动态转移，初始化 \(f_n=0\)，动态转移方程：
然后这道题需要注意一下判断点有没有走过，因为可能会有交点(比如说样例里的点 \(3\) )，那你肯定不能让他加两次点 \(4\) 。
（upd：在探究逆推问题时提到了本题，并分析了顺推逆推两种做法，详见全期望公式证明。）
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+50,maxm=2e5+50;
int n,m,d[maxn];
double f[maxn];
bool vis[maxn];
int head[maxm],t;
struct edge{
int u,v,w;
int next_;
};edge e[maxm];
void add_edge(int u,int v,int w){
e[++t].u=u;
e[t].v=v;
e[t].w=w;
e[t].next_=head[u];
head[u]=t;
}
void dfs(int now,int fa){
if(vis[now]==true) return;
vis[now]=true;
for(int i=head[now];i;i=e[i].next_){
int to=e[i].v,val=e[i].w,du=d[now];
dfs(to,now);
f[now]=f[now]+(double)(f[to]+(double)val)/du;
}
}
void input(){
int u,v,w;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d %d %d",&u,&v,&w);
++d[u];
add_edge(u,v,w);
}
f[n]=0;
}
int main(){
input();
dfs(1,0);
printf("%.2lf\n",f[1]);
return 0;
}
POJ3071 Football
题目描述
\(2^n\) 个队伍参加一场单淘汰制足球锦标赛，它们被编号为 \(1,2,…,2^n\) 。每一轮比赛，未被淘汰的队伍按照升序被放在一个列表里，接下来，列表里的第 \(1\) 个队伍跟第 \(2\) 个队伍比赛，第 \(3\) 个队伍跟第 \(4\) 个队伍比赛，等等。获胜的队伍晋级下一轮，战败的队伍被淘汰。\(n\) 轮之后，只有一个队伍留下来，那个队伍就是冠军。
有一个矩阵 \(1,2,…,2^n\)，\(p_{i,j}\) 表示队伍 \(i\) 在一场比赛中战胜队伍 \(j\) 的概率，决定了哪支队伍更容易赢得冠军。
输入格式
多组测试点。每个测试点都由一个 \(n(1\leqslant{n}\leqslant{7})\) 开头，接下来的 \(2^n\) 行每行有 \(2^n\) 个值， \(i\) 行的第 \(j\) 个值是 \(p_{i,j}\) 。矩阵 \(P\) 满足对任意的 \(i\neq{j}\) , \(p_{ij}=1-p_{ji}\) ，并且对任意 \(i\)，\(p_{i_i}\)等于0.
输入结束的标志是一个数字 \(-1\)。
矩阵 \(P\) 中的所有数据都以小数给出，为避免精度问题，请使用 \(double\) 数据类型作答。
输出格式
对每个测试点输出一行整数，表示哪个队伍最有可能成为冠军。为了避免精度问题，数据保证任意两个队伍之间成为冠军的概率之差不小于 \(0.01\)。
样例
输入
2
0.0 0.1 0.2 0.3
0.9 0.0 0.4 0.5
0.8 0.6 0.0 0.6
0.7 0.5 0.4 0.0
-1
输出
2
样例解释：
在样例中，第一轮队伍 \(1\) 对阵队伍 \(2\) ，队伍 \(3\) 对阵队伍 \(4\) 。两场比赛的胜者在第二轮对阵来决出冠军。队伍\(2\)获得冠军的概率如下：
队伍 \(3\) 的获胜概率紧随其后，为 \(0.372\) 。
解题：
很明显的概率dp题目。
（但是老师不讲我肯定不会）
设 \(f_{i,j}\) 表示队伍 \(j\) 在第 \(i\) 轮晋级的概率。
初始化：\(f_{0,j}=1\)。
得转移方程：
但是这个题的难点不在于推一个转移方程，而是如何确定队伍 \(j\) 在每一轮遇到的对手都有一个范围。
比如说我们发现，第一轮里队伍 \(1\) 与队伍 \(2\) 对决决出一个胜者，第二轮显然是 \(1\) 与 \(2\) 中胜者与 \(3\) 与 \(4\) 之间胜者决出胜者。
因此我们总结出规律：决出胜者就像合并一样，队伍 \(j\) 在第 \(i\) 轮只能与在第 \(i\) 轮和它一组且在第 \(i-1\) 轮不在一组的队伍对决，可得队伍 \(i\) 在 第\(j\) 轮中遇到的队伍 \(k\)必须满足的条件：
（ps:\(\bigwedge\)的意思是并列）
于是有代码：
Miku's Code
#include<iostream>
#include<stdio.h>
//因为是poj的题所以没有万能头
using namespace std;
const int maxn = (1<<8)+2;
int n,nlen;
double p[maxn][maxn],f[maxn][maxn];
void input(){
nlen=(1<<n);
for(int i=0;i<nlen;++i){
for(int j=0;j<nlen;++j){
scanf("%lf",&p[i][j]);
}
f[0][i]=(double)1.0;
}
}
void work(){
for(int i=1;i<=n;++i){
for(int j=0;j<nlen;++j){
f[i][j]=(double)0.0;
//不要忘记
for(int k=0;k<nlen;++k){
if(j==k) continue;
if(j/(1<<(i-1))!=k/(1<<(i-1)) && j/(1<<i)==k/(1<<i))
f[i][j]+=f[i-1][j]*f[i-1][k]*p[j][k];
}
}
}
}
int main(){
while(scanf("%d",&n) && n!=-1){
input();
work();
int ans=0;
for(int i=1;i<nlen;i++){ //遍历每一个队伍
if(f[n][ans]<f[n][i]) ans=i;
}
printf("%d\n",ans+1); //我们的队伍编号是从0开始的
}
return 0;
}
[NOI2005] 聪聪与可可
[NOI2005] 聪聪与可可
题目描述
在一个魔法森林里，住着一只聪明的小猫聪聪和一只可爱的小老鼠可可。虽 然灰姑娘非常喜欢她们俩，但是，聪聪终究是一只猫，而可可终究是一只老鼠， 同样不变的是，聪聪成天想着要吃掉可可。
一天，聪聪意外得到了一台非常有用的机器，据说是叫 GPS，对可可能准确 的定位。有了这台机器，聪聪要吃可可就易如反掌了。于是，聪聪准备马上出发， 去找可可。而可怜的可可还不知道大难即将临头，仍在森林里无忧无虑的玩耍。 小兔子乖乖听到这件事，马上向灰姑娘报告。灰姑娘决定尽快阻止聪聪，拯救可 可，可她不知道还有没有足够的时间。
整个森林可以认为是一个无向图，图中有 \(N\) 个美丽的景点，景点从 \(1\) 至 \(N\) 编号。小动物们都只在景点休息、玩耍。在景点之间有一些路连接。
当聪聪得到 GPS 时，可可正在景点 \(M\)(\(M≤N\))处。以后的每个时间单位，可可 都会选择去相邻的景点(可能有多个)中的一个或停留在原景点不动。而去这些地方所发生的概率是相等的。假设有 \(P\) 个景点与景点 M 相邻，它们分别是景点 R、 景点 S，……景点 Q，在时刻 \(T\) 可可处在景点 M，则在( $ T+1 $ )时刻，可可有 \(1/(1 +P)\) 的可能在景点 R，有 \(1/(1 +P)\) 的可能在景点 S，……，有 \(1/(1 +P)\) 的可能在景点 Q，还有\(1/(1 +P)\)的可能停在景点 M。
我们知道，聪聪是很聪明的，所以，当她在景点 C 时，她会选一个更靠近 可可的景点，如果这样的景点有多个，她会选一个标号最小的景点。由于聪聪太 想吃掉可可了，如果走完第一步以后仍然没吃到可可，她还可以在本段时间内再 向可可走近一步。
在每个时间单位，假设聪聪先走，可可后走。在某一时刻，若聪聪和可可位 于同一个景点，则可怜的可可就被吃掉了。
灰姑娘想知道，平均情况下，聪聪几步就可能吃到可可。而你需要帮助灰姑 娘尽快的找到答案。
输入格式
数据的第 1 行为两个整数 \(N\) 和 \(E\)，以空格分隔，分别表示森林中的景点数和 连接相邻景点的路的条数。
第 2 行包含两个整数 \(C\) 和 \(M\)，以空格分隔，分别表示初始时聪聪和可可所在的景点的编号。
接下来 E 行，每行两个整数，第 \(i+2\) 行的两个整数 \(A_i\)和 \(B_i\)表示景点 \(A_i\)和景点 \(B_i\) 之间有一条路。 所有的路都是无向的，即：如果能从 A 走到 B，就可以从 B 走到 A。
输入保证任何两个景点之间不会有多于一条路直接相连，且聪聪和可可之间必有路直接或间接的相连。
输出格式
输出 1 个实数，四舍五入保留三位小数，表示平均多少个时间单位后聪聪会把可可吃掉。
样例 #1
样例输入 #1
4 3
1 4
1 2
2 3
3 4
样例输出 #1
1.500
样例 #2
样例输入 #2
9 9
9 3
1 2
2 3
3 4
4 5
3 6
4 6
4 7
7 8
8 9
样例输出 #2
2.167
提示
【样例说明 1】
开始时，聪聪和可可分别在景点 1 和景点 4。
第一个时刻，聪聪先走，她向更靠近可可(景点 4)的景点走动，走到景点 2， 然后走到景点 3；假定忽略走路所花时间。
可可后走，有两种可能： 第一种是走到景点 3，这样聪聪和可可到达同一个景点，可可被吃掉，步数为 \(1\)，概率为\(0.5\)。
第二种是停在景点 4，不被吃掉。概率为 \(0.5\)。
到第二个时刻，聪聪向更靠近可可(景点 4)的景点走动，只需要走一步即和 可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。 所以平均的步数是 \(1\times 1/2 + 2\times 1/2 =1.5\) 步。
【样例说明 2】
森林如下图所示：
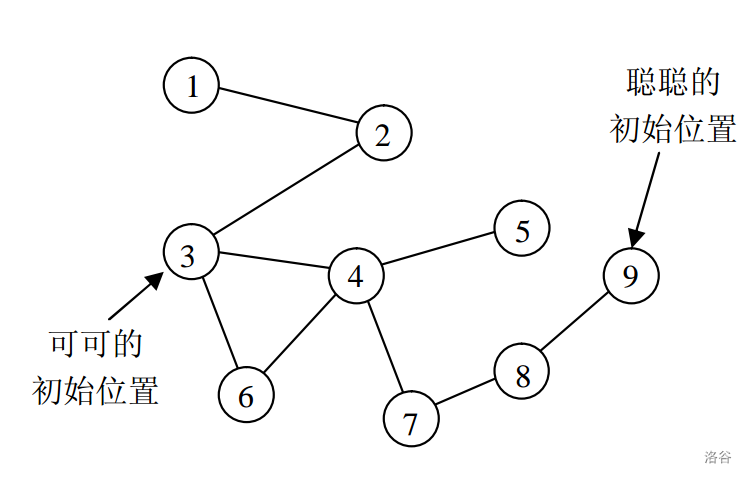
对于 50%的数据，\(1≤N≤50\)。
对于所有的数据，\(1≤N,E≤1000\)。
解题：
好，和前面的题目都不能一概而论，不愧是我们的国赛题。
首先就是我们发现聪聪走的路是跟着可可的，我们可以枚举可可的每一种位置可能，那么聪聪的路显然是固定的，可以通过 \(BFS\) 预处理出。
然后就是通过记忆化搜索实现的动态规划，注意我们小猫咪可以走两步，设 \(f_{i_j}\) 表示聪聪在 \(i\) 点,可可在 \(j\) 点时,聪聪抓到可可的期望， \(step_{i,j}\) 表示聪在 \(i\) 点,可可在 \(j\) 点时,聪聪下一步的行动， \(d_j\) 表示 \(j\) 点入度，方程：
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=55,maxe=1050;
int n,E,C,M;
int d[maxe],dis[maxe][maxe],step[maxe][maxe];
bool vis[maxe];
double f[maxe][maxe];
/*
变量声明：
d表示点入度
dis表示两点间距离,用BFS预处理出
step[i][j]表示聪聪在i点,可可在j点时,聪聪下一步的行动
f[i][j]表示聪聪在i点,可可在j点时,聪聪抓到可可的期望
*/
int head[maxe<<1],t;
struct edge{
int u,v;
int next_;
};edge e[maxe<<1];
void add_edge(int u,int v){
e[++t].u=u;
e[t].v=v;
e[t].next_=head[u];
head[u]=t;
}
void input(){
int u,v;
scanf("%d %d",&n,&E);
scanf("%d %d",&C,&M);
for(int i=1;i<=E;++i){
scanf("%d %d",&u,&v);
add_edge(u,v);
add_edge(v,u);
++d[u],++d[v];
}
for(int i=0;i<=n;++i){
for(int j=0;j<=n;++j){
f[i][j]=-1.0;
}
}
}
void BFS(){
memset(dis,-1,sizeof(dis));
for(int i=1;i<=n;++i){
queue<int> q;
while(!q.empty()){
q.pop();
}
q.push(i);
dis[i][i]=0;
while(!q.empty()){
int tp=q.front();
q.pop();
for(int j=head[tp];j;j=e[j].next_){
int to=e[j].v;
if(dis[i][to]==-1){
dis[i][to]=dis[i][tp]+1;
q.push(to);
}
}
}
}
}
void select(){
memset(step,0x7f,sizeof(step));
for(int i=1;i<=n;++i){
for(int j=head[i];j;j=e[j].next_){
int to=e[j].v;
for(int k=1;k<=n;++k){
if(dis[i][k]==dis[to][k]+1 && step[i][k]>to){
step[i][k]=to;
}
}
}
}
}
double work(int i,int j){
if(f[i][j]!=-1.0) return f[i][j]; //算过了就不再算了
if(i==j) return f[i][j]=0.0;
if(step[i][j]==j) return f[i][j]=1.0;
if(step[step[i][j]][j]==j) return f[i][j]=1.0;
//我们小猫咪是可以走两步的捏,这就是我们小猫咪的力量!!!
f[i][j]=0.0;
for(int k=head[j];k;k=e[k].next_){
f[i][j]+=work(step[step[i][j]][j],e[k].v);
}
f[i][j]=(f[i][j]+work(step[step[i][j]][j],j))/(double)(d[j]+1) +1.0;
return f[i][j];
}
int main(){
input();
BFS(); //BFS预处理图中所有点的距离
select(); //选择较近的或编号较小的
//for(int i=1;i<=n;++i){
// for(int j=1;j<=n;++j){
// cout<<dis[i][j]<<"---"<<step[i][j]<<' ';
// }
// cout<<endl;
//}
printf("%.3lf\n",work(C,M));
return 0;
}
WJMZBMR打osu! / Easy
WJMZBMR打osu! / Easy
题目背景
原 维护队列 参见 P1903
题目描述
某一天WJMZBMR在打osu~~~但是他太弱逼了，有些地方完全靠运气:(
我们来简化一下这个游戏的规则
有 \(n\) 次点击要做，成功了就是 o，失败了就是 x，分数是按 combo 计算的，连续 \(a\) 个 combo 就有 \(a\times a\) 分，combo 就是极大的连续 o。
比如ooxxxxooooxxx，分数就是 \(2 \times 2 + 4 \times 4 = 4 +16=20\)。
Sevenkplus 闲的慌就看他打了一盘，有些地方跟运气无关要么是 o 要么是 x，有些地方 o 或者 x 各有 \(50\%\) 的可能性，用 ? 号来表示。
比如 oo?xx 就是一个可能的输入。
那么 WJMZBMR 这场 osu 的期望得分是多少呢？
比如 oo?xx 的话，? 是 o 的话就是 oooxx（\(9\)），是x的话就是 ooxxx（\(4\)），期望自然就是 \((4+9)/2 =6.5\) 了。
输入格式
第一行一个整数 \(n\)（\(n\le3\times10^5\)），表示点击的个数
接下来一个字符串，每个字符都是 o，x，? 中的一个
输出格式
一行一个浮点数表示答案
四舍五入到小数点后 \(4\) 位
如果害怕精度跪建议用 long double 或者 extended。
样例 #1
样例输入 #1
4
????
样例输出 #1
4.1250
解题：
这道题太有意思了。
滚动数组之后是我做过的内存最小的蓝题（
Miku's Code
#include<bits/stdc++.h>
using namespace std;
int n,cur;
char s;
double f[2],g[2];
void work(){
for(int i=1;i<=n;++i){
scanf("%c",&s);
cur=cur^1;
f[cur]=0;
g[cur]=0;
if(s=='x'){
f[cur]=f[cur^1];
g[cur]=0;
}
else if(s=='o'){
f[cur]=f[cur^1]+2*g[cur^1]+1;
g[cur]=g[cur^1]+1;
}
else{
f[cur]=f[cur^1]+g[cur^1]+0.5;
g[cur]=g[cur^1]/2+0.5;
}
}
}
int main(){
scanf("%d",&n);
getchar();
work();
printf("%.4lf\n",f[cur]);
}
OSU!
OSU!
题目背景
原 《产品排序》 参见P2577
题目描述
osu 是一款群众喜闻乐见的休闲软件。
我们可以把 osu 的规则简化与改编成以下的样子:
一共有 \(n\) 次操作，每次操作只有成功与失败之分，成功对应 \(1\)，失败对应 \(0\)，\(n\) 次操作对应为 \(1\) 个长度为 \(n\) 的 01 串。在这个串中连续的 \(X\) 个 \(1\) 可以贡献 \(X^3\) 的分数，这 \(x\) 个 \(1\) 不能被其他连续的 \(1\) 所包含（也就是极长的一串 \(1\)，具体见样例解释）
现在给出 \(n\)，以及每个操作的成功率，请你输出期望分数，输出四舍五入后保留 \(1\) 位小数。
输入格式
第一行有一个正整数 \(n\)，表示操作个数。接下去 \(n\) 行每行有一个 \([0,1]\) 之间的实数，表示每个操作的成功率。
输出格式
只有一个实数，表示答案。答案四舍五入后保留 \(1\) 位小数。
样例 #1
样例输入 #1
3
0.5
0.5
0.5
样例输出 #1
6.0
提示
【样例说明】
\(000\) 分数为 \(0\)，\(001\) 分数为 \(1\)，\(010\) 分数为 \(1\)，\(100\) 分数为 \(1\)，\(101\) 分数为 \(2\)，\(110\) 分数为 \(8\)，\(011\) 分数为 \(8\)，\(111\) 分数为 \(27\)，总和为 \(48\)，期望为 \(\dfrac{48}8 = 6.0\)。
\(n \leq 1 \times 10 ^ 5\)。
解题：
似曾相识燕归来(?)
长得一摸一样，就是全都当成上一题的'\(?\)'处理就行，设 \(f_i\) 表示到第 \(i\) 位的期望。
根据完全立方公式得 \((n+1)^3-n^3=3n^2+3n+1\) ，我们需要维护两个期望，设 \(f1_i\) 表示到 第 \(i\) 位的 \(n\) 的期望， \(f2_i\) 表示到第 \(i\) 位的 \(n^2\) 的期望。
- 假设 \(i==1\) ， \(f1_i=f_{i-1}+1\) ，\(f2_i=f2_{i-1}+f_1{i-1}*2+1\) ， \(g_i=g_{i-1}+1\) 。
- 假设 \(i==0\) ，\(f1_i=f_{i-1}\) ， \(f2_i=f2_{i-1}\) ， \(g_i=0\) 。
最后将其乘上概率 \(p\) 得方程：
然后我们发现它又可以滚动数组啊😋👍好好好。
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+50;
int n,cur;
double p,f1[2],f2[2],ans[2];
void work(){
for(int i=1;i<=n;++i){
scanf("%lf",&p);
cur^=1;
f1[cur]=0.0;
f2[cur]=0.0;
ans[cur]=0.0;
f1[cur]=(double)(f1[cur^1]+1)*p;
f2[cur]=(double)(f2[cur^1]+2*f1[cur^1]+1)*p;
ans[cur]=ans[cur^1]+(3*(f1[cur^1]+f2[cur^1])+1)*p;
}
}
int main(){
scanf("%d",&n);
work();
printf("%.1lf",ans[cur]);
}
bzoj1419 Red is good
Red is good
内存限制：256 MiB
时间限制：1000 ms
标准输入输出
题目类型：传统
评测方式：文本比较
题目描述
桌面上有R张红牌和B张黑牌，随机打乱顺序后放在桌面上，开始一张一张地翻牌，翻到红牌得到1美元，黑牌则付出1美元。可以随时停止翻牌，在最优策略下平均能得到多少钱。
输入格式
一行输入两个数R,B,其值在0到5000之间
输出格式
在最优策略下平均能得到多少钱。
样例
样例输入
5 1
样例输出
4.166666
数据范围与提示
输出答案时,小数点后第六位后的全部去掉,不要四舍五入.
解题：
这道题可太有意思了。
先说我的错误思路：
- 设 \(f_i\) 表示进行到了第 \(i\) 轮的期望， \(r_i\) 表示第 \(i\) 局摸到红球的概率， \(b_i\) 表示第\(i\) 局摸到黑球的概率，有 \(f_i=f_{i-1}+1*r_{i-1}+1*b_{i-1}\) 。
显然是错误的，因为我们的第 \(i\) 轮摸出的球的概率与第 \(i-1\) 轮摸出的球的概率不互相独立， \(r_i\) 与 \(b_i\) 是无法求出的。
2.设 \(f_{i,j}\) 表示摸到 \(i\) 个红球和 \(j\) 个黑球的期望，有 \(f_{i,j}=(f_{i-1,j}+1)*\frac{r-i+1}{r+b-i-j+1}+(f_{i,j-1}+1)*\frac{r-j+1}{r+b-i-j+1}\)
这个好像不是错误的，但是我们的答案又该从哪里找？如果是从 \(f_{R,B}\) 里找我能告诉你是错误的，而且最优策略我们也没有考虑上，考虑了摸黑牌。
而这道题，我们的期望，期望是什么，期望就是在进行这件事之前，我们预测的结果，考虑倒着推。
设\(f_{i,j}\)表示没有选择 \(i\) 个红球和 \(j\) 个黑球，有转移方程：
而我们在从 \(0\) 开始递推的时候注意判断如果为负数将这个值赋成0即可保证是最优策略。
答案是 \(f_{R,B}\)
然后我们发现还可以用滚动数组滚动一维(兄弟这可太涩了)。
但是不知道有没有可能能滚动二维，理论可行，实践失败（看我代码注释部分就知道我失败了）。
然后就是需要注意不能四舍五入！！！
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+50;
typedef long double llf;
int R,B,cur;
llf f[2][maxn],pi,pj;
int main(){
//freopen("IN.txt","r",stdin);
//freopen("QAQOUT.txt","w",stdout);
scanf("%d %d",&R,&B);
for(int i=0;i<=R;++i){
cur=cur^1;
memset(f[cur],0,sizeof(f[cur]));
for(int j=0;j<=B;++j){
//cur2=cur2^1;
if(i+j){
pi=(llf)i/(i+j);
pj=(llf)j/(i+j);
}
if(i) f[cur][j]+=(llf)(pi*(f[cur^1][j]+1));
if(j) f[cur][j]+=(llf)(pj*(f[cur][j-1]-1));
if(f[cur][j]<0) f[cur][j]=0;
//cout<<cur1<<' '<<cur2<<' ';
//cout<<f[cur][j]<<' ';
}
//cout<<endl;
}
long long s=f[cur][B]*1000000;
llf ss=(llf)s/1000000;
printf("%.6LF",ss);
//不能四舍五入
return 0;
}
TYVJ1864 守卫者的挑战
守卫者的挑战
内存限制：128 MiB
时间限制：2000 ms
标准输入输出
题目类型：传统
评测方式：文本比较
题目描述
打开了黑魔法师Vani的大门，队员们在迷宫般的路上漫无目的地搜寻着关押applepi的监狱的所在地。突然，眼前一道亮光闪过。“我，Nizem，是黑魔法圣殿的守卫者。如果你能通过我的挑战，那么你可以带走黑魔法圣殿的地图……”瞬间，队员们被传送到了一个擂台上，最初身边有一个容量为K的包包。
擂台赛一共有N项挑战，各项挑战依次进行。第i项挑战有一个属性ai，如果ai>=0，表示这次挑战成功后可以再获得一个容量为ai的包包；如果ai=-1，则表示这次挑战成功后可以得到一个大小为1 的地图残片。地图残片必须装在包包里才能带出擂台，包包没有必要全部装满，但是队员们必须把 【获得的所有的】地图残片都带走（没有得到的不用考虑，只需要完成所有N项挑战后背包容量足够容纳地图残片即可），才能拼出完整的地图。并且他们至少要挑战成功L次才能离开擂台。
队员们一筹莫展之时，善良的守卫者Nizem帮忙预估出了每项挑战成功的概率，其中第i项挑战成功的概率为pi%。现在，请你帮忙预测一下，队员们能够带上他们获得的地图残片离开擂台的概率。
输入格式
第一行三个整数N,L,K。
第二行N个实数，第i个实数pi表示第i项挑战成功的百分比。
第三行N个整数，第i个整数ai表示第i项挑战的属性值.
输出格式
一个整数，表示所求概率，四舍五入保留6 位小数。
样例
样例输入1
3 1 0
10 20 30
-1 -1 2
样例输出1
0.300000
样例输入2
5 1 2
36 44 13 83 63
-1 2 -1 2 1
样例输出2
0.980387
数据范围与提示
若第三项挑战成功，如果前两场中某场胜利，队员们就有空间来容纳得到的地图残片，如果挑战失败，根本就没有获得地图残片，不用考虑是否能装下；
若第三项挑战失败，如果前两场有胜利，没有包来装地图残片，如果前两场都失败，不满足至少挑战成功次（）的要求。因此所求概率就是第三场挑战获胜的概率。
对于 100% 的数据，保证0<=K<=2000，0<=N<=200，-1<=ai<=1000，0<=L<=N，0<=pi<=100
解题：
这道题我一开始想的是预处理出所有的背包容积概率（
但是码代码的时候我突然明白一件事：如果两个背包容积是一样的，该怎么办？那这个思路就肯定会寄。
正解应是酱紫：
设 \(f_{i,j,k}\) 表示进行了 \(i\) 次比赛， \(j\) 次胜利， \(k\) 为背包容积，的概率。
然后因为 \(k\) 很大，但是我们的 \(n\) 很小，超出 \(n\) 大小的背包是没有意义的，所以可以将较大的第三维转换为较小的 \(n*2\) ，使小于 \(n\) 的表示不能带走所有获得的地图碎片。
于是有转移：
然后我们发现这个又可以用滚动数组滚一维（？）
如果这道题不用滚动数组的话开 \(long\) \(double\) 会 \(MLE\) 。（当然也不是必须开 \(long\) \(double\)，主要是因为博主胆小好色看到六位小数就想开）
tmd感觉快成滚动数组学习笔记了怎么会这样
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=250,maxk=2e3+50;
typedef long double llf;
int n,l,k,a[maxn],cur;
llf p[maxn],f[2][maxn][maxn<<1];
void input(){
int in;
scanf("%d %d %d",&n,&l,&k);
k=min(n,k);
for(int i=1;i<=n;++i){
scanf("%d",&in);
p[i]=(llf)in/100;
}
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
a[i]=min(a[i],n);
}
f[0][0][200+k]=1.0;
}
void work(){
for(int i=1;i<=n;++i){
cur=cur^1;
memset(f[cur],0,sizeof(f[cur]));
for(int j=0;j<=i;++j){
for(int k=0;k<=400;++k){
f[cur][j][k]=(llf)f[cur][j][k]+f[cur^1][j][k]*(llf)(1-p[i]);
if(j>=1 && k-a[i]>=0) f[cur][j][k]=(llf)f[cur][j][k]+f[cur^1][j-1][k-a[i]]*p[i];
//cout<<f[cur][j][k]<<endl;
}
}
}
}
int main(){
//freopen("In.txt","r",stdin);
//freopen("QAQOUT.TXT","w",stdout);
input();
work();
llf ans=0.0;
for(int i=l;i<=n;++i){
for(int j=200;j<=400;++j){
ans=(llf)ans+f[cur][i][j];
}
}
printf("%.6Lf",ans);
return 0;
}
BZOJ 2720列队春游
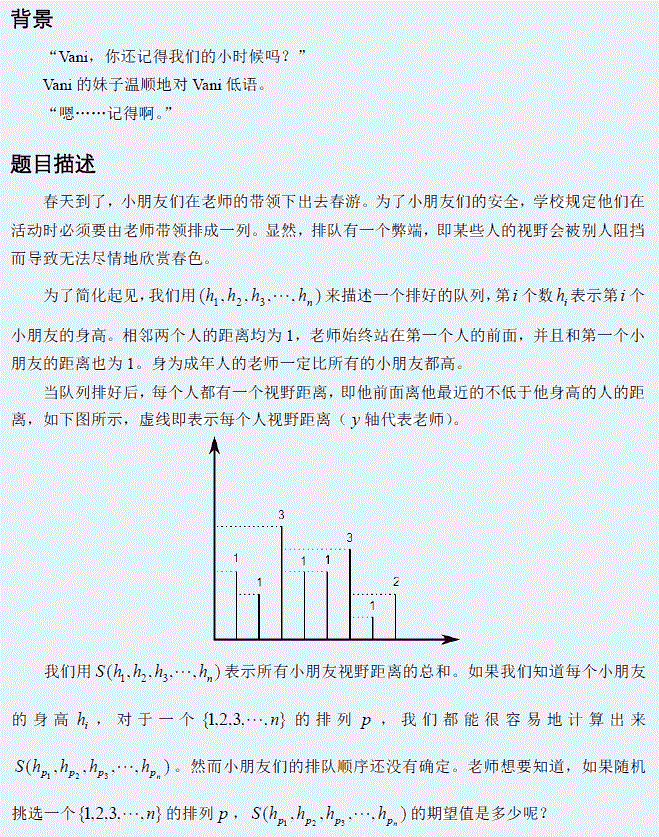
样例：
输入样例：
3
1 2 3
输出样例：
4.33
解题：
两种做法：
- \(O(n)\) 做法
这道题不是要求总期望嘛，根据期望的线性性质，那我们肯定要求个人期望的对吧。
我们先考虑如何计算个人期望，根据全期望公式，我们可以将期望分解：
每种视野的视野长度*该种视野概率。
即
其中， \(i\) 是我们枚举的视野距离， \(p(len)\) 则是这种视野距离的概率。
然后这个式子是可以被转换的。
可见下表格：
| \(p_1\) | \(p_2\) | \(p_3\) | \(p_{…}\) | \(p_n\) |
|---|---|---|---|---|
| \(p_2\) | \(p_3\) | \(p_{…}\) | \(p_n\) | |
| \(p_3\) | \(p_{…}\) | \(p_n\) | ||
| \(p_{…}\) | \(p_n\) | |||
| \(p_n\) | ||||
| …… |
这是我们原本的式子 \(\sum_{i=1}^{n} i \times p(len)\) 计算的东西，第一列是 \(i==1\) ，第二列是 \(i==2\) ，以此类推，而且每增加一列就增加一行，因此行数==列数，原本的式子我们是列列相加，现在我们改成行行相加，从上向下加，得到一个更加简洁的式子：
对于这个式子也可以感性理解：如果说上一个式子是枚举距离乘上概率，这个式子就是枚举这个人前面的第 \(i\) 位的人有多大的概率被看到，其贡献为 \(1\) 。
现在我们考虑如何求出 \(p(len>=i)\)
设身高比这个人高的人数为 \(k\) （不包括其自身），那么能挡住这个人的所有人和他自己排列有 \(A_n^{k+1}\) 种方案，而其视野长度为 \(i\) ，而对于合法的方案来说，在视野内不可能有比ta高的人，所以那些能挡住ta的人的位置应有 \(A_{n-i}^k\) 种方案，这个人之前还必须有 \(i-1\) 个人，ta的位置有 \(n-i+1\) 种方案。
于是：\(p(len>=i)=\frac{(n-i+1)A_{n-i}^{k}}{A_{n}^{k+1}}\)
然后把排列数拆开，开始我们恶心的推导……
解释一下（？），感觉也不用解释：
1——》2：可以提出一个常数 \(\frac {(n-k-1)!}{n!}\)
2——》4：\((n-i+1)-(n-i-k)=(k+1)\) ,提出一个常数 \((k+1)\)! 可以化为组合数 \(\textrm{C} _{n-i+1}^{k+1}\)
4——》5：根据\(\sum\limits_{i=0}^n \textrm{C}_{k}^{i}=\textrm{C}_{k+1}^{n+1}\)易得.
Miku's Code
#include<bits/stdc++.h>
using namespace std;
typedef long double llf;
const int maxn=3e2+50,maxh=1e3+50;
int n,height,h[maxh],k;
llf ans;
void input(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&height);
++h[height];
}
}
void work(){
for(int i=1;i<=1000;++i){
ans=(llf)ans+(llf)h[i]*(n+1)/(n-k+1);
//k是比ta低的人
k=k+h[i];
}
}
int main(){
input();
work();
printf("%.2Lf",ans);
}
- \(O(n^2)\) 做法
第二种做法是 \(O(n^2)\) 的。
这里我必须推一下小天使的博客：超绝最可爱天使酱的列队春游题解
其实 \(O(n^2)\) 比 \(O(n)\) 好想的不是一点半点，以至于我个人认为 \(O(n^2)\) 才是正解（
谁都能想到 \(O(n^3)\) 暴力，无脑枚举身高+位置+视野长度期望，一眼会T，就看你敢不敢尝试（笑）
排列嘛，排列的前缀后缀是可以重复的啊，只要调换一个顺序，这意味着不同位置的相同长度，会造成重复的计算，所以考虑优化。
所以还枚举什么位置，而是去枚举视野长度。
设 \(s\) 是比某人矮的人数，那么对于长度 \(len\) ，其概率为
相当于一个个往前放矮子嘛，高个后放随便乱排。
Miku's Code
#include<bits/stdc++.h>
using namespace std;
typedef double llf;
const int maxn=3e2+50,maxh=1e3+50;
int n,h[maxn],qp[maxh],k;
llf ans;
void input(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&h[i]);
}
sort(h+1,h+1+n);
for(int i=1;i<=n;++i){
if(!qp[h[i]]) qp[h[i]]=i;
}
}
void work(){
for(int i=1;i<=n;++i){
llf p=1.0;
for(int j=1;j<=n;++j){
ans=ans+p*(n-j+1)/n;
if(j==n) break;
p=p/(n-j)*(qp[h[i]]-j);
}
}
}
int main(){
input();
work();
printf("%.2lf",ans);
return 0;
}
bzoj2969 矩形粉刷
矩形粉刷
内存限制：256 MiB
时间限制：1000 ms
标准输入输出
题目类型：传统
评测方式：文本比较
题目描述
为了庆祝新的一年到来，小M决定要粉刷一个大木板。大木板实际上是一个 \(W*H\) 的方阵。小M得到了一个神奇的工具，这个工具只需要指定方阵中两个格子，就可以把这两格子为对角的，平行于木板边界的一个子矩形全部刷好。小M乐坏了，于是开始胡乱地使用这个工具。
假设小M每次选的两个格子都是完全随机的（方阵中每个格子被选中的概率是相等的），而且小M使用了 \(K\) 次工具，求木板上被小M粉刷过的格子个数的期望值是多少。
输入格式
第一行是整数K，W，H
输出格式
一行，为答案，四舍五入保留到整数。
样例
样例输入
1 3 3
样例输出
4
样例解释
准确答案约为3.57
数据范围与提示
100% 的数据满足：\(1 ≤ W, H ≤ 1000， 0 ≤ K ≤ 100\)
解题：
刷色嘛，设被涂色的期望是 \(1\)，根据全期望公式，粉刷过格子个数的期望，就是每个点被涂色的概率的和。
然而，如果考虑涂色 \(k\) 次，我们先假设 \(k==2\) 来举个例子，显然某个格子被涂色的概率是：
\(p_2=p_1+p_1-p_1*p_1\)
\(p_i\) 表示第 \(1\) 轮到第 \(i\) 轮被涂色过的概率。
那这就要考虑多步容斥了，但是众所周知我是个废物，所以不会（好吧如果真的想看可以去翻找一下我的二项式定理和反演证明）
我的高中数学老师告诉我多步容斥很多时候都可以用“正难则反”解决（
我们现在假设 \(p_i\) 表示第 \(1\) 轮到第 \(i\) 轮某个格子没有被涂色的概率：
\(p_i=\prod\limits_{i=1}^np_1\)
求被涂色期望就直接 \(1-p_i\) 。
所以我们需要的就只是 \(p_1\) 。
最初考虑的是枚举选两次的全部点数，然后相加每次选的概率，显然时间复杂度是 \(O(K^2*W^2)\) 的。
感觉很简单的问题，但是这个时间复杂度我不太能恭维……
然后其实可以枚举所有点数，直接两部容斥算出它不被涂色的概率，对于一个矩阵中的一个点来说：
- 如果这个点上边的两个点或下边的两个点被选择了，那么这个点不会被涂色：
p1=Pow(1.0*(i-1)/w,2)+Pow(1.0*(w-i)/w,2)
- 如果这个点左边的两个点或右边的两个点被选择了，那么这个点不会被涂色：
p2=Pow(1.0*(j-1)/h,2)+Pow(1.0*(h-j)/h,2)
- 如果都在这个点左上角的两个点被选择了，那么这个点不会被涂色：
p3=Pow(1.0*(i-1)/w,2)*Pow(1.0*(j-1)/h,2)
- 如果都在这个点左下角的两个点被选择了，那么这个点不会被涂色：
p4=Pow(1.0*(i-1)/w,2)*Pow(1.0*(h-j)/h,2)
- 如果都在这个点右上角的两个点被选择了，那么这个点不会被涂色：
p5=Pow(1.0*(w-i)/w,2)*Pow(1.0*(j-1)/h,2)
- 如果都在这个点右下角的两个点被选择了，那么这个点不会被涂色：
p6=Pow(1.0*(w-i)/w,2)*Pow(1.0*(h-j)/h,2)
然后自己画个矩阵容斥吧，
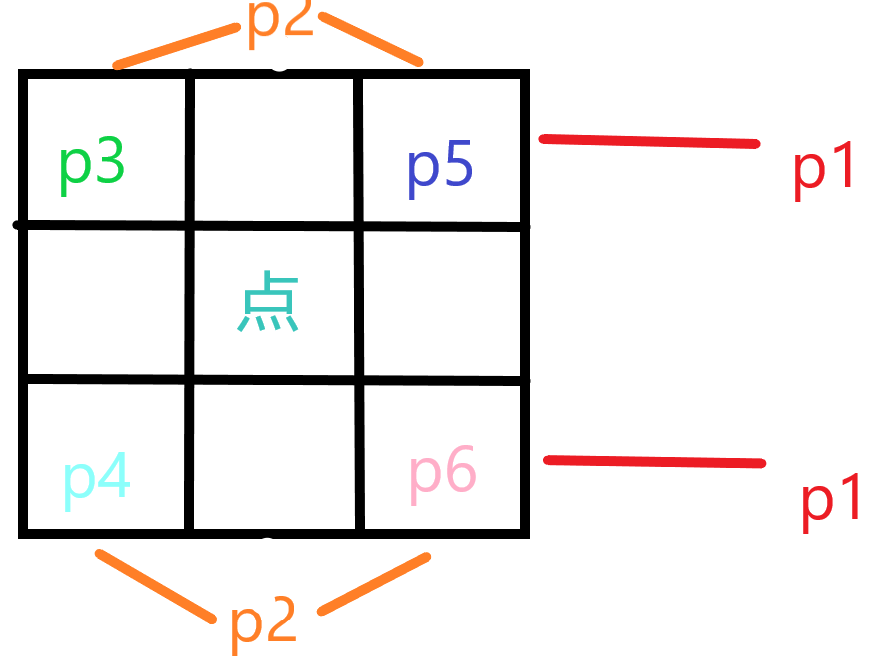
显然 \(p=p1+p2-p3-p4-p5-p6\) 。
闲话：为什么是平方？
（图片出自【LGR-147】作弊惩罚公示，kkk回复“代码相似纯属巧合”）
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+50,maxk=105;
int k,w,h;
double p[maxn][maxn];
double Pow(double a,int x){
double s=1.0;
while(x--) s*=a;
return s;
}
#define p1 (double)Pow(1.0*(i-1)/w,2)+Pow(1.0*(w-i)/w,2)
#define p2 (double)Pow(1.0*(j-1)/h,2)+Pow(1.0*(h-j)/h,2)
#define p3 (double)Pow(1.0*(i-1)/w,2)*Pow(1.0*(j-1)/h,2)
#define p4 (double)Pow(1.0*(i-1)/w,2)*Pow(1.0*(h-j)/h,2)
#define p5 (double)Pow(1.0*(w-i)/w,2)*Pow(1.0*(j-1)/h,2)
#define p6 (double)Pow(1.0*(w-i)/w,2)*Pow(1.0*(h-j)/h,2)
void get(){
for(int i=1;i<=w;++i){
for(int j=1;j<=h;++j){
p[i][j]=p1+p2-p3-p4-p5-p6;
}
}
}
int main(){
scanf("%d %d %d",&k,&w,&h);
get();
double ans=0;
for(int i=1;i<=w;++i){
for(int j=1;j<=h;++j){
ans=(double)ans+(1-pow(p[i][j],k));
}
}
//printf("%lf\n",ans);
int ansl=floor(ans+0.5);
//floor向下取整
printf("%d",ansl);
return 0;
}
[JLOI2013] 卡牌游戏
[JLOI2013] 卡牌游戏
题目描述
N个人坐成一圈玩游戏。一开始我们把所有玩家按顺时针从1到N编号。首先第一回合是玩家1作为庄家。每个回合庄家都会随机（即按相等的概率）从卡牌堆里选择一张卡片，假设卡片上的数字为X，则庄家首先把卡片上的数字向所有玩家展示，然后按顺时针从庄家位置数第X个人将被处决即退出游戏。然后卡片将会被放回卡牌堆里并重新洗牌。被处决的人按顺时针的下一个人将会作为下一轮的庄家。那么经过N-1轮后最后只会剩下一个人，即为本次游戏的胜者。现在你预先知道了总共有M张卡片，也知道每张卡片上的数字。现在你需要确定每个玩家胜出的概率。
这里有一个简单的例子：
例如一共有4个玩家，有四张卡片分别写着3,4,5,6.
第一回合，庄家是玩家1，假设他选择了一张写着数字5的卡片。那么按顺时针数1,2,3,4,1，最后玩家1被踢出游戏。
第二回合，庄家就是玩家1的下一个人，即玩家2.假设玩家2这次选择了一张数字6，那么2,3,4,2,3,4，玩家4被踢出游戏。
第三回合，玩家2再一次成为庄家。如果这一次玩家2再次选了6，则玩家3被踢出游戏，最后的胜者就是玩家2.
输入格式
第一行包括两个整数N,M分别表示玩家个数和卡牌总数。
接下来一行是包含M个整数，分别给出每张卡片上写的数字。
输出格式
输出一行包含N个百分比形式给出的实数，四舍五入到两位小数。分别给出从玩家1到玩家N的胜出概率，每个概率之间用空格隔开，最后不要有空格。
样例 #1
样例输入 #1
5 5
2 3 5 7 11
样例输出 #1
22.72% 17.12% 15.36% 25.44% 19.36%
样例 #2
样例输入 #2
4 4
3 4 5 6
样例输出 #2
25.00% 25.00% 25.00% 25.00%
提示
对于30%的数据，有1<=N<=10
对于50%的数据，有1<=N<=30
对于100%的数据，有1<=N<=50 1<=M<=50 1<=每张卡片上的数字<=50
解题：
如果有人感兴趣的话可以优化一下我的代码（），没写快读。
（但是这个最优解就跟测运气一样，看服务器波动多大，绷不住了）
这个题和 \(Red\) \(is\) \(good\) 很像，就是我们的上一次抽卡和下一次抽卡它们之间并不相互独立。
所以我们采取和 \(Red\) \(is\) \(good\) 相似的解法：倒推。
设 \(f_{i,j}\) 表示环内还剩 \(i\) 人时，第 \(j\) 个人获胜的概率。
那么有边界： \(f_{1,1}=1.0\)
转移方程：
\(k\) 是枚举的上一局获胜的人。
然后我们发现它它它叕可以滚动数组(＾－＾)V
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=51;
int n,m,card[maxn],cur;
double f[2][maxn];
//f[i][j]表示环内还剩i人时,第j人获胜的概率
void input(){
scanf("%d %d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d",&card[i]);
}
f[cur][1]=1.0;
//只有一个人在环内胜率伯分之伯
}
void clear(){
for(int j=1;j<=n;++j){
f[cur][j]=0;
}
}
void work(){
int gout;
for(int i=2;i<=n;++i){
cur=cur^1;
clear();
for(int j=1;j<=m;++j){
if(card[j]%i==0) gout=i;
else gout=card[j]%i;
for(int k=1;k<=i-1;++k){
++gout;
if(gout>i) gout=1; //环
f[cur][gout]=f[cur][gout]+f[cur^1][k]/(double)m;
}
}
}
}
int main(){
input();
work();
for(int i=1;i<=n-1;++i){
f[cur][i]=f[cur][i]*100;
printf("%.2lf",f[cur][i]);
putchar('%');
putchar(' ');
}
f[cur][n]=f[cur][n]*100;
printf("%.2lf%",f[cur][n]);
putchar('%');
return 0;
}
[NOIP2016 提高组] 换教室
[NOIP2016 提高组] 换教室
题目描述
对于刚上大学的牛牛来说，他面临的第一个问题是如何根据实际情况申请合适的课程。
在可以选择的课程中，有 \(2n\) 节课程安排在 \(n\) 个时间段上。在第 \(i\)（\(1 \leq i \leq n\)）个时间段上，两节内容相同的课程同时在不同的地点进行，其中，牛牛预先被安排在教室 \(c_i\) 上课，而另一节课程在教室 \(d_i\) 进行。
在不提交任何申请的情况下，学生们需要按时间段的顺序依次完成所有的 \(n\) 节安排好的课程。如果学生想更换第 \(i\) 节课程的教室，则需要提出申请。若申请通过，学生就可以在第 \(i\) 个时间段去教室 \(d_i\) 上课，否则仍然在教室 \(c_i\) 上课。
由于更换教室的需求太多，申请不一定能获得通过。通过计算，牛牛发现申请更换第 \(i\) 节课程的教室时，申请被通过的概率是一个已知的实数 \(k_i\)，并且对于不同课程的申请，被通过的概率是互相独立的。
学校规定，所有的申请只能在学期开始前一次性提交，并且每个人只能选择至多 \(m\) 节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请；牛牛可以申请自己最希望更换教室的 \(m\) 门课程，也可以不用完这 \(m\) 个申请的机会，甚至可以一门课程都不申请。
因为不同的课程可能会被安排在不同的教室进行，所以牛牛需要利用课间时间从一间教室赶到另一间教室。
牛牛所在的大学有 \(v\) 个教室，有 \(e\) 条道路。每条道路连接两间教室，并且是可以双向通行的。由于道路的长度和拥堵程度不同，通过不同的道路耗费的体力可能会有所不同。 当第 \(i\)（\(1 \leq i \leq n-1\)）节课结束后，牛牛就会从这节课的教室出发，选择一条耗费体力最少的路径前往下一节课的教室。
现在牛牛想知道，申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小，请你帮他求出这个最小值。
输入格式
第一行四个整数 \(n,m,v,e\)。\(n\) 表示这个学期内的时间段的数量；\(m\) 表示牛牛最多可以申请更换多少节课程的教室；\(v\) 表示牛牛学校里教室的数量；\(e\)表示牛牛的学校里道路的数量。
第二行 \(n\) 个正整数，第 \(i\)（\(1 \leq i \leq n\)）个正整数表示 \(c_i\)，即第 \(i\) 个时间段牛牛被安排上课的教室；保证 \(1 \le c_i \le v\)。
第三行 \(n\) 个正整数，第 \(i\)（\(1 \leq i \leq n\)）个正整数表示 \(d_i\)，即第 \(i\) 个时间段另一间上同样课程的教室；保证 \(1 \le d_i \le v\)。
第四行 \(n\) 个实数，第 \(i\)（\(1 \leq i \leq n\)）个实数表示 \(k_i\)，即牛牛申请在第 \(i\) 个时间段更换教室获得通过的概率。保证 \(0 \le k_i \le 1\)。
接下来 \(e\) 行，每行三个正整数 \(a_j, b_j, w_j\)，表示有一条双向道路连接教室 \(a_j, b_j\)，通过这条道路需要耗费的体力值是 \(w_j\)；保证 \(1 \le a_j, b_j \le v\)， \(1 \le w_j \le 100\)。
保证 \(1 \leq n \leq 2000\)，\(0 \leq m \leq 2000\)，\(1 \leq v \leq 300\)，\(0 \leq e \leq 90000\)。
保证通过学校里的道路，从任何一间教室出发，都能到达其他所有的教室。
保证输入的实数最多包含 \(3\) 位小数。
输出格式
输出一行，包含一个实数，四舍五入精确到小数点后恰好\(2\)位，表示答案。你的输出必须和标准输出完全一样才算正确。
测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 \(4 \times 10^{-3}\)。 （如果你不知道什么是浮点误差，这段话可以理解为：对于大多数的算法，你可以正常地使用浮点数类型而不用对它进行特殊的处理）
样例 #1
样例输入 #1
3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5
1 2 5
1 3 3
2 3 1
样例输出 #1
2.80
提示
【样例1说明】
所有可行的申请方案和期望收益如下表:
【提示】
- 道路中可能会有多条双向道路连接相同的两间教室。 也有可能有道路两端连接的是同一间教室。
- 请注意区分n,m,v,e的意义, n不是教室的数量, m不是道路的数量。
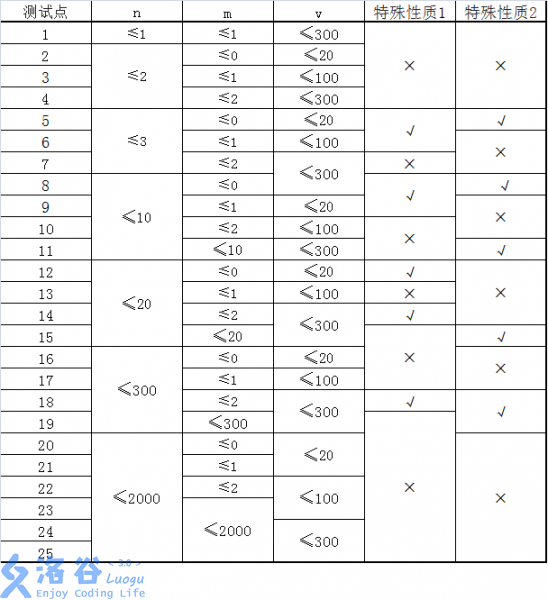
特殊性质1:图上任意两点 \(a_i\), \(b_i\), \(a_i\)≠ \(b_i\)间,存在一条耗费体力最少的路径只包含一条道路。
特殊性质2:对于所有的 \(1≤ i≤ n\)， \(k_i= 1\) 。
解题：
这道题也好有意思（起码题干描述是这样的）
这个题最重要的一点就是告诉你，换教室的机会是申请计数，你必须考虑换教室是一个概率成功事件，但是无论成功还是失败都一定会消耗你的申请次数。
最初想的就是设 \(f_{i,j}\) 表示时间段 \(i\) 上一次教室为 \(j\) 的体力期望然后转移。
但是这么想忽略了一个很重要的条件：只能 申请 换 \(m\) 次教室，在输入说明中提到。
而且还可以优化，因为上一次教室无非两种可能： \(c_{i-1}\) 或者 \(d_{i-1}\) 。
所以原本的第二维可以优化成换不换的\(01\)问题，中间再加一维统计 申请 换教室的次数就好了。
设 \(f_{i,j,k}\) 表示第 \(i\) 时间段，已经 申请 换过 \(j\) 次教室（计算本次是否 申请 更换），第 \(i\) 时间段 申请 换不换教室的期望，\(k==0\) 表示不 申请 换教室，\(k==1\) 表示申请 换教室。
有：
我去，介么长
别急还有更长的
解释一下：
\(f_{i-1,j,0}\) 表示上次就没 申请 换教室的期望，所以第 \(i-1\) 时间段一定是在 \(c_{i-1}\) 该教室上课，概率为 \(100%\)。
\(f_{i-1,j,1}\) 表示上次 申请了 换教室（不意味着一定成功），所以第 \(i-1\) 时间段有 \(p_{i-1}\) 的可能在 \(d_{i-1}\) 该教室上课，有 \(1-p_{i-1}\) 的可能在 \(c_{i-1}\) 的教室上课，于是根据全期望公式得上式。
其实倒不是多么难，就是看起来挺哈人
来解释一下：
\(f_{i-1,j-1,0}\) 表示上次就没 申请 换教室的期望，所以 \(i-1\) 时间段一定在 \(c_{i-1}\) 教室上课，但是因为我们第 \(i\) 时间段选择了 申请 换教室，所以在第 \(i\) 时间段有 \(p_i\) 的可能在 \(d_i\) 上课，\(1-p_i\) 的可能在 \(c_i\) 上课。
相似的：
\(f_{i-1,j-1,1}\) 是上次 申请了 换教室的期望，所以 \(i-1\) 时间段有 \(p_{i-1}\) 的可能在 \(d_{i-1}\) 上课，有 \(1-p_{i-1}\) 的可能在 \(c_{i-1}\) 上课，而在第 \(i\) 时间段，有 \(p_i\) 的可能在 \(d_i\) 上课，\(1-p_i\) 的可能在 \(c_i\) 上课。
所以边界就是 \(f_{1,0,0}=f_{1,1,1}=0\)。
然后我们就考虑如何算出路径，这不是要求只连一个点，而且 \(v<=300\) 很小，果断放弃 \(dijkstra\)，选择我们的 \(Flyoed\)。
记得初始值赋最大。
注意有点有自环。
\(O(v^3)\) 的预处理完全可以接受，而动态转移则是 \(O(n\times m\times 2)\)。
然后这个题还能滚动数组欸(●ˇ∀ˇ)
这个滚动数组太好了，因为他不止可以帮你优化动态空间，还可以优化你的初始化时间。
（最后虽然不是最优解，但是挤进优解第一页了，虽然是倒数第二个一个。。。）
（感兴趣的可以继续优化）
（这个码风我救不了，最长303列，我也没办法，它这个转移就这么长……）
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=2050,maxm=2050,maxv=305,maxe=90050;
#define MYMAX 191981000
inline int read(){
char c=getchar();
int x=0,f=1;
while(c<48){if(c=='-')f=-1;c=getchar();}
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
int n,m,v,e,cur;
int c[maxn],d[maxn];
double p[maxn],f[2][maxm][2];
int dis[maxm][maxm];
void input(){
n=read(),m=read(),v=read(),e=read();
for(int i=1;i<=v;++i){
for(int j=1;j<i;++j){
dis[j][i]=dis[i][j]=MYMAX;
}
}
//有自环注意dis[i][i]=0
for(int j=0;j<=m;++j){
f[cur][j][1]=f[cur][j][0]=f[cur^1][j][1]=f[cur^1][j][0]=MYMAX;
}
f[cur][0][0]=f[cur][1][1]=0;
for(int i=1;i<=n;++i){
c[i]=read();
}
for(int i=1;i<=n;++i){
d[i]=read();
}
for(int i=1;i<=n;++i){
scanf("%lf",&p[i]);
}
int u,v,w;
for(int i=1;i<=e;++i){
u=read(),v=read(),w=read();
w=min(dis[u][v],w);
//有自环注意
dis[u][v]=w;
dis[v][u]=w;
}
}
void Floyed(){
for(int k=1;k<=v;++k){
for(int i=1;i<=v;++i){
for(int j=1;j<=v;++j){
if(dis[i][k]+dis[k][j]<dis[i][j]){
dis[j][i]=dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
}
}
void clear(){
for(int j=0;j<=m;++j){
f[cur][j][0]=f[cur][j][1]=MYMAX;
}
}
void work(){
for(int i=2;i<=n;++i){
cur=cur^1;
//clear();没必要因为我们没有用到当前状态
int len=min(m,i);
for(int j=0;j<=len;++j){
f[cur][j][0]=min(f[cur^1][j][0]+(double)dis[c[i-1]][c[i]],f[cur^1][j][1]+(double)dis[d[i-1]][c[i]]*p[i-1]+(double)dis[c[i-1]][c[i]]*(1-p[i-1]));
if(j>0)
f[cur][j][1]=min(f[cur^1][j-1][0]+(double)dis[c[i-1]][d[i]]*p[i]+(double)dis[c[i-1]][c[i]]*(1-p[i]),f[cur^1][j-1][1]+(double)dis[d[i-1]][d[i]]*p[i-1]*p[i]+(double)dis[c[i-1]][d[i]]*(1-p[i-1])*p[i]+(double)dis[d[i-1]][c[i]]*p[i-1]*(1-p[i])+(double)dis[c[i-1]][c[i]]*(1-p[i-1])*(1-p[i]));
//printf("###%d %.2lf %.2lf\n",j,f[cur][j][0],f[cur][j][1]);
}
}
}
int main(){
//freopen("P1850_2.in","r",stdin);
//freopen("MOUT.txt","w",stdout);
input();
Floyed();
work();
double ans=MYMAX;
for(int j=0;j<=m;++j){
ans=min(f[cur][j][0],min(ans,f[cur][j][1]));
}
printf("%.2lf",ans);
return 0;
}
[SCOI2008] 奖励关
[SCOI2008] 奖励关
题目描述
你正在玩你最喜欢的电子游戏，并且刚刚进入一个奖励关。在这个奖励关里，系统将依次随机抛出 \(k\) 次宝物，每次你都可以选择吃或者不吃（必须在抛出下一个宝物之前做出选择，且现在决定不吃的宝物以后也不能再吃）。
宝物一共有 \(n\) 种，系统每次抛出这 \(n\) 种宝物的概率都相同且相互独立。也就是说，即使前 \((k-1)\) 次系统都抛出宝物 \(1\)（这种情况是有可能出现的，尽管概率非常小），第 \(k\) 次抛出各个宝物的概率依然均为 $\frac 1 n $。
获取第 \(i\) 种宝物将得到 \(p_i\) 分，但并不是每种宝物都是可以随意获取的。第 \(i\) 种宝物有一个前提宝物集合 \(s_i\)。只有当 \(s_i\) 中所有宝物都至少吃过一次，才能吃第 \(i\) 种宝物（如果系统抛出了一个目前不能吃的宝物，相当于白白的损失了一次机会）。注意，\(p_i\) 可以是负数，但如果它是很多高分宝物的前提，损失短期利益而吃掉这个负分宝物将获得更大的长期利益。
假设你采取最优策略，平均情况你一共能在奖励关得到多少分值？
输入格式
第一行为两个整数，分别表示抛出宝物的次数 \(k\) 和宝物的种类数 \(n\)。
第 \(2\) 到第 \((n + 1)\) 行，第 \((i + 1)\) 有若干个整数表示第 \(i\) 个宝物的信息。每行首先有一个整数，表示第 \(i\) 个宝物的分数 \(p_i\)。接下来若干个互不相同的整数，表示该宝物的各个前提宝物集合 \(s_i\)，每行的结尾是一个整数 \(0\)，表示该行结束。
输出格式
输出一行一个实数表示答案，保留六位小数。
样例1：
样例输入 #1
1 2
1 0
2 0
样例输出 #1
1.500000
样例 #2
样例输入 #2
6 6
12 2 3 4 5 0
15 5 0
-2 2 4 5 0
-11 2 5 0
5 0
1 2 4 5 0
样例输出 #2
10.023470
提示
数据规模与约定
对于全部的测试点，保证 \(1 \leq k \leq 100\)，\(1 \leq n \leq 15\)，\(-10^6 \leq p_i \leq 10^6\)。
解题：
为什么倒推见 全期望公式 部分。
这道题还是符合我们的规律，就是上一个选择的物品对下次选择有影响，从这方面选择倒推也是正确的。
然后可以使用滚动数组，就酱紫吧，今天抠了一天为什么倒推，如果不对那对不起，可以在评论区指出。
转移状态自己看洛谷题解，累了呜。
Miku's Code
#include<bits/stdc++.h>
using namespace std;
typedef long double llf;
#define fs (1<<n)-1
const int maxn=17,maxk=105;
int n,k,p[maxn],LS,limits[(1<<15)],cur;
llf f[2][(1<<15)];
//f[i][s]表示在第i轮状态为s时的最大期望得分
llf Max(llf f1,llf f2){
if(f1<f2) return f2;
else return f1;
}
void input(){
scanf("%d %d",&k,&n);
for(int i=1;i<=n;++i){
scanf("%d",&p[i]);
while(scanf("%d",&LS) && LS!=0){
limits[i]=limits[i]|(1<<(LS-1));
}
}
}
void clear(){
for(int s=0;s<=fs;++s){
f[cur][s]=0;
}
}
void work(){
for(int i=k;i>=1;--i){ //逆推
cur=cur^1;
clear();
for(int s=0;s<=fs;++s){ //枚举状态
for(int j=1;j<=n;++j){
if((limits[j]&s)==limits[j]){
f[cur][s]=f[cur][s]+Max(f[cur^1][s],(llf)f[cur^1][s|(1<<(j-1))]+p[j]);
//cout<<f[i][s]<<' '<<f[i+1][s|limits[j]]+p[j]<<endl;
}
else{
f[cur][s]=f[cur][s]+f[cur^1][s];
}
}
f[cur][s]=(llf)f[cur][s]/n;
}
}
}
int main(){
input();
work();
printf("%.6Lf",f[cur][0]);
return 0;
}
[SHOI2014] 概率充电器
[SHOI2014] 概率充电器
题目描述
著名的电子产品品牌 SHOI 刚刚发布了引领世界潮流的下一代电子产品——概率充电器：
“采用全新纳米级加工技术，实现元件与导线能否通电完全由真随机数决定！SHOI 概率充电器，您生活不可或缺的必需品！能充上电吗？现在就试试看吧！”
SHOI 概率充电器由 \(n-1\) 条导线连通了 \(n\) 个充电元件。进行充电时，每条导线是否可以导电以概率决定，每一个充电元件自身是否直接进行充电也由概率决定。随后电能可以从直接充电的元件经过通电的导线使得其他充电元件进行间接充电。
作为 SHOI 公司的忠实客户，你无法抑制自己购买 SHOI 产品的冲动。在排了一个星期的长队之后终于入手了最新型号的 SHOI 概率充电器。你迫不及待地将 SHOI 概率充电器插入电源——这时你突然想知道，进入充电状态的元件个数的期望是多少呢？
输入格式
第一行一个整数 \(n\)。概率充电器的充电元件个数。充电元件由 \(1 \sim n\) 编号。
之后的 \(n-1\) 行每行三个整数 \(a, b, p\)，描述了一根导线连接了编号为 \(a\) 和 \(b\) 的充电元件，通电概率为 \(p\%\)。
第 \(n+2\) 行 \(n\) 个整数 \(q_i\)。表示 \(i\) 号元件直接充电的概率为 \(q_i\%\)。
输出格式
输出一行一个实数，为能进入充电状态的元件个数的期望，四舍五入到小数点后 6 位小数。
样例 #1
样例输入 #1
3
1 2 50
1 3 50
50 0 0
样例输出 #1
1.000000
样例 #2
样例输入 #2
5
1 2 90
1 3 80
1 4 70
1 5 60
100 10 20 30 40
样例输出 #2
4.300000
提示
对于 \(30\%\) 的数据，\(n \leq 5 \times 10^3\)。
对于 \(100\%\) 的数据，\(n \leq 5 \times 10^5\)，\(0 \leq p,q_i \leq 100\)。
解题：
逆天题目。
看题解才看会。
树形 \(dp\) 复习。
首先我们要明确所有点贡献为 \(1\)，所以我们求的能进入充电状态的元件的期望就是概率和 \(\sum_{i=1}^{n} \limits p_i\)。
而节点 \(i\) 的来电可能有三种情况：
-
自己来电。
-
儿子来电且通过导线传给自己。
-
父亲来电且通过导线传给自己。
于是我们可以拆分两个问题，分成 \(up\) 问题和 \(down\) 问题，首先先考虑第二种情况，\(up\) 问题：
设 \(p_i\) 表示来电的概率，\(w_{i,j}\)表示节点 \(i\) 与节点 \(j\) 之间导线可以导电的概率，初始值是其本身的来电概率。
第一遍 \(up\)_\(dfs\) 中，来电有两种情况：
-
根自己来电。
-
儿子来电导线传达。
根据容斥原理得：
现在我们的 \(p_i\) 的定义就不再是本身来电概率了，而是子树来电概率（包括其自身），那么如何考虑\(down\)_\(dfs\) 呢？
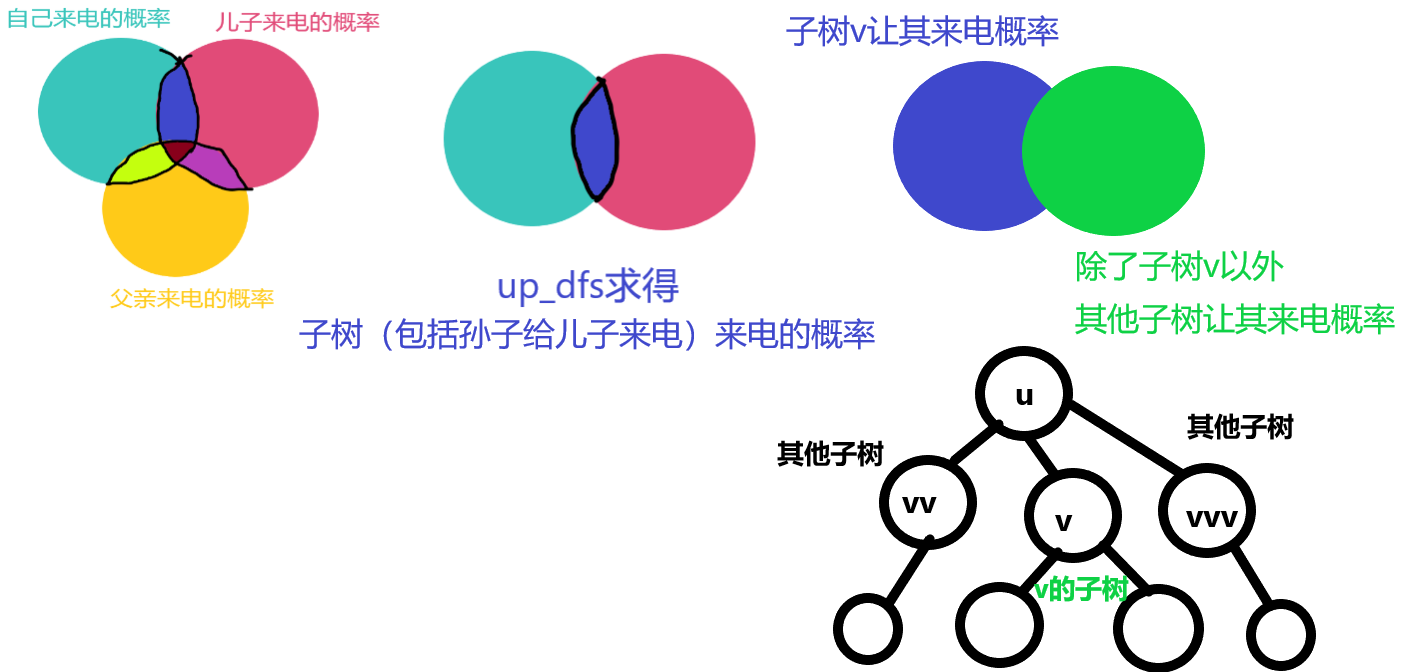
假设节点 \(v\) 没有电，接受父亲节点 \(u\) 的电
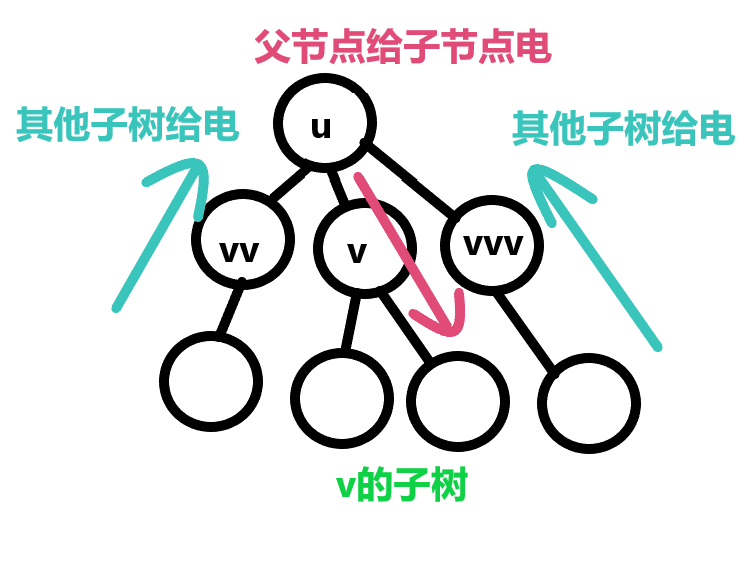
设 \(p_{uv}\) 是节点 \(u\) 除了以节点\(v\)为根的子树以外的子树传入电的概率（包括自身节点 \(u\)），\(p_v\times w_{v,u}\) 是节点 \(v\) 及其子树给节点 \(u\) 传电的概率（包括自身节点 \(v\)），容斥原理得到：
解方程得到
有了这个我们得到父亲来电概率是 \(p_{u,v}\times w{u,v}\)，见上图第一个图的左上角的三圆容斥已经被我们弄成了两圆容斥了，再次容斥
ps：看到上面的倒数第二个公式了嘛，那个有分母的记得分母不为 \(0\) 特判，而且还特别卡精度 \(10^{-8}\)。。
Miku's Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
const int maxn=5e5+50;
const double eps=1e-8;
//1e-6被卡精度Wa95
int n,q[maxn],dep[maxn];
double p[maxn],ans;
int head[maxn<<1],t;
struct edge{
int u,v,w;
int next_;
};edge e[maxn<<1];
il void add_edge(int u,int v,int w){
e[++t].u=u;
e[t].v=v;
e[t].w=w;
e[t].next_=head[u];
head[u]=t;
}
il void input(){
scanf("%d",&n);
int u,v,w;
for(int i=1;i<=n-1;++i){
scanf("%d %d %d",&u,&v,&w);
add_edge(u,v,w);
add_edge(v,u,w);
}
for(int i=1;i<=n;++i){
scanf("%d",&q[i]);
p[i]=q[i]*0.01;
}
}
void up_dfs(int now,int fa){
for(int i=head[now];i;i=e[i].next_){
int to=e[i].v;
if(to==fa) continue;
up_dfs(to,now);
p[now]=p[now]+p[to]*(double)e[i].w/100-p[now]*p[to]*(double)e[i].w/100;
}
}
il bool judge(double a,double b){ //如果a==1表示一定会来电就不要更新啦
if(a-eps<b && a+eps>b) return true;
else return false;
}
void down_dfs(int now,int fa){
ans=ans+p[now];
//更新的是子节点的,现节点直接加
for(int i=head[now];i;i=e[i].next_){
int to=e[i].v;
if(to==fa) continue;
if(judge(p[to]*(double)e[i].w/100,1.0)){
//分母不能为0
down_dfs(to,now);
continue;
}
else{
double puv=(p[now]-p[to]*(double)e[i].w/100)/(1-p[to]*(double)e[i].w/100);
p[to]=p[to]+(puv*(double)e[i].w/100)-puv*(double)e[i].w/100*p[to];
down_dfs(to,now);
}
}
}
int main(){
//freopen("charger3.in","r",stdin);
//freopen("MYOUT.txt","w",stdout);
input();
up_dfs(1,0);
down_dfs(1,0);
printf("%.6lf",ans);
return 0;
}
[HNOI2013] 游走
[HNOI2013] 游走
题目描述
给定一个 \(n\) 个点 \(m\) 条边的无向连通图，顶点从 \(1\) 编号到 \(n\)，边从 \(1\) 编号到 \(m\)。
小 Z 在该图上进行随机游走，初始时小 Z 在 \(1\) 号顶点，每一步小 Z 以相等的概率随机选择当前顶点的某条边，沿着这条边走到下一个顶点，获得等于这条边的编号的分数。当小 Z 到达 \(n\) 号顶点时游走结束，总分为所有获得的分数之和。 现在，请你对这 \(m\) 条边进行编号，使得小 Z 获得的总分的期望值最小。
输入格式
第一行是两个整数，分别表示该图的顶点数 \(n\) 和边数 \(m\)。
接下来 \(m\) 行每行两个整数 \(u,v\)，表示顶点 \(u\) 与顶点 \(v\) 之间存在一条边。
输出格式
输出一行一个实数表示答案，保留三位小数。
样例 #1
样例输入 #1
3 3
2 3
1 2
1 3
样例输出 #1
3.333
提示
样例输入输出 1 解释
边 \((1,2)\) 编号为 \(1\)，边 \((1,3)\) 编号 \(2\)，边 \((2,3)\) 编号为 \(3\)。
数据规模与约定
- 对于 \(30\%\) 的数据，保证 \(n\leq 10\)。
- 对于 \(100\%\) 的数据，保证 \(2\leq n \leq 500\)， \(1 \leq m \leq 125000\)，\(1 \leq u, v \leq n\)，给出的图无重边和自环，且从 \(1\) 出发可以到达所有的节点。
解题：
不好想这道题。
\(O(n^3)\) 贪心+高斯消元做法：
- 考虑每条边的期望次数：
因为这个贡献不是边的编号嘛。
设 \(f_u\) 表示经过点 \(u\) 的期望次数，\(d_u\) 表示点 \(u\) 的出度，有：
显然，某条边的期望经过次数等于这条边连接的两个点的期望经过次数乘下一步走这条边的概率。
2.考虑经过每个点的期望次数：
设 \(E_u\) 表示与点 \(u\) 相连的点集，有：
显然，某个点的期望经过次数等于这个点相连的其他点乘上它们走能够到达该点的边的概率。
但是有两个重要的特例：
-
第 \(1\) 个节点：刚开始就经过，\(f_1=1+\sum_{v \in E_1}\limits \frac{f_v}{d_v}\)。
-
第 \(n\) 个节点：走到这里就结束了，不会再向任何一个点走，所以这个点不能作为别的点的 \(v \in E_u\) 里以至转移，怎么办呢？将 \(f_n\) 设为0。
3.高斯消元求解：
设 \(p_{i,j}\) 是点 \(j\) 到点 \(i\) 的概率。
有：
然而我们的高斯消元全部为加，我们可以将这个 \(p\) 预处理出来的时候就乘上 \(-1.0\)，作为高斯消元的数组 \(a\)。
4.贪心：期望次数多的边给它更小的编号。
没了。（想念滚动数组的每一天）
Miku's Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e2+50,maxm=125050;
int n,m,d[maxn],u[maxm<<1],v[maxm<<1];
int y;
double a[maxn][maxn],g[maxm],ans;
int head[maxm<<1],t;
struct edge{
int u,v,w;
int next_;
};edge e[maxm<<1];
void add_edge(int u,int v){
e[++t].u=u;
e[t].v=v;
e[t].next_=head[u];
head[u]=t;
}
void input(){
scanf("%d %d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d %d",&u[i],&v[i]);
add_edge(u[i],v[i]);
add_edge(v[i],u[i]);
++d[u[i]];
++d[v[i]];
}
}
void builda(){ //构造增广矩阵
for(int u=1;u<n;++u){
for(int i=head[u];i;i=e[i].next_){
int to=e[i].v;
if(to!=n) a[u][to]=-1.0/d[to]; //从v走到u的概率
}
a[u][u]=1;
//f_k的系数为1
}
a[1][n]=1;
//第一个等式等号右边是1
}
void gauss(int n){
for(int i=1;i<=n;++i){
y=i;
while(a[y][i]==0&&y<=n) ++y;
//if(y==n+1){
// cout<<"No Solution";
// return;
//}不可能无解
for(int j=1;j<=n+1;++j){
swap(a[i][j],a[y][j]);
}
double k=a[i][i];
for(int j=1;j<=n+1;++j){
a[i][j]/=k;
}
for(int j=1;j<=n;++j){
if(i!=j){
double ki=a[j][i];
for(int q=1;q<=n+1;++q){
a[j][q]-=ki*a[i][q];
}
}
}
}
}
void solve_edge(){
for(int i=1;i<=m;++i){
g[i]=a[u[i]][n]/d[u[i]]+a[v[i]][n]/d[v[i]];
}
sort(g+1,g+1+m);
}
int main(){
input();
builda();
gauss(n-1);
/*for(int i=1;i<=n-1;++i){
for(int j=1;j<=n;++j){
printf("%.2lf ",a[i][j]);
}
printf("\n");
}*/
solve_edge();
for(int i=1;i<=m;++i){
//升序排序,贡献小的边编号最大
ans=ans+g[i]*(m-i+1);
}
printf("%.3lf",ans);
return 0;
}
