题目描述

题目描述
FGD想从成都去上海旅游。在旅途中他希望经过一些城市并在那里欣赏风景，品尝风味小吃或者做其他&的有趣的事情。经过这些城市的顺序不是完全随意的，比如说FGD不希望在刚吃过一顿大餐之后立刻去下一个城市登山，而是希望去另外什么地方喝下午茶。幸运的是,FGD的旅程不是既定的，他可以在某些旅行方案之间进行选择。由于FGD非常讨厌乘车的颠簸，他希望在满足他的要求的情况下，旅行的距离尽量短，这样他就有足够的精力来欣赏风景或者是泡MM了^_. 整个城市交通网络包含N个城市以及城市与城市之间的双向道路M条。城市自1至N依次编号，道路亦然。没有从某个城市直接到它自己的道路，两个城市之间最多只有一条道路直接相连，但可以有多条连接两个城市的路径。任意两条道路如果相遇，则相遇点也必然是这N个城市之一，在中途，由于修建了立交桥和下穿隧道，道路是不会相交的。每条道路都有一个固定长度。在中途，FGD想要经过K(K<=N-2)个城市。成都编号为1，上海编号为N,而FGD想要经过的N个城市编号依次为2,3,…,K+1.

举例来说，假设交通网络如下图。

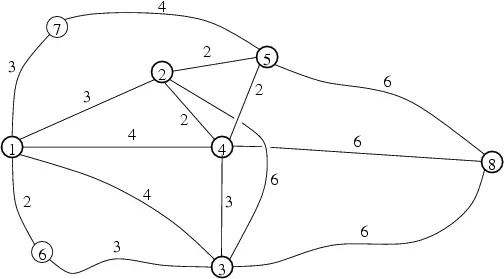
FGD想要经过城市2,3,4,5，并且在2停留的时候在3之前，而在4,5停留的时候在3之后。那么最短的旅行方案是1-2-4-3-4-5-8,总长度为19。注意FGD为了从城市2到城市4

可以路过城市3,但不在城市3停留。这样就不违反FGD的要求了。并且由于FGD想要走最短的路径，因此这个方案正是FGD需要的。

输入格式
第一行包含3个整数N(2<=N<=20000),M(1<=M<=200000),K(0<=K<=20),意义如上所述。以下M行，每行包含3个整数X，y，z，(1<=x，y<=n，0<z<=1000)；

接下来一行，包含一个整数q，表示有q个限制条件(0<=q<n)。以下q行，每行两个整数f，l(1<=l，f<=n)，表示在f停留的时候要在l之前。

输出格式
只包含一行，包含一个整数，表示最短的旅行距离。

样例
样例输入

样例输出

提示

对于 \(100\%\) 的数据，满足：

\(2\le n\le2\times10^4\)
\(1\le m\le2\times10^5\)
\(0\le k\le\min(20, n-2)\)
\(1\le p_i<q_i\le n\)
\(1\le l_i\le 10^3\)
\(2\le r_i, s_i\le k+1, r_i\not=s_i\)
保证不存在重边且一定有解。

题意概括

这道题题目描述好长（

有 \(N\) 个点 \(M\) 条边的无向图，不存在重边与自环。

要求寻找一条从 \(1\) 到 \(n\) 的最短路径，而且还必须经过 \(2\sim K+1\) 并且按照 \(g\) 给出的要求停留在这些城市。

而且你可以选择不停留，类似于就是样例图中，我们到从 \(2\) 到 \(3\) 的时候经过了城市 \(4\)，但是我们选择不停留，这样的话就满足了 \(2\sim 3-4\) 的停留顺序。

然后就是这个题目有一个很重要的隐藏条件，就是如果我们没有要求必须停留的点就没有所谓的停留顺序限制，也就是说 \(k==0\) 时 \(g==0\)，直接 dijkstra 即可

思路历程

私货：初音未来什么时候来中国~~开演唱会~~旅游啊（

1.找最短路

找最短路，没有负数和重边、自环，我想到了\(dijkstra\)

所以先粘贴一下我的与众不同的\(dijkstra\)板子，用了\(pair\)

粘贴的香甜的黄油这道题（）

已经忘光力（

Miku's dijkstra code

int head[maxm<<1],t;
struct edge{
	int u,v,w;
	int next_;
};edge e[maxm<<1];
void add_edge(int u,int v,int w){
	e[++t].u=u;
	e[t].v=v;
	e[t].w=w;
	head[u]=t;
}
int dis[maxn];
bool judge[maxn];
typedef pair<int,int> strack;

void search_dijkstra(int x){		//x是终点牧场的下标
	memset(judge,false,sizeof judge);	//将judge初始化 
	memset(dis,0x3f,sizeof dis);	//将距离定义为无穷大
	dis[x]=0;						//终点距离为0
	
	priority_queue<strack,vector<strack>,greater<strack> >heap;
	//建立一个小根堆
	while(!heap.empty()){			//小根堆初始化 
		heap.pop();
	}
	heap.push({0,x});				//终点牧场入堆
	while(!heap.empty()){
		strack t=heap.top();
		heap.pop();
		int temp=t.second,distance=t.first;
		//temp是节点编号,distance是节点距离
		if(judge[temp]==true)	continue;//如果节点被访问过则跳过
		judge[temp]=true;
		for(int i=head[temp];i!=0;i=next[i]){
			int j=to[i];			//取出节点编号
			if(distance+w[i]<dis[j]){ 
				dis[j]=distance+w[i];
				heap.push({dis[j],j});
			} 
		} 
	}
}

2.设计状态

所以先考虑设置状态。

刚刚的题意概括，已经说了，显然是有三种状态：没经过、经过但未停留、停留。

没经过与经过的区别在于是否累加我们的 \(dis\)，而经过与停留的区别在于我们的限制条件判断

然而我们的停留是属于经过状态的，并且经过可以是多次的，但停留我们只有一次，所以我们设计状态应该在停留上下手。

我们设置 \(f_{i,s,j}\) 作为dp数组，其中 \(i\) 是停留的点的数量，通过从 \(i-1\) 到 \(i\) 的转移满足 \(2\sim k+1\) 这些点都经过，\(s\) 则是当前的状态，当前状态停留点数一定为 \(i\) 即有 \(i\) 个 \(1\)，\(j\) 是当前停留的点

转移方程看起来就比较简单：

\[\begin{aligned} f_{i,s,j}=min(f_{i,s,j},f_{i-1,去掉j点停留的状态s,上一次停留点q}+diss_{q,j}) \end{aligned} \]

这样的话我们需要初始化 \(f_1\)，作为第一个停留的点，必须没有任何限制条件，初始值就是到起点 \(1\) 的距离

最后的答案就应该在 \(f_n\) 中寻找最短路。

3.优化空间

这个时候我们发现无法通过洛谷的数据，原因是臭名昭著的：

64MB空间限制！

那么我们考虑对空间进行优化：

1.滚动数组

我们设计状态转移时发现两个问题：

我们的状态在查询时，只有最终状态（停留点数为 \(k\)）对我们有用。

我们在状态转移时，只有上一个状态对现在的状态有用。（对比炮兵阵列亲切许多）

那么严格意义上来说，我们只需要两个状态：当前状态，上一个状态。

那么我们将 \(f\) 数组的第一维改变为 \(cur\)，只有 \(0\) 和 \(1\) 两种状态，\(cur\) 表示当前状态，\(cur异或1\) 表示上一个状态，不断更新，最后在 \(cur\) 中寻找我们的答案即可

2.设置索引

设计状态时，我们提到，当前状态的 \(s\) 其停留点数一定等于 \(i\)，那么我们其实有非常多的空间都是非法状态。

非法状态对我们没有用我们碰都不会碰，所以我们将其优化。

如何优化呢？类似于离散化，但是我们需要的不是“大小关系”，而是该状态的索引 \(pbelong\)。

设置一个容器，将停留点数相同的状态放进一个容器里，\(pbelong\) 就等于容器的 \(size()-1\)，类似于数组的下标。

优化总结

我们设置 \(f_{cur,i,j}\) 作为dp数组，其中 \(cur\) 是当前状态，只有 \(0\) 和 \(1\)，通过从上一个状态的转移满足 \(2\sim k+1\) 这些点都经过，而枚举状态时要求满足所有的限制条件

\(i\) 用来找到状态，\(j\) 则是上一个停留的点

\[\begin{aligned} f_{cur,i,j}=min(f_{cur,i,j},f_{cur异或1,i的二进制去掉停留点j,q}+diss_{q,j}) \end{aligned} \]

这样我们的空间复杂度就从\(k\times 2^k\times k\)优化到了\(2\times \dbinom{20}{10}\times k\)

ps:\(\dbinom{20}{10}\) 等于 \(184756\)，所以代码数组开 \(184757\)。

代码实现

(ps：把注释删掉，不要使用long long，可以通过洛谷的测试)

Miku's Code

#include<bits/stdc++.h>
using namespace std;

const int maxn=2e4+50,maxm=2e5+50,maxk=25;
typedef long long intx;
int n,m,k;
int g,limits[maxk];
int belong[maxk],cur;
int f[2][184757][maxk];
//f[cur][i][j],cur表示当前状态,i表示状态在容器中的索引,j表示上一个停留的点

int sum[(1<<maxk)+50],pbelong[(1<<maxk)+50];
vector <int> p[maxk];
/*
sum[s]数组表示停留状态中停了几个点,也就是有几个1,通过递推获得
pbelong[s]是s状态在容器里的索引
p[sum[s]]表示停留了sum[s]个点的现在的状态
*/

int head[maxm<<1],t;
struct edge{
	int u,v,w;
	int next_;
};edge e[maxm<<1];
void add_edge(int u,int v,int w){
	e[++t].u=u;
	e[t].v=v;
	e[t].w=w;
	e[t].next_=head[u];
	head[u]=t;
}
int dis[maxn],dist[maxk][2],diss[maxk][maxk];
/*
dis[]是dijkstra相关数组
dist[i][0]表示点1到点i的最短路距离,[1]表示点i到点n的最短路距离
diss[i][j]表示二进制的第j个点(点的编号为j+2)到点的编号为i的第i个点的距离
*/
bool judge[maxn];
typedef pair<int,int> strack;

void input(){
	scanf("%d %d %d",&n,&m,&k);
	int p,q,l;
	for(int i=1;i<=m;++i){
		scanf("%d %d %d",&p,&q,&l);
		add_edge(p,q,l);
		add_edge(q,p,l);
	}
	if(k!=0){							//只有k不等于0时,才可能有限制条件
		scanf("%d",&g);
		int r,s;
		for(int i=1;i<=g;++i){
			scanf("%d %d",&r,&s);
			limits[s-2]|=(1<<(r-2));
			/*
			我们将2~k+1这些必须停留的点设置状态,统一左移2位为0~k-1,与二进制数保持一致
			'|'表示只有两个位置都为0时,结果为0,这样我们得到的状态就是s城市停留之前的状态
			*/
		}
	}
}

void dijkstra(int x){
	memset(dis,0x3f,sizeof(dis));
	memset(judge,false,sizeof(judge));
	dis[belong[x]]=0;
	priority_queue<strack,vector<strack>,greater<strack> >heap;
	while(!heap.empty()){
		heap.pop();
	}
	heap.push({0,belong[x]});
	while(!heap.empty()){
		strack s=heap.top();
		heap.pop();
		int temp=s.second,distance=s.first;
		if(judge[temp]==true)	continue;
		judge[temp]=true;
		for(int i=head[temp];i;i=e[i].next_){
			int j=e[i].v;
			if(distance+e[i].w<dis[j]){
				dis[j]=distance+e[i].w;
				heap.push({dis[j],j});
			}
		}
	}
	dist[x][0]=dis[1],dist[x][1]=dis[n];
	for(int i=0;i<k;++i){
		diss[x][i]=dis[belong[i]];
	}
}

inline int lowbit(int x){
	return x&(-x);
}

void pre(){
	for(int i=0;i<k;++i){
			belong[i]=i+2;
		}
		for(int s=1;s<(1<<k);++s){
			sum[s]=sum[s&(~(lowbit(s)))]+1;
			/*
			从1开始,0的话位运算会出现错误
			(0的'~'返回值为-1)
			lowbit(x)得到最后一个1
			'~'表示取反,'&'只有同为1才返回1
			所以这样我们就得到了停留了多少个点
			*/
			p[sum[s]].push_back(s);
			pbelong[s]=p[sum[s]].size()-1;
			/*
			pbelong[s]是s状态的一个索引,因为s是刚刚放进容器里的,所以它在容器里的位置一定是p[sum[s]].size()-1
			*/
		}
		memset(f,0x3f,sizeof(f));
		for(int i=0;i<k;++i){
			dijkstra(i);
			if(!limits[i])	f[cur][pbelong[1<<i]][i]=dist[i][0];
		}
}

void work(){
	cur=0;
	for(int i=2;i<=k;++i){
		int len=p[i].size();
		cur^=1;					//最后一位取反,f数组第一位状态只有0与1
		memset(f[cur],0x3f,sizeof(f[cur]));
		for(int e=0;e<len;++e){
			int s=p[i][e];
			for(int j=0;j<k;++j){
				
				if( (s&(1<<j)) && ( ( limits[j] & (s&(~(1<<j))) )==limits[j]) ){
					/*
					我们枚举停留了i个点,最后一个被停留的点是点j,目的是判断合法状态
					len表示停留了i个点的状态总数
					那么枚举s就表示停留了i个点的各个状态
					一定停留了第j个点所以s&(1<<j)==true
					要求满足点j停留的限制条件所以limits[j] &(s&(~(1<<j))==limits[j]
					其中,s&(~(1<<j))表示j停留之前的状态
					该状态与限制状态取&应该为限制状态
					*/
					for(int q=0;q<k;++q){
						if(j!=q	&&	(s&(1<<q)) ){
							f[cur][e][j]=min(f[cur][e][j],f[cur^1][pbelong[s&(~(1<<j))]][q]+diss[q][j]);
							//cout<<"###"<<i<<' '<<(cur^1)<<' '<<pbelong[s&(~(1<<j))]<<' '<<q<<endl;
							//cout<<"###"<<f[cur^1][pbelong[s&(~(1<<j))]][q]<<' '<<"###"<<diss[q][j]<<endl;
						}
						/*
						转移状态,q是枚举的上一个停留点
						*/
					}
				}
			}
		}
	}
}

int main(){
	input();
	if(k==0){
		belong[1]=1;			//没有前置条件,直接dijkstra
		dijkstra(1);
		printf("%d\n",dis[n]);
		return 0;
	}
	pre();
	work();
	int ans=0x3f3f3f3f;
	for(int i=0;i<k;++i){
		ans=min(ans,f[cur][0][i]+dist[i][1]);
		/*
		为什么第二维的索引是0？
		因为我们的cur表示的是当前状态,而当前状态的所有点已经从上一状态转移
		也就是说,我们现在的状态已经经过了2~k+1所有点并且满足了所有的限制条件
		现在我们这个状态cur中,只有一个状态就是全部停留,其索引是0
		*/
	}
	printf("%lld\n",ans);
	return 0;
}

posted @ 2023-07-03 10:23 Sonnety 阅读(156) 评论(5) 编辑收藏举报

刷新页面返回顶部

$\mathcal{Namanyi\ Bruce}$

如果说，生命的脚步终有一天被时间的尘埃掩埋，那么我们就永远不能停下脚步。

【题解】旅游景点 Tourist Attractions

题目链接