【题解】P2973 [USACO10HOL] Driving Out the Piggies G 臭气弹/驱逐猪猡

题目链接
题目：
奶牛们建立了一个随机化的臭气炸弹来驱逐猪猡。猪猡的文明包含1到N (2 <= N <= 300)一共N个猪城。这些城市由M (1 <= M <= 44,850)条由两个不同端点A_j和B_j (1 <= A_j<= N; 1 <= B_j <= N)表示的双向道路连接。保证城市1至少连接一个其它的城市。

一开始臭气弹会被放在城市1。每个小时（包括第一个小时），它有P/Q (1 <= P <=1,000,000; 1 <= Q <= 1,000,000)的概率污染它所在的城市。如果这个小时内它没有污染它所在的城市，那麽它随机地选择一条道路，在这个小时内沿着这条道路走到一个新的城市。可以离开这个城市的所有道路被选择的概率均等。

因为这个臭气弹的随机的性质，奶牛们很困惑哪个城市最有可能被污染。给定一个猪猡文明的地图和臭气弹在每个小时内爆炸的概率。计算每个城市最终被污染的概率。

如下例，假设这个猪猡文明有两个连接在一起的城市。臭气炸弹从城市1出发，每到一个城市，它都有1/2的概率爆炸

                         1--2 

可知下面这些路径是炸弹可能经过的路径（最后一个城市是臭气弹爆炸的城市）：

1: 1
2: 1-2
3: 1-2-1
4: 1-2-1-2
5: 1-2-1-2-1
...

要得到炸弹在城市1终止的概率，我们可以把上面的第1，第3，第5……条路径的概率加起来，（也就是上表奇数编号的路径）。上表中第k条路径的概率正好是，也就是必须在前k-1个回合离开所在城市（每次的概率为1 - 1/2 = 1/2）并且留在最后一个城市（概率为1/2）。

所以在城市1结束的概率可以表示为1/2 + (1/2)^3 + (1/2)^5 + ...。当我们无限地计算把这些项一个个加起来，我们最后会恰好得到2/3，也就是我们要求的概率，大约是0.666666667。这意味着最终停留在城市2的概率为1/3，大约为0.333333333。

你将会在你前50次提交的时候得到部份测试数据反馈。

题目名称: dotp

输入格式：
第1行: 四个由空格隔开的整数: N, M, P, 和 Q
第2到第M+1行: 第i+1行用两个由空格隔开的整数A_j和B_j表示一条道路。

输出格式：
第1到第N行: 在第i行，用一个浮点数输出城市i被摧毁的概率。误差不超过10^-6的答案会被接受（注意这就是说你需要至少输出6位有效数字使得答案有效）。

样例输入：

 2 1 1 2
 1 2

样例输出：

0.666666667
0.333333333

---

私货：初音未来：没活了给大家唱首歌吧
题意概括：
给出一个n个点、m条边的无向图，在节点1有一枚炸弹。炸弹在每个节点都有\({p\over q}\)的概率爆炸，1-\({p\over q}\)的概率转入其他节点，要求输出每个点的爆炸概率。

思路分析
一个无向图，联系高斯消元的矩阵，很容易想到邻接链表。
通过邻接链表我们就将一个图转换成了一个矩阵。
而对于每一个点，都有\({p\over q}\)的概率爆炸。
而除了炸弹所在初始点为点1外，所有的炸弹都是转入来的
我们设第i个点的转入概率是 \(x_i\)

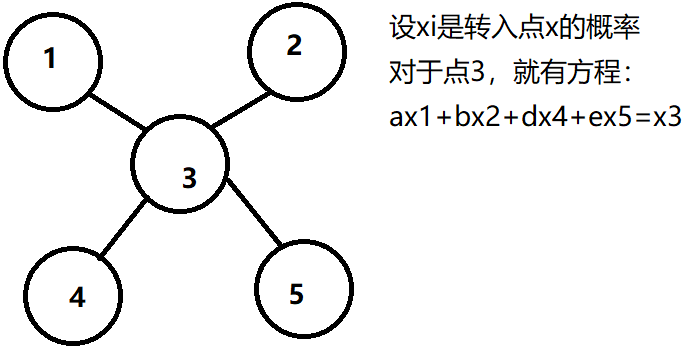
对图的解释：以\(x_1\)为例子，\(x_1\)是点1的转入概率，而它的系数a就是\(x_1\)转入\(x_3\)的概率，a=(1-\({p\over q}\))*\({1\over d_1}\)（\(d_1\)是点1的入度）
而此方程可以将x3左移过去就有了矩阵：
a b -1 d e | 0
同理但特殊的，对于点1，最初炸弹就在这里，我们在等式左边加1，可以移动到等式右边去
得到矩阵：
-1 0 c 0 0 | -1
(因为节点1只和3相连所以\(x_2\)、\(x_4\)、\(x_5\)的系数都是0)
我们得到了矩阵，就可以运用高斯消元得到未知数 \(x_i\)的值
该值乘上\({p\over q}\)就得到了在该点爆炸的概率。
注意：
p/q应是double类型

Miku's Code:

#include<bits/stdc++.h>
using namespace std;

const int maxn=350;
const int eps=1e-8;

int n,m,p,q;
double k;
int d[maxn];
double a[maxn][maxn];
bool cont[maxn][maxn]；

void input(){						//输入
	scanf("%d%d%d%d",&n,&m,&p,&q);
	int A,B;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&A,&B);
		cont[A][B]=true;cont[B][A]=true;
		++d[A];++d[B];
	}
}

void change(){						//转化出矩阵
	a[1][n+1]=-1;
	k=(double)p/q;
	for(int i=1;i<=n;++i){
		a[i][i]=-1;
		for(int j=1;j<=n;++j){
			if(cont[i][j]==true){
				a[i][j]=(1-k)/d[j];
			}
		}
	}
}

void try_(){						//调试代码
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n+1;++j){
			if(j==n+1)	cout<<"| ";
			cout<<a[i][j]<<' ';
		}
		cout<<endl;
	}
}

void work(){						//高斯约旦消元板子
	for(int i=1;i<=n;++i){
		int y=i;
		while(fabs(a[y][i])<=fabs(eps)&&y<=n)	++y;
		for(int j=1;j<=n+1;++j){
			swap(a[i][j],a[y][j]);
		}
		double k=a[i][i];
		for(int j=1;j<=n+1;++j){
			a[i][j]/=k;
		}
		for(int j=1;j<=n;++j){
			if(i!=j){
				double ki=a[j][i];
				for(int q=1;q<=n+1;++q){
					a[j][q]-=ki*a[i][q];
				}
			}
		}
	}
}

int main(){
	input();
	change();
	//try_();
	work();
	//try_();
	for(int i=1;i<=n;++i){
		printf("%.6lf\n",a[i][n+1]*k);
	}
	return 0;
}

注：本人不是Miku黑，整活部分如有冒犯请见谅。
QAQ