【题解】SDOI 2011 染色

题目链接

题目：

　　给定一棵有 n 个节点的无根树和 m 个操作，操作共两类。

1. 将节点 a 到节点 b 路径上的所有节点都染上颜色；

2. 询问节点 a 到节点 b 路径上的颜色段数量，连续相同颜色的认为是同一段，例如 112221 由三段组成：11 、 222、1。

请你写一个程序依次完成操作。

输入格式

第一行包括两个整数 n，m表示节点数和操作数；

第二行包含 n 个正整数表示 n 个节点的初始颜色；

接下来若干行包含两个整数 x 和 y，表示 x 和 y 之间有一条无向边；

接下来若干行每行描述一个操作：

• C a b c 表示这是一个染色操作，把节点 a 到节点 b 路径上所有点（包括 a 和 b）染上颜色；

• Q a b 表示这是一个询问操作，把节点 a 到节点 b 路径上（包括 a 和 b）的颜色段数量。

输出格式

对于每个询问操作，输出一行询问结果。

样例输入：

6 5
2 2 1 2 1 1
1 2
1 3
2 4 
2 5 
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5

样例输出：

3
1
2

私货：初音未来的应援色是#39C5BB

---

题意概括：
给一棵树，对其特定区间修改值，求某一区段连续相同值区块的个数。

---

做题思路：
将树改成一条序列的话，这个题目就会成为：
一段序列，修改区间，求一段区间的连续相同序列个数。
实现方法：区间修改线段树+树链剖分

递归到终点的时候每一段只有一个颜色，故push_up的过程就是序列合并的过程

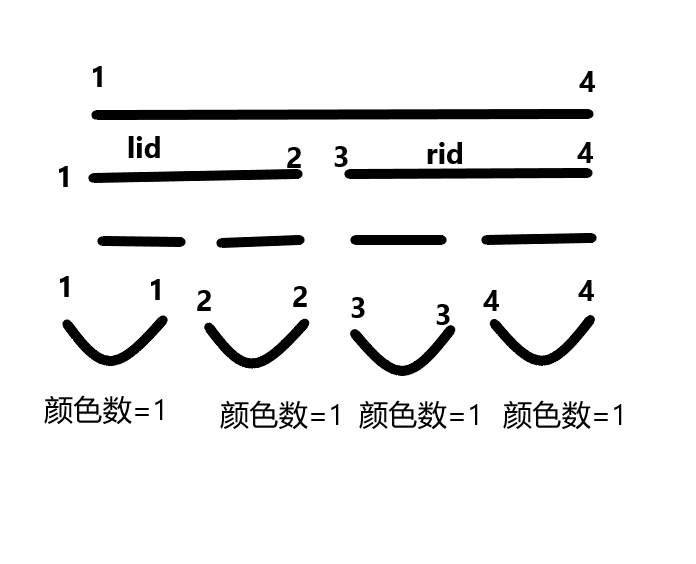
对于建树，我们向下递归后push_up()
(注:lc是序列最左端的颜色，rc是最右端的颜色）

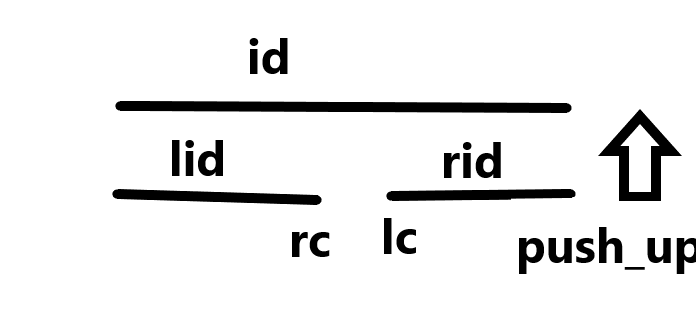
我们将两个小区间push_up合并成大区间时，合并前两个区间的序列就变成了一个区间
所以如果 tr[lid].lc==tr[rid].rc，那么合并前原本算成两段颜色段的区间就在合并后变成了一个区间段，需要--颜色段计数
易得：

void push_up(int id){
	tr[id].lc=tr[lid].lc;
	tr[id].rc=tr[rid].rc;
	tr[id].ccnt=tr[lid].ccnt+tr[rid].ccnt;		//ccnt表示颜色数
	if(tr[lid].rc==tr[rid].lc)	--tr[id].ccnt;
}

---

相似的，push_down区间修改颜色：
整个区间都变为一个颜色。

void push_down(int id){
	tr[lid].lazy=tr[rid].lazy=tr[id].lazy;
	tr[lid].lc=tr[rid].lc=tr[lid].rc=tr[rid].rc=tr[id].lazy;
	tr[lid].ccnt=tr[rid].ccnt=1;
	tr[id].lazy=0;
}

---

那么只要是类似于合并的都要--ccnt：
树链剖分是较深的点向上跳

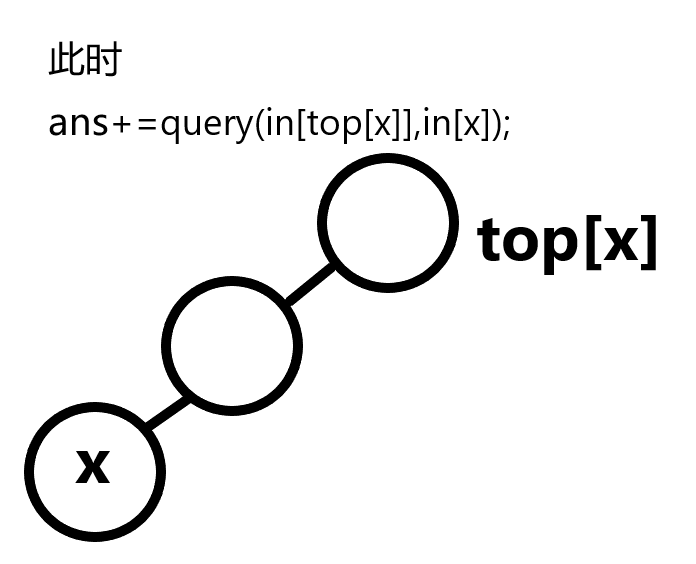
接下来x=fa[top[x]]跳跃时

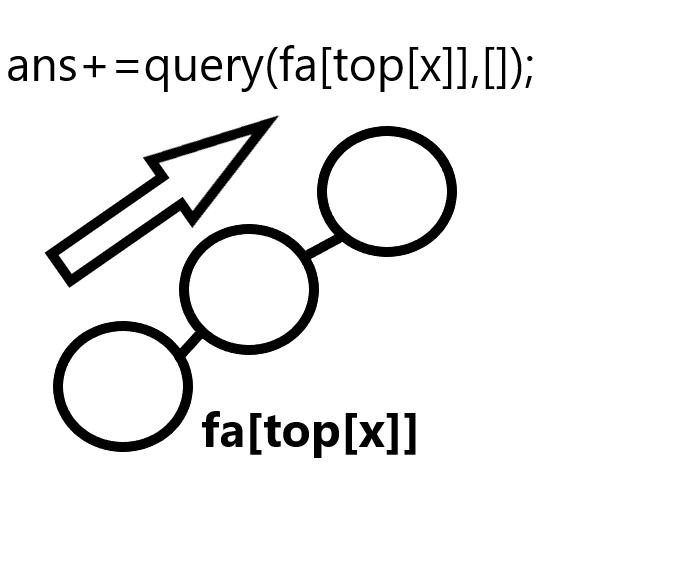
这何尝不是一种合并呢（笑）
第一个区间是x————top[x]
第二个区间是fa[top[x]]————top[]
两个区间合并时
如果top[x]==fa[top[x]]
两个点合并前算两个颜色段，合并后算一个颜色段！
--ccnt；
易得：

//find_col是寻找top[x]和fa[top[x]]的颜色的，代码类似于单点查询
int find_col(int id,int l,int r,int x){
	if(l==r)	return tr[id].lc;
	if(tr[id].lazy)	push_down(id);
	int mid=(l+r)>>1;
	if(x<=mid)	return find_col(lid,l,mid,x);
	if(x>mid)	return find_col(rid,mid+1,r,x);
}
 
int get(int x,int y){
	int fx=top[x],fy=top[y],ans=0;
	while(fx!=fy){
		if(dep[fx]<dep[fy])	swap(x,y),swap(fx,fy);
		ans+=query(1,1,n,in[fx],in[x]);
		if(find_col(1,1,n,in[fx])==find_col(1,1,n,in[myf[fx]]))	--ans;
		x=myf[fx];fx=top[x];
	}
	if(dep[x]<dep[y])	swap(x,y);
	ans+=query(1,1,n,in[y],in[x]);
	return ans;
}

注意：
push_down下放标记必须在if(lazy)的条件下，否则不该修改的全都被修改成了颜色0

Miku's code:

#include<bits/stdc++.h>
using namespace std;
 
#define lid	id<<1
#define rid id<<1|1
const int maxn=100500;
 
int root;
int n,m,q,a[maxn];
int in[maxn],my_in[maxn],dep[maxn],myf[maxn],tim;
int sonum[maxn],hson[maxn],top[maxn];
 
int t,f[maxn<<1];
struct edge{
	int u,v,next_;
};edge e[maxn<<1];
void add_edge(int u,int v){
	e[++t].u=u;
	e[t].v=v;
	e[t].next_=f[u];
	f[u]=t;
}
struct tree{
	int id,l,r,lc,rc;
	int lazy;
	int ccnt;
};tree tr[maxn<<2];
 
void push_up(int id){
	tr[id].lc=tr[lid].lc;
	tr[id].rc=tr[rid].rc;
	tr[id].ccnt=tr[lid].ccnt+tr[rid].ccnt;
	if(tr[lid].rc==tr[rid].lc)	--tr[id].ccnt;
}
 
void push_down(int id){
	tr[lid].lazy=tr[rid].lazy=tr[id].lazy;
	tr[lid].lc=tr[rid].lc=tr[lid].rc=tr[rid].rc=tr[id].lazy;
	tr[lid].ccnt=tr[rid].ccnt=1;
	tr[id].lazy=0;
}
 
void build_tree(int id,int le,int ri){
	tr[id].l=le,tr[id].r=ri;
	if(le==ri){
		tr[id].lc=tr[id].rc=my_in[le];
		tr[id].ccnt=1;
		return;
	}
	int mid=(le+ri)>>1;
	build_tree(lid,le,mid);
	build_tree(rid,mid+1,ri);
	push_up(id);
}
 
void update(int id,int l,int r,int x,int y,int col){
	if(y<l||x>r)	return;
	if(x<=l&&r<=y){
		tr[id].lc=col=tr[id].rc=col;
		tr[id].ccnt=1;
		tr[id].lazy=col;
		return;
	}
	int mid=(l+r)>>1;
	if(tr[id].lazy)	push_down(id);
	if(x<=mid)	update(lid,l,mid,x,y,col);
	if(y>mid)	update(rid,mid+1,r,x,y,col);
	push_up(id);
}
 
int query(int id,int l,int r,int x,int y){
	if(x>r||y<l)	return 0;
	if(x<=l&&r<=y){
		return tr[id].ccnt;
	}
	int mid=(l+r)>>1,ans=0;
	if(tr[id].lazy)	push_down(id);
	ans=query(lid,l,mid,x,y)+query(rid,mid+1,r,x,y);
	if(x<=mid&&mid<y&&tr[lid].rc==tr[rid].lc)	--ans;
	return ans;
}
 
void dfs(int now,int fa){
	myf[now]=fa;
	dep[now]=dep[fa]+1;
	sonum[now]=1;
	for(int i=f[now];i;i=e[i].next_){
		int to=e[i].v;
		if(to==fa)	continue;
		dfs(to,now);
		sonum[now]+=sonum[to];
		if(sonum[to]>sonum[hson[now]]){
			hson[now]=to;
		}
	}
}
 
void dfs_plus(int now,int topp){
	top[now]=topp;
	in[now]=++tim;
	my_in[tim]=a[now];
	if(!hson[now])	return;
	dfs_plus(hson[now],topp);
	for(int i=f[now];i;i=e[i].next_){
		int to=e[i].v;
		if(to!=hson[now]&&to!=myf[now]){
			dfs_plus(to,to);
		}
	}
}
 
int find_col(int id,int l,int r,int x){
	if(l==r)	return tr[id].lc;
	if(tr[id].lazy)	push_down(id);
	int mid=(l+r)>>1;
	if(x<=mid)	return find_col(lid,l,mid,x);
	if(x>mid)	return find_col(rid,mid+1,r,x);
}
 
int get(int x,int y){
	int fx=top[x],fy=top[y],ans=0;
	while(fx!=fy){
		if(dep[fx]<dep[fy])	swap(x,y),swap(fx,fy);
		ans+=query(1,1,n,in[fx],in[x]);
		if(find_col(1,1,n,in[fx])==find_col(1,1,n,in[myf[fx]]))	--ans;
		x=myf[fx];fx=top[x];
	}
	if(dep[x]<dep[y])	swap(x,y);
	ans+=query(1,1,n,in[y],in[x]);
	return ans;
}
 
void solve(int x,int y,int col){
	int fx=top[x],fy=top[y];
	while(fx!=fy){
		if(dep[fx]<dep[fy])	swap(x,y),swap(fx,fy);
		update(1,1,n,in[fx],in[x],col);
		x=myf[fx];fx=top[x];
	}
	if(dep[x]<dep[y])	swap(x,y);
	update(1,1,n,in[y],in[x],col);
}
 
void input(){
	root=1;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i){
		scanf("%d",&a[i]);
	}
	int A,B;
	for(int i=1;i<=n-1;++i){
		scanf("%d%d",&A,&B);
		add_edge(A,B);
		add_edge(B,A);
	}
	dfs(1,0);
	dfs_plus(1,1);
	build_tree(1,1,n);
}
 
int main(){
	input();
	char inn[5];
	int A,B,C;
	for(int i=1;i<=m;++i){
		scanf("%s",&inn);
		if(inn[0]=='C'){
			scanf("%d%d%d",&A,&B,&C);
			solve(A,B,C);
		}
		else{
			scanf("%d%d",&A,&B);
			printf("%d\n",get(A,B));
		}
	}
	return 0;
}

---

做题感悟：
树链剖分板子适合查点权。
在不同链上的x和y最后会到达下图状态：

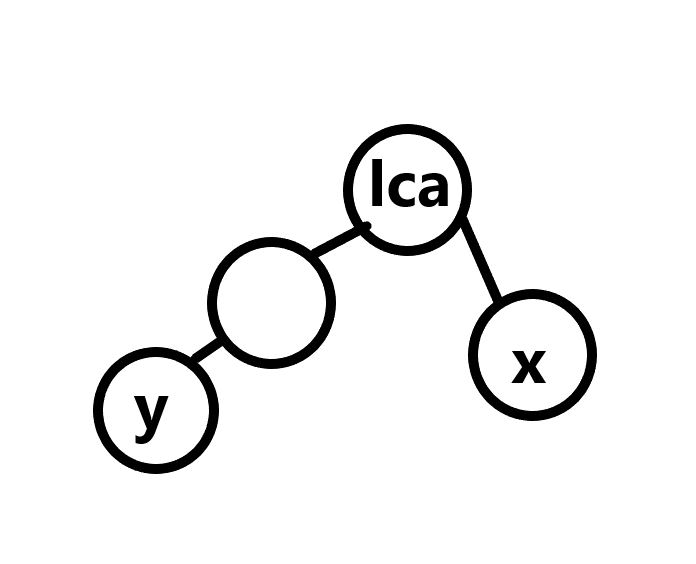
此时x=fa[top[x]]会直接跳到lca
再查询query（in[x],in[y])
这告诉我们：
1.在同一链上较浅的点是lca
2.树链剖分板子不稍加修改的话只能查询点权
（下放边权的题：COGS 1672难存的情缘,这里不进行赘述）

---

注：本人不是Miku黑，整活内容如有不适请见谅
QAQ