坐标及其变换的详解

~ 引入齐次坐标的好处有两个:一个是提供了用矩阵运算吧二维、三维甚至高维空间中的一个点集从一个坐标系变到另一个坐标系的有效方法。第二个好处是可以表示无穷点（这是非齐次坐标系无法做到的）

1.二维空间中的一个点是用二元组表示的。我们可以增加一个额外的坐标得到三元组，同时我们声明这是同一个点。这看起来完全无害，因为我们可以很简单地通过增加或者删除最后一个坐标值来在两种表示方式之间来回切换。现在，有一个很重要的问题是：最后一个坐标为什么需要是1？毕竟，另外两个数字没有这样的限制呀。比方说。在这里，我们要再给出一个定义，即当k非零时，所有形如的三元组都表示同一个点，比如和就表示同一个点。由此我们就可以引出齐次坐标的定义，即给定一个二维点，那么形如的所有三元组就都是等价的，它们就是这个点的齐次坐标。对每一个齐次坐标，我们只要把它除以三元组中的第三个数，即可得到原始的二维点坐标（这就是@祝文祥的答案中所说的同比收缩的一个例子）。不过我觉得，从字面上来看，齐次坐标这个叫法还是不那么形象，不过看看和齐次对应的英文单词homogeneous，我们会发现这个词有时还会被翻译成“同质”，表示某一类东西拥有一些相同的性质，这么来看的话，还是挺形象的吧。

2.需要再次注意的是这里的k是非零的，那么如果会怎样？因为除数不能为的缘故，所以似乎没有任何二维点是和对应的。事实上，就是无穷远处的点。以前，我们用是无法描述二维平面上的无穷远点，但当我们引入齐次坐标之后，就可以用来表示无穷远点了。这就是引入齐次坐标的一个好处。对于（a，b，h），当h->0时,表示ax+by=0的直线,即在y=-(a/b)x上的连续点[x,y]逐渐趋于无穷远点,但斜率不变。

 

~ 坐标的线性变换

“线性变换”(Linear Transformation)同样是计算机视觉和图形学中经常用到的东西。通常，我们会用一个矩阵来表示一个线性变换，对于二维空间中的线性变换，我们经常用3x3的矩阵来表示。当给定一个线性变换矩阵之后，我们把它和一个齐次坐标一乘就可以得到经过变换后的齐次坐标了。

那么为什么我们要管这种变换叫线性变换而不是弯性变换呢？这里抛开线性的数学定义不说，线性变换有一个重要的性质，非常形象地表达了这一概念，即保共线性（我记不清是不是叫这个名字了，望指正）。具体地说就是，在线性变换之前处于同一条直线上的3个点，经过线性变换之后必定还处于同一条直线上。换句话说，如果你画了一条直线，这条直线在经过线性变换之后它必定还是一条直线。

所以说，线性变换最喜欢直线了，除了直线以外的东西，比如角，在经过线性变换之后可能就完全不一样了，此外，还有长度、面积、平行等等，线性变换都不喜欢，不保证它们在变换之后还能维持原样。

 

~ 坐标的投影变换

投影变换指的是物体与投影面上的像之间的变换,是将三维模型显示到二维视图上，如下图所示，投影前的面和投影后的面不是同一个面。
　　

1.正交投影:投影线垂直于投影面的投影属于正交投影,能够保持距离和角度相对大小的不变

 

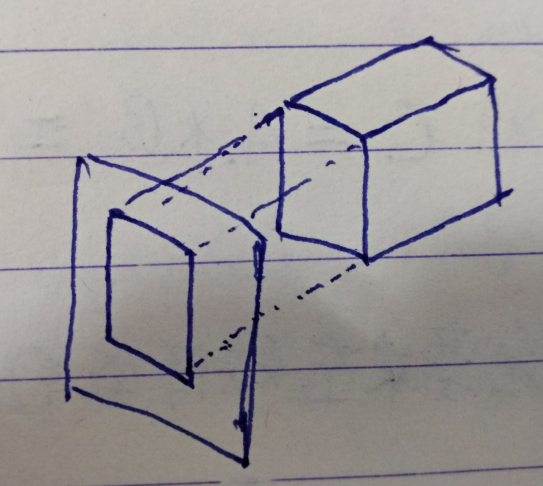
2.透视投影:原理和正交投影相同,但并不保持距离和角度大小的不变.

 

~ 坐标的仿射变换

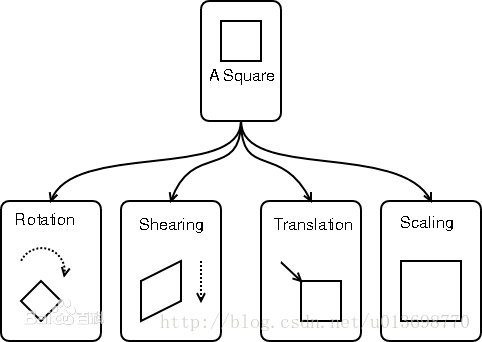
指平面内的平移、旋转、错切和缩放等的变换前后在同一平面上，仿射变换是指平面内的平移、旋转、错切和缩放。这四种变换均可以通过仿射矩阵的实现。如下图所示