1018Big Number用斯特林公式的简化公式和不用公式解决

1018http://acm.hdu.edu.cn/showproblem.php?pid=1018

在其中要体现一下几个问题：

一、一个整数的位数计算

二、优化算法

设有一个整数n，且10^x-1≤n<10^x ,那么我们可以得出其n的位数是x

由于题目中已知1 ≤ n ≤ 10⁷ 所以同时去lg对数则：lg10^x-1≤lg n<lg10^x 得到x-1≤lg n< x所以（int）lg n = x-1

最终得出x = （int）lg n +1；

所以求n阶乘的可以变换成：

（int）lg （1*2*3···*n） +1

在这里可以用下面for代码实现：

sum = 0.0;
for ( j = 1.0; j < num+1; j++)
{
    sum += (log10(j));
}
sum += 1;

其完整代码如下：

#include <stdio.h>
#include <stdlib.h>
#include<math.h>

int main(){
    int n,i,num;
    double sum,j;
    scanf_s("%d", &n);
    for ( i = 0; i < n; i++)
    {
        scanf_s("%d", &num);
        sum = 0.0;
        for ( j = 1.0; j < num+1; j++)
        {
            sum += (log10(j));
        }
        sum += 1;
        printf_s("%d\n", (int)sum);
    }
}

但是在时间复杂度上我们可以看到O（n*（num+1））

Run ID	Submit Time	Judge Status	Pro.ID	Exe.Time	Exe.Memory	Code Len.	Language	Author
9886801	2013-12-24 13:40:57	Accepted	1018	406MS	248K	305 B	C

 

在优化中我们可以使用斯特林公式的简化公式

                                                        

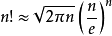
该公式常用来计算与阶乘有关的各种极限。

此为斯特林公式的简化公式。

                                                        

 

故此我们可以将内侧的foe循环代码改进

Run ID	Submit Time	Judge Status	Pro.ID	Exe.Time	Exe.Memory	Code Len.	Language	Author
9886934	2013-12-24 14:23:40	Accepted	1018	15MS	248K	360 B	C

 

#include <stdio.h>
#include <stdlib.h>
#include<math.h>

#define PI  3.1415926535898
#define E   2.71828182845904523536028747135266250

int main(){
    int n,i,num;
    double sum,j;
    scanf_s("%d", &n);
    for ( i = 0; i < n; i++)
    {
        scanf_s("%d", &num);        
        sum = log10(sqrt(2.0 * PI * num)) + num * log10(num / E);
        printf_s("%d\n", (int)sum + 1);
    }
}