机器学习-Kmeans

1|0一、什么是聚类算法？

1、用于发现共同的群体(cluster)，比如：邮件聚类、用户聚类、图片边缘。

2、聚类唯一会使用到的信息是：样本与样本之间的相似度（跟距离负相关）

给定N个训练样本(未标记的){x 1 , . . . , x N },同时给定结果聚类的个数K 目标：把比较“接近”的样本放到一个cluster里，总共得到K个cluster

 

2|0二、不同场景的判定内容

图片检索：图片内容相似度

图片分割：图片像素(颜色)相似度

网页聚类：文本内容相似度

社交网络聚类：(被)关注人群，喜好，喜好内容

电商用户聚类：点击/加车/购买商品，行为序列…

3|0三、样本—向量—距离

 

4|0 四、Kmeans聚类和层次聚类

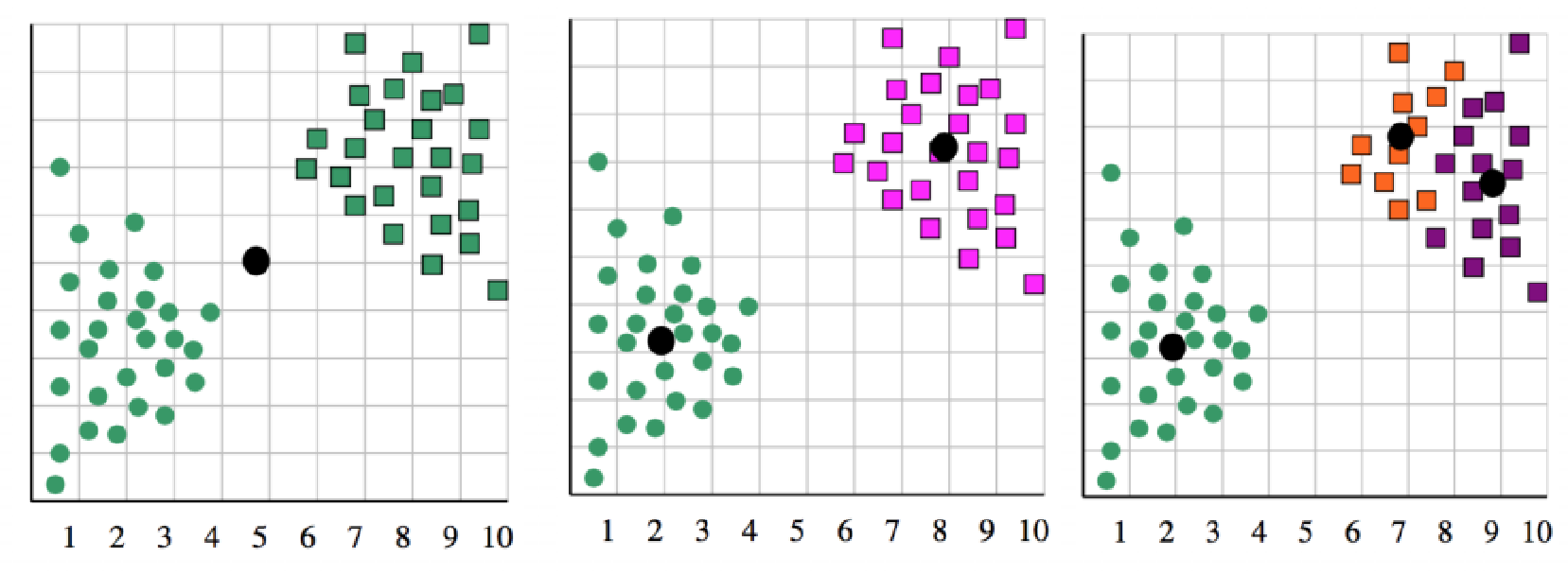
4|1Kmeans聚类：

得到的聚类是一个独立于另外一个的

 

 

 

 

收敛：

聚类中心不再有变化 每个样本到对应聚类中心的距离之和不再有很大变化

 

 

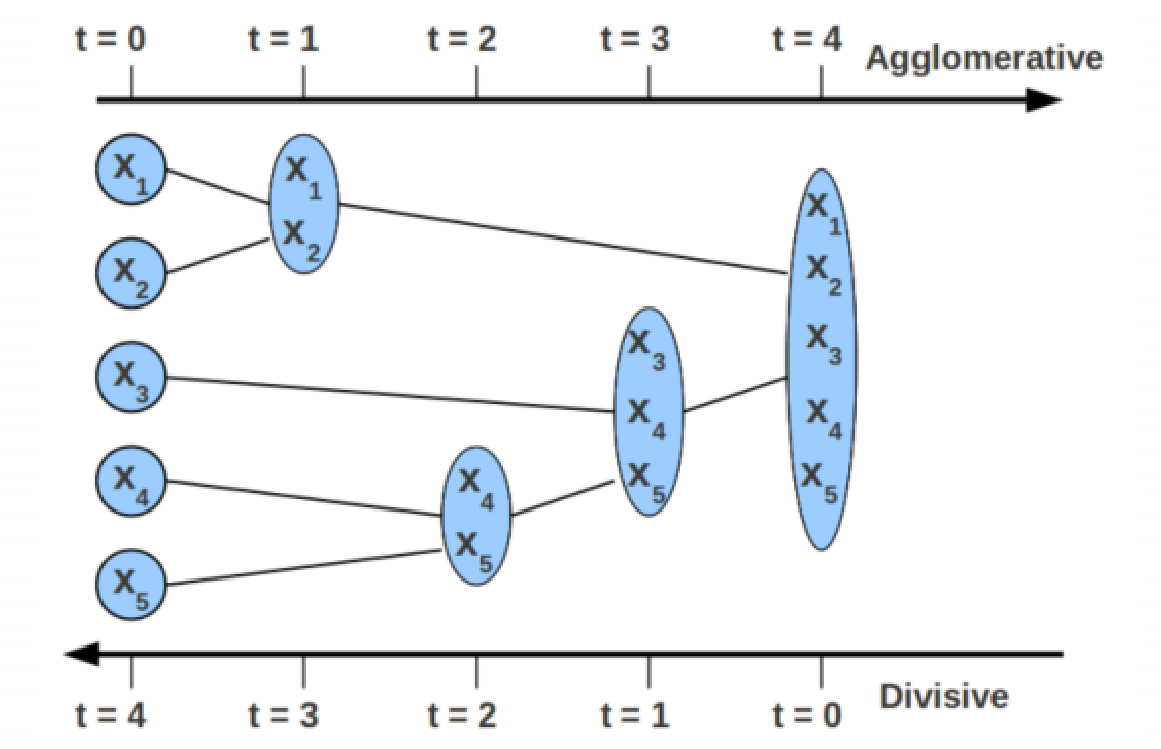
4|2层次聚类：

可以看做树状层叠 无需初始输入聚类个数

 

4|3k-means聚类与层次聚类区别：

kmeans每次聚类产生一个聚类结果，层次聚类可以通过聚类程度不同产生不同结果 kmeans需要指定聚类个数K，层次聚类不用 kmeans比层次聚类更快 kmeans用的多，且可以用k-median

5|0 五、损失函数

 

6|0 六、K的选定

6|1k值的影响：

k过大过小对结果都不好

 

 

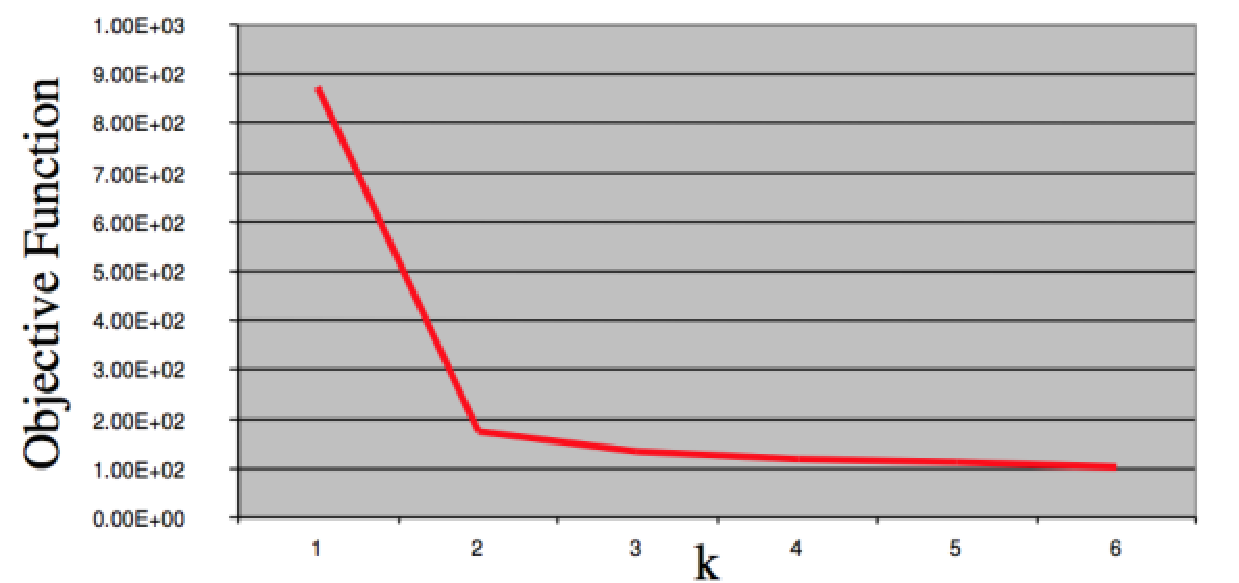
6|2“肘点”法：

选取不同的K值，画出损失函数曲线，选取“肘点”值

 

7|0 七、优缺点

7|1优点：

1. 易于理解，聚类效果不错；

2. 处理大数据集的时候，该算法可以保证较好的伸缩性和高效率；

3. 当簇近似高斯分布的时候，效果非常不错 。

7|2缺点：

1. k值是用户给定的，进行数据处理前，k值是未知的，不同的k值得到的结果不一样；

2. 对初始簇中心点是敏感的；

3. 对于团状的数据点集区分度好，对于带状(环绕)等“非凸”形状不太好。(用谱聚类或者做特征映射)

4. 对异常点的“免疫力”很差，我们可以通过一些调整(比如中心不直接取均值，而是找均值最近的样本点代替)

8|0八、代码示例

import random
import matplotlib.pyplot as plt

class Kmeans():
    def __init__(self,k):
        '''
        初始化
        param k:代表聚类中心个数
        '''
        self.__k=k
        self.__data = [] #存放原始数据
        self.__pointCenter = [] #存放聚类中心点
        self.__result = [] #存放最后的聚类结果
        for i in range(k):
            self.__result.append([])
            
    def calDistance(self,points1,points2):
        '''
        欧氏距离:sprt(x1-x2)^2+(y1-y2)^2
        param points1:一维列表
        param points2:一维列表
        return:两点之间直线距离
        '''
        distance = (sum([(x1-x2)**2 for x1,x2 in zip(points1, points2)]))**0.5 #开平方
        return distance

    def randomCenter(self):
        '''
        生成self.__pointCenter:初次聚类中心点列表
        return:
        '''
        while len(self.__pointCenter)<self.__k:
            index = random.randint(0,len(self.__data)) #得到0到len(self.__data)-1之间的索引
            if self.__data[index] not in self.__pointCenter: #用索引值得到列表的值
                self.__pointCenter.append(self.__data[index])
    
    def calPointToCenterDistance(self,data,center):
        '''
        计算每个店和聚类中心之间的距离
        param data:原始数据
        param center:中心聚类点
        return:距离
        '''
        distance = []
        for i in data:
            distance.append([self.calDistance(i,centerpoint) for centerpoint in center])
        return distance
    
    def sortPoint(self,distance):
        '''
        对原始数据进行分类，将每个点分到离它最近的聚类中心点
        param distance:得到的距离
        return:返回最终的分类结果
        '''
        for i in distance:
            index = i.index(min(i)) #得到五个距离之中的最小值的索引
            self.__result[index].append(self.__data[i]) #通过索引进行分类
        return self.__result
    
    def calNewCenterPoint(self,result):
        '''
        计算新的中心点：通过生成新的聚类求取新的平均值
        param result:分类结果
        return:返回新的聚类中心点
        '''
        newCenterPoint1 = []
        for temp in result:
            #进行转置，将N*M转为M*N形式，将所有point.x值和point,y值撞到一个列表中,便于求取新的平均值
            temps = [[temp[x][i] for x in range(len(temp))] for i in range(len(temp[0]))]
            point = []
            for i in temps:
                point.append(sum(i)/len(i)) #求和再除以数组长度,求取平均值
            newCenterPoint1.append(point)
        return newCenterPoint1
    
    def calCenterToCenterDistance(self,old,new):
        '''
        迭代结束条件
        计算新旧中心点之间的距离
        param old:
        param new:
        return:
        '''
        total = 0
        for point1,point2 in zip(old,new):
            total += self.calDistance(point1,point2)
        return total/len(old)
    
    def fit(self,data,threshold,time=50000):
        self.__data = data
        self.randomCenter()
        print(self.__pointCenter)
        centerDistance = self.calPointToCenterDistance(self.__data,self.__pointCenter)
        
        #对原始数据进行分类，将每个点分到离它最近的中心点
        i = 0
        for temp in centerDistance:
            index = temp.index(min(temp))
            self.__result[index].append(self.__data[i])
            i +=1
        #打印分类结果
        print(self.__result)
        oldCenterPoint = self.__pointCenter
        newCenterPoint = self.calNewCenterPoint(self.__result)
        while self.calCenterToCenterDistance(oldCenterPoint,newCenterPoint) > threshold:
            time -= 1
            result = []
            for i in range(self.__k):
                result.append([])
            #保存上次的中心点
            oldCenterPoint = newCenterPoint
            centerDistance = self.calPointToCenterDistance(self.__data,newCenterPoint)
            #对原始数据进行分类,将每个点分到离它最近的中心点
            i = 0
            for temp in centerDistance:
                index = temp.index(min(temp))
                result[index].append(self.__data[i])
                i += 1
            newCenterPoint = self.calNewCenterPoint(result)
            print(self.calCenterToCenterDistance(oldCenterPoint,newCenterPoint))
            self.__result = result
        self.__pointCenter = newCenterPoint
        return newCenterPoint,self.__result
    
if __name__ == "__main__":
    data = []
    k = 6 #分类数量
    for i in range(len(data)):
        kmeans = Kmeans(k=k)
        centerPoint,result = kmeans.fit(data,0.0001)
        print(centerPoint)
        plt.plot()
        plt.title('Kmeans')
        i = 0
        tempx = []
        tempy = []
        color = []
        for temp in result:
            temps = [[temp[x][i] for x in range(len(temp))] for i in range(len(temp[0]))]
            color += [i]*len(temps[0])
            tempx += temps[0]
            tempy += temps[1]
            i+=2
        plt.scatter(tempx,tempy,c=color,s=30)
        plt.show()

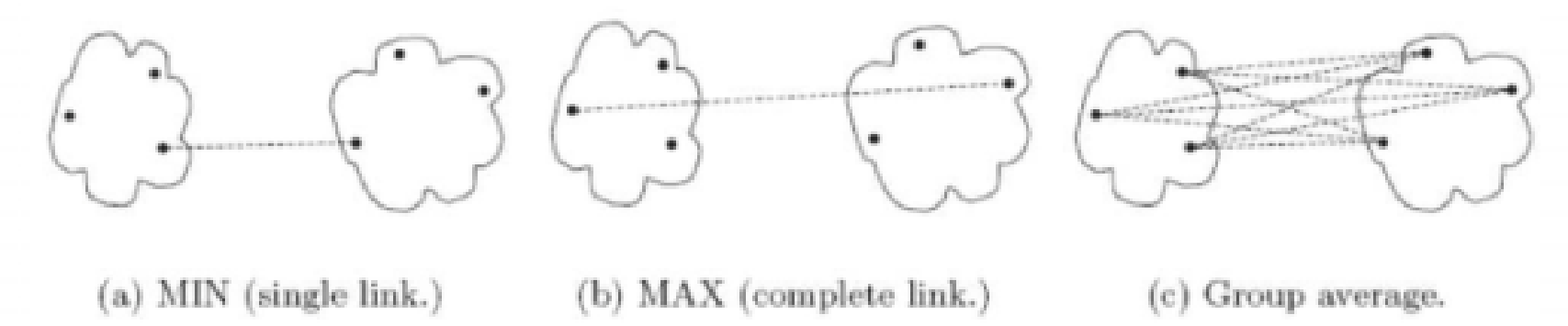
9|0九、层次聚类

 

9|1 cluster R和cluster S之间距离怎么界定？

 

 

 

__EOF__

作　　者：逸繁
出　　处：https://www.cnblogs.com/songyifan427/p/16498805.html
关于博主：编程路上的小学生，热爱技术，喜欢专研。评论和私信会在第一时间回复。或者直接私信我。
版权声明：署名 - 非商业性使用 - 禁止演绎，协议普通文本 | 协议法律文本。
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！