利用逻辑回归进行简单的人群分类解决广告推荐问题

一、什么是逻辑回归？

　　逻辑回归又称对数几率回归是离散选择法模型之一，逻辑回归是一种用于解决监督学习问题的学习算法，进行逻辑回归的目的是使训练数据的标签值与预测出来的值之间的误差最小化。logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。

Logistic回归模型的适用条件：

1. 因变量为二分类的分类变量或某事件的发生率，并且是数值型变量。但是需要注意，重复计数现象指标不适用于Logistic回归。
2. 残差和因变量都要服从二项分布。二项分布对应的是分类变量，所以不是正态分布，进而不是用最小二乘法，而是最大似然法来解决方程估计和检验问题。
3. 自变量和Logistic概率是线性关系
4. 各观测对象间相互独立

 

原理：

　　如果直接将线性回归的模型扣到Logistic回归中，会造成方程二边取值区间不同和普遍的非直线关系。因为Logistic中因变量为二分类变量，某个概率作为方程的因变量估计值取值范围为0-1，但是，方程右边取值范围是无穷大或者无穷小。所以，才引入Logistic回归。

 

Logistic回归实质：

　　发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。

 

二、Logistic函数/sigmoid函数的原理与实现

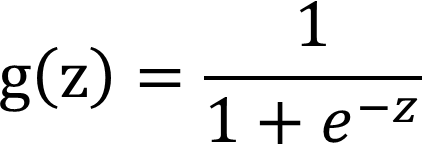
实现：

import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-6,6,1000)
y=[1/(1+np.exp(-i)) for i in x]
plt.plot(x,y)
plt.grid(True)

 

 

 

 

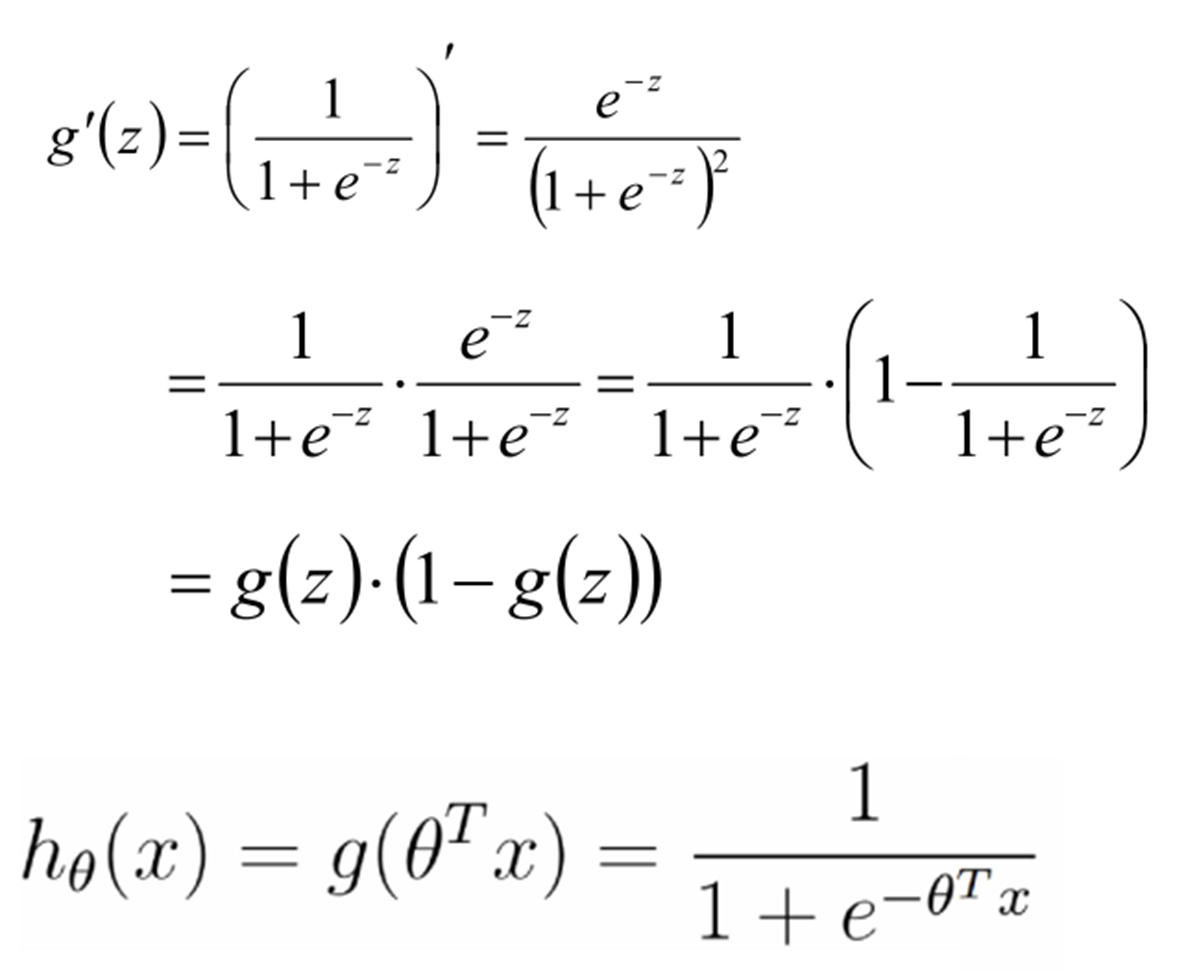
最大似然估计

 

 

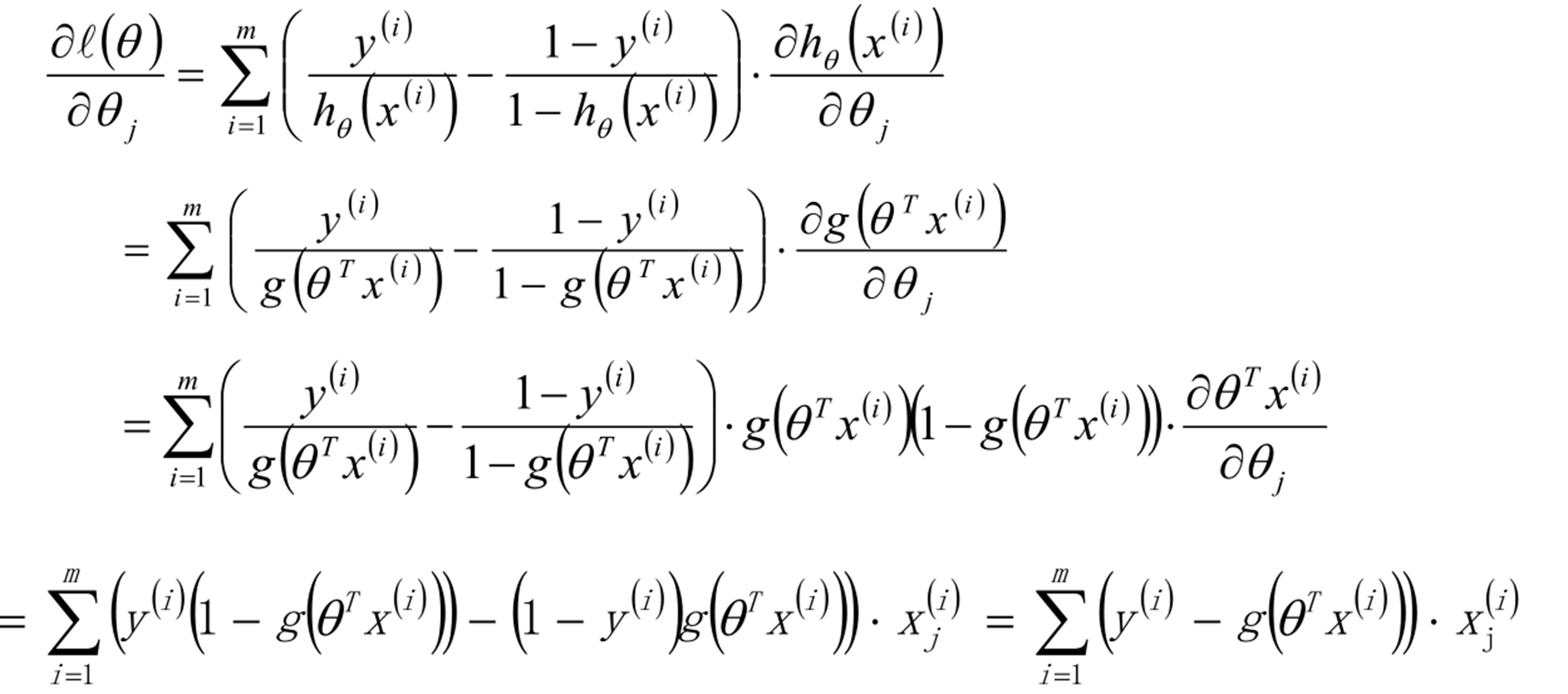
结论：

 

假设

 

 

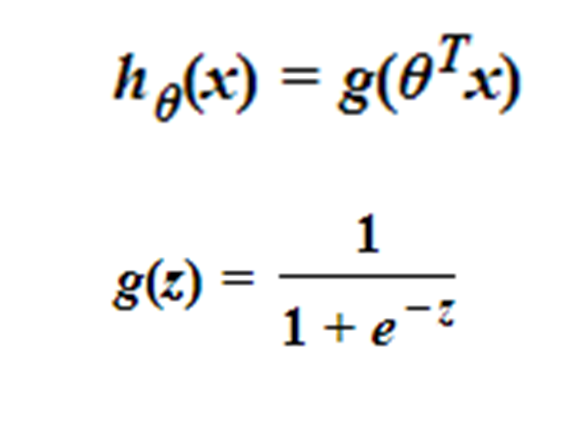
损失函数

梯度

 

三、为了进行广告推荐对目标人群简单分类

1.逻辑回归步骤

1. 收集数据
2. 读取数据，处理数据，查看各数据的缺失情况（如果缺失需要借助于删除法、替换法、插值法等 完成缺失值的处理）对定性变量数值化，剔除无关变量，构建常数项
3. 分析数据，将数据分为训练集和测试集，交叉验证，构建逻辑回归分类器，调整优化，得出参数值
4. 测试算法，完成预测

2.以一组可能买房的用户信息数据为例

（User ID：用户id Gender：性别 Age：年龄 EstimatedSalary：收入 Purchased：是否已经购买）

3.代码示例：

 

 

import pandas as pd
import matplotlib.pyplot as plt
purchase=pd.read_csv("logistic_data.csv")
purchase.head()
dummy = pd.get_dummies(purchase.Gender)
dummy.head()
# 为防止多重共线性，将哑变量中的Female删除
dummy_drop = dummy.drop('Female', axis = 1)#把female列删除
dummy_drop.head()
purchase = purchase.drop(['User ID','Gender'], axis = 1)
model_data = pd.concat([dummy_drop,purchase], axis = 1)
X = model_data.drop('Purchased', axis = 1)
y = model_data['Purchased']
X.head()
model_data['Purchased'].value_counts()

from sklearn import linear_model
clf=linear_model.LogisticRegression()
clf.fit(X,y)
clf.coef_
clf.score(X,y)

 

 

四、逻辑回归优缺点

1.优点

• 形式简单，模型的可解释性强。 从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。
• 训练速度较快。
• 资源占用内存小。只需要存储各个维度的特征值。
• 模型效果不错。在工程上可以接受（作为baseline），如果特征工程好，效果不会太差，并且特征工程可以大家并行开发，大大加快开发速度。
• 输出所属类别概率。可以很方便的得到最后的分类结果。

2.缺点：

• 准确率不是很高。形式简单，很难去拟合数据的真实分布。
• 很难处理数据不平衡的问题。eg.比如正负样本比是10000:1，把所有样本都预测为正也能使损失函数的值比较小，但是作为一个分类器，它对正负样本的区分能力不会很好。
• 本身无法筛选特征。用GBDT筛选特征，结合逻辑回归