概率论笔记（五）随机向量/多元随机变量

文章目录

• 一：联合分布
• • 1.1联合分布函数
  • 1.2二维离散型随机向量及其联合分布列
  • 1.3二维连续型随机向量及其联合密度函数
• 二：边缘分布与随机变量的独立性
• • 2.1边缘分布
  • 2.2随机变量的独立性
  • 2.3两个随机变量下的函数的分布
  • • 2.3.1离散型
    • 2.3.2连续型

---

一：联合分布

引入：

---

1.1联合分布函数

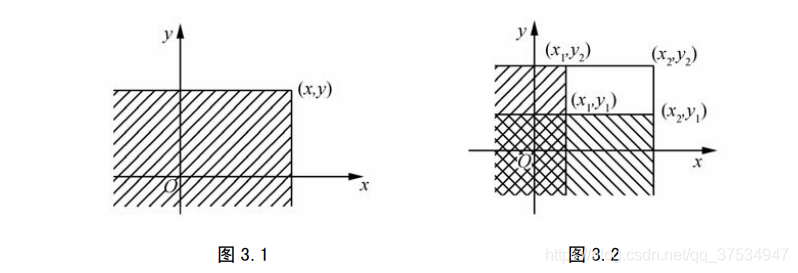
注：相比于一维的分布函数，其增加了一维空间，成了二维空间，测试整体的二维空间变成了整体的1；之后同样是概率的累计。

---

1.2二维离散型随机向量及其联合分布列

---

1.3二维连续型随机向量及其联合密度函数

性质：

---

二：边缘分布与随机变量的独立性

2.1边缘分布

联合分布函数求边缘分布函数：

注：其意义就是在不管其中一个变量（不局限其范围，即最大范围）的时候，求另一个变量。其中例子见参考书吧。

---

2.2随机变量的独立性

注： 见上面的最后一段，需要注意的是，之前咱们可以从联合分布求边缘分布，而从边缘分布求联合分布一般是不可能的，但是当X和Y独立的时候，边缘分布求联合分布是可以的。

---

2.3两个随机变量下的函数的分布

注：其类似于复合随机，见：https://blog.csdn.net/qq_37534947/article/details/109587828，只是增加成了两个变量。

2.3.1离散型

2.3.2连续型

---

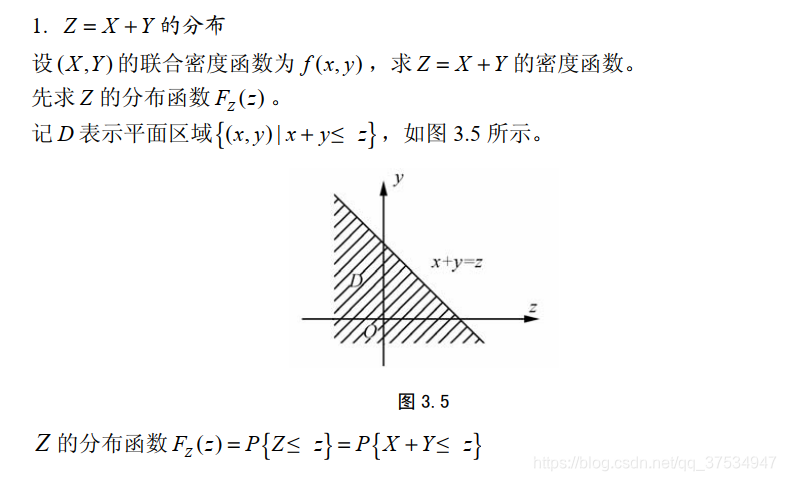
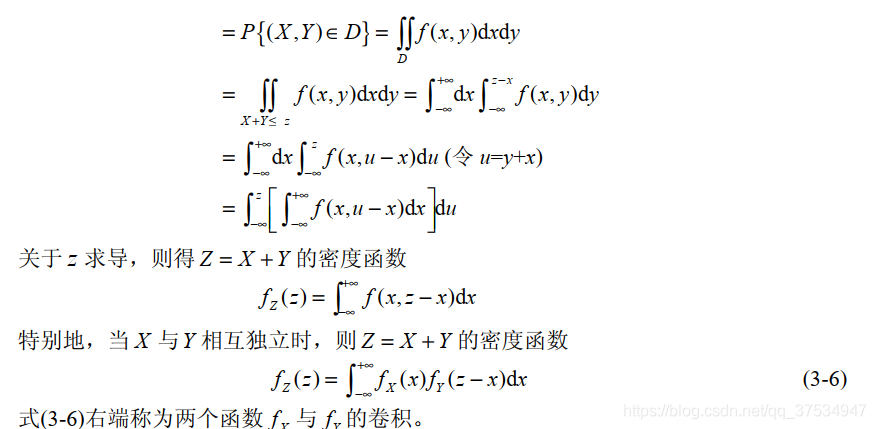
参考书籍：
概率论与数理统计 黄清龙.pdf