BZOJ 3083 遥远的国度(树链剖分)

3083: 遥远的国度

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 5003  Solved: 1434
[Submit][Status][Discuss]

Description

描述
zcwwzdjn在追杀十分sb的zhx，而zhx逃入了一个遥远的国度。当zcwwzdjn准备进入遥远的国度继续追杀时，守护神RapiD阻拦了zcwwzdjn的去路，他需要zcwwzdjn完成任务后才能进入遥远的国度继续追杀。

问题是这样的：遥远的国度有n个城市，这些城市之间由一些路连接且这些城市构成了一颗树。这个国度有一个首都，我们可以把这个首都看做整棵树的根，但遥远的国度比较奇怪，首都是随时有可能变为另外一个城市的。遥远的国度的每个城市有一个防御值，有些时候RapiD会使得某两个城市之间的路径上的所有城市的防御值都变为某个值。RapiD想知道在某个时候，如果把首都看做整棵树的根的话，那么以某个城市为根的子树的所有城市的防御值最小是多少。由于RapiD无法解决这个问题，所以他拦住了zcwwzdjn希望他能帮忙。但zcwwzdjn还要追杀sb的zhx，所以这个重大的问题就被转交到了你的手上。

 

 

Input

第1行两个整数n m，代表城市个数和操作数。
第2行至第n行，每行两个整数 u v，代表城市u和城市v之间有一条路。
第n+1行，有n个整数，代表所有点的初始防御值。
第n+2行一个整数 id，代表初始的首都为id。
第n+3行至第n+m+2行，首先有一个整数opt，如果opt=1，接下来有一个整数id，代表把首都修改为id；如果opt=2，接下来有三个整数p1 p2 v，代表将p1 p2路径上的所有城市的防御值修改为v；如果opt=3，接下来有一个整数 id，代表询问以城市id为根的子树中的最小防御值。

Output

对于每个opt=3的操作，输出一行代表对应子树的最小点权值。

Sample Input

3 7
1 2
1 3
1 2 3
1
3 1
2 1 1 6
3 1
2 2 2 5
3 1
2 3 3 4
3 1

Sample Output

1
2
3
4
提示
对于20%的数据，n<=1000 m<=1000。
对于另外10%的数据，n<=100000，m<=100000，保证修改为单点修改。
对于另外10%的数据，n<=100000，m<=100000，保证树为一条链。
对于另外10%的数据，n<=100000，m<=100000，没有修改首都的操作。
对于100%的数据，n<=100000，m<=100000，0<所有权值<=2^31。

HINT

 

Source

zhonghaoxi提供

题解：

这题有换根操作，但按照普通的思路我们可以发现，换根之后树的形态会有改变，每个节点的子树会发生改变，所以我们来分类讨论。

修改链的操作不会发生改变，现在只考虑子树minn。为了方便，我们定义现在的换的“根节点”为root（但实际上树的根节点为1），子树根为x，黑圈标明查询范围；

情况一   x=root，很显然此时应当查询整棵树。

 

 

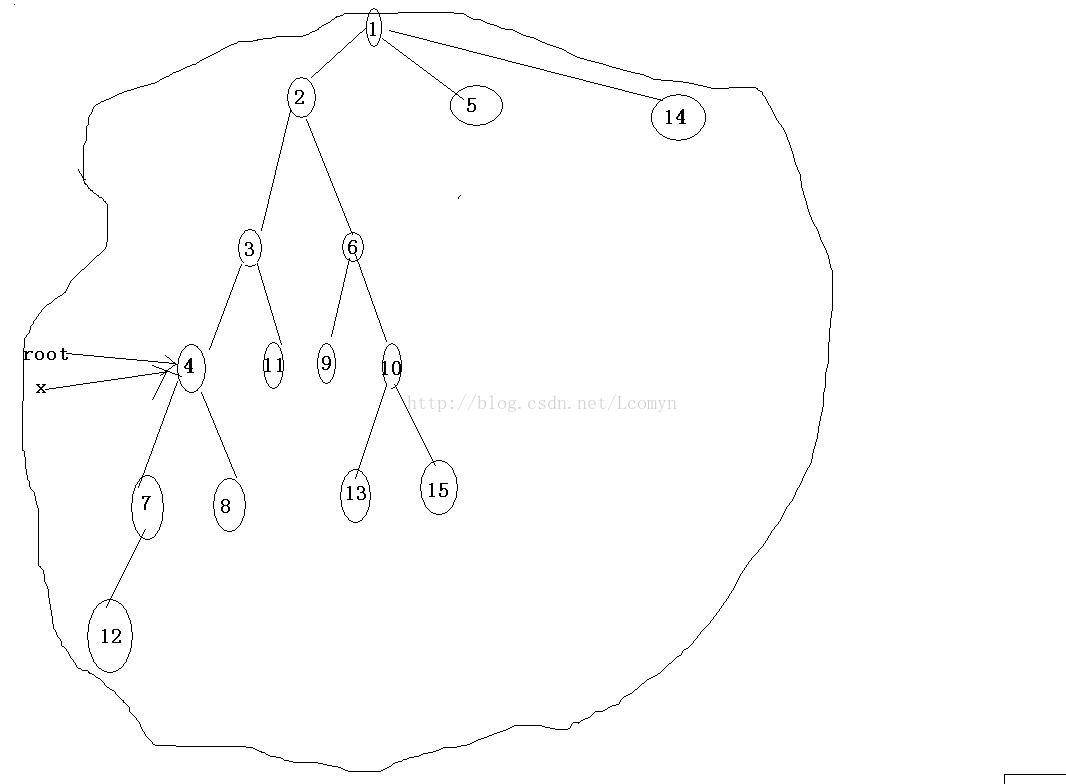
情况二 lca(root,x)!=x ,此时直接查询x的子树即可，与换根无关。

 

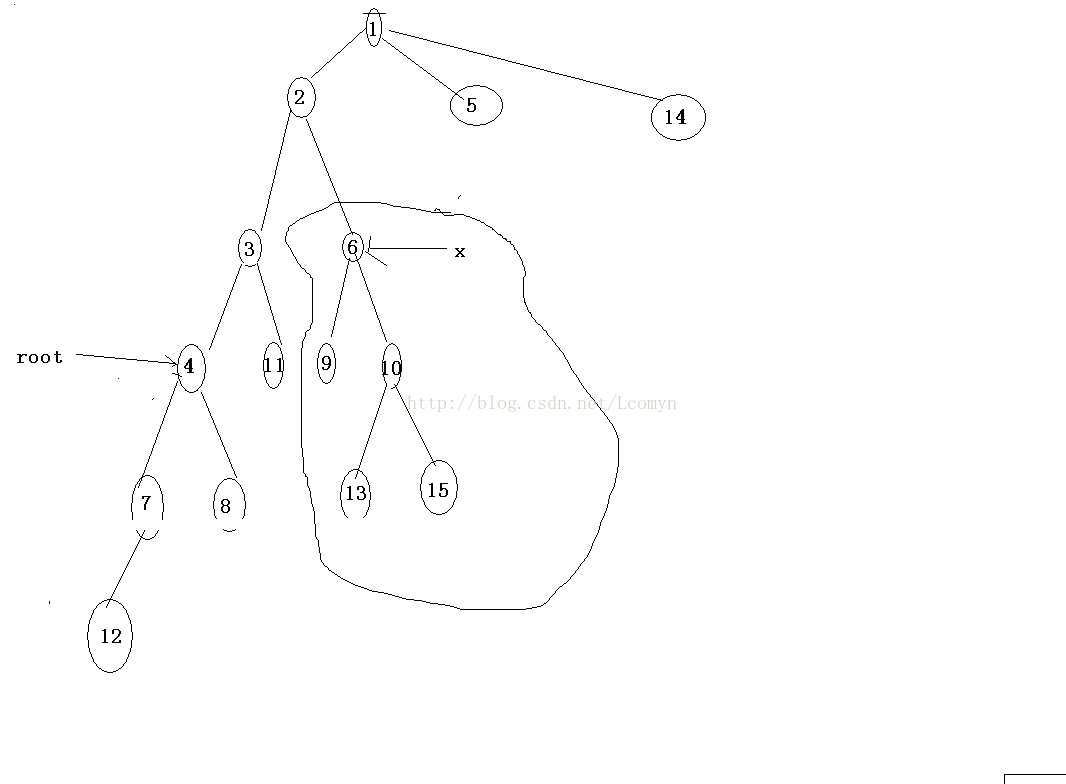
情况三，lca(root,x)=x，此时我们应当查询与x相邻的节点中与root最近的点v在整棵树中的补集

 

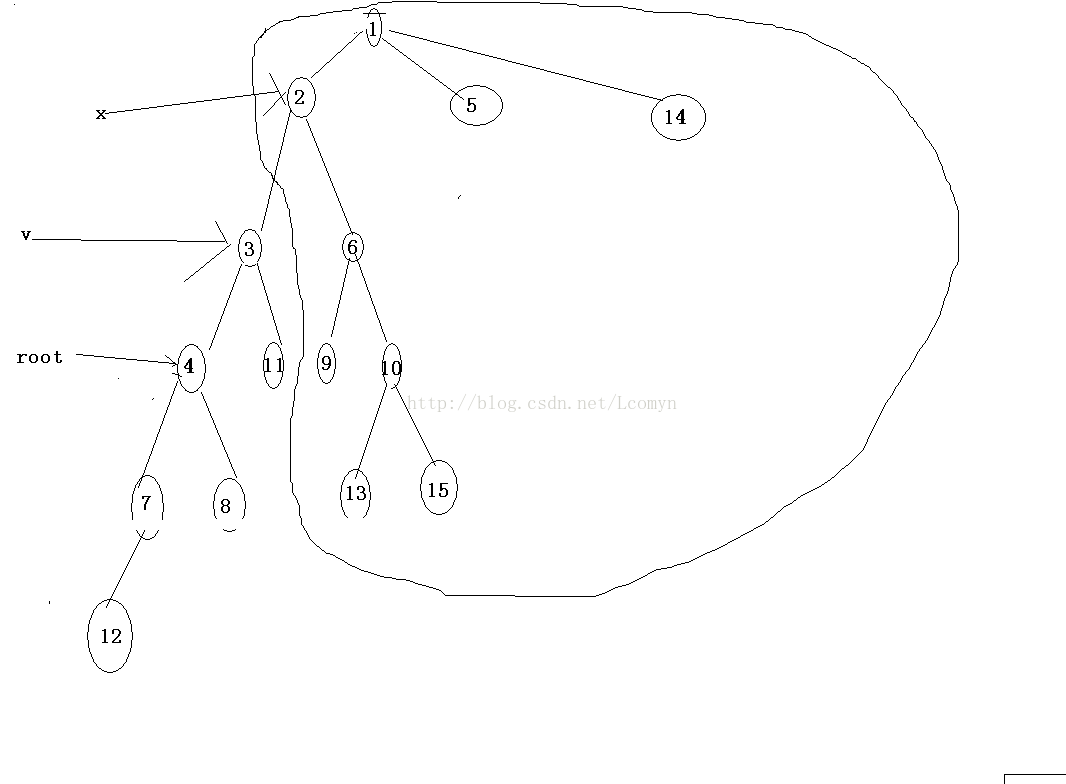
可以发现v一定在root到x的链上，且一定是x在这条链上的儿子，倍增法可以求得v

BZOJ TLE也返回RE？？?  用普通树剖一直RE，用倍增就过了Orz.

参考代码：

#include<bits/stdc++.h>
using namespace std;
#define clr(a,b) memset(a,b,sizeof (a))
#define PI acos(-1.0)
typedef long long ll;
const int maxn=2e5+10;
const int INF=0x3f3f3f3f;
/*首先有一个整数opt如果opt=1接下来有一个整数id代表把首都修改
为id如果opt=2接下来有三个整数p1 p2 v代表将p1 p2路径上的所有
城市的防御值修改为v如果opt=3接下来有一个整数 id代表询问以城
市id为根的子树中的最小防御值*/
int n,m,op,xx,yy,zz,a[maxn],head[maxn];
int siz[maxn],son[maxn],fa[maxn],top[maxn],deep[maxn];
int tid[maxn],rnk[maxn],f[maxn][20],cnt,tot;
struct Edge{
    int v,nxt;
} edge[maxn<<1];
void addedge(int x,int y) 
{
    edge[tot].v=y;
    edge[tot].nxt=head[x];
    head[x]=tot++;
}

inline void dfs1(int x)
{
    siz[x]=1; 
    for(int i=1;i<=19;++i) { if((1<<i)<=deep[x]) f[x][i]=f[f[x][i-1]][i-1];else break;  }
    for(int i=head[x];~i;i=edge[i].nxt)
    {
        int v=edge[i].v;
        if(v!=fa[x]) 
        {
            fa[v]=f[v][0]=x;
            deep[v]=deep[x]+1;
            dfs1(v);
            siz[x]+=siz[v];
            if(son[x]==-1||siz[son[x]]<siz[v]) son[x]=v; 
        }
    }
}

inline void dfs2(int x,int tp)
{
    tid[x]=++cnt;rnk[cnt]=x;top[x]=tp;
    if(son[x]==-1) return;
    dfs2(son[x],tp);
    for(int i=head[x];~i;i=edge[i].nxt)
    {
        int v=edge[i].v;
        if(v!=fa[x]&&v!=son[x]) dfs2(v,v);
    }

}

struct Tree{
    int l,r,min_num;
    int tag;
} tree[maxn<<4];

inline void pushup(int rt)
{
    tree[rt].min_num=min(tree[rt<<1].min_num,tree[rt<<1|1].min_num);
}
inline void pushdown(int rt)
{
    tree[rt<<1].tag=tree[rt<<1|1].tag=tree[rt].tag;
    tree[rt<<1].min_num=tree[rt<<1|1].min_num=tree[rt].tag;
    tree[rt].tag=-1;
}

inline void Build(int rt,int l,int r)
{
    tree[rt].l=l,tree[rt].r=r;tree[rt].tag=-1;
    if(l==r){ tree[rt].min_num=a[rnk[l]]; return ;}
    int mid=l+r>>1;
    Build(rt<<1,l,mid);Build(rt<<1|1,mid+1,r);
    pushup(rt);
}

inline void Insert(int rt,int L,int R,int val)//1
{
    if(tree[rt].l>=L&&tree[rt].r<=R){tree[rt].min_num=tree[rt].tag=val;return;}
    if(~tree[rt].tag) pushdown(rt);
    int mid=(tree[rt].l+tree[rt].r)>>1;
    if(R<=mid) Insert(rt<<1,L,R,val);
    else if(L>=mid+1) Insert(rt<<1|1,L,R,val); 
    else Insert(rt<<1,L,mid,val),Insert(rt<<1|1,mid+1,R,val);
    pushup(rt);
}
//1和2用倍增来把x~y的值变为val 
inline void Update(int x,int y,int val)//2
{
    int fx=top[x],fy=top[y];
    while(fx!=fy)
    {
        if(deep[fx]<deep[fy]) swap(x,y),swap(fx,fy);
        Insert(1,tid[fx],tid[x],val);
        x=fa[fx],fx=top[x];
    }
    if(deep[x]>deep[y]) swap(x,y);
    Insert(1,tid[x],tid[y],val);
}

inline int Query(int rt,int L,int R)
{
    if(tree[rt].l>=L&&tree[rt].r<=R) return tree[rt].min_num;
    if(~tree[rt].tag) pushdown(rt);
    int mid=tree[rt].l+tree[rt].r>>1;
    if(R<=mid) return Query(rt<<1,L,R);
    else if(L>=mid+1) return Query(rt<<1|1,L,R);
    else return min(Query(rt<<1,L,mid),Query(rt<<1|1,mid+1,R));    
} 

inline int LCA(int x,int y)
{
    int fx=top[x],fy=top[y];
    while(fx!=fy)
    {
        if(deep[fx]<deep[fy]) swap(x,y),swap(fx,fy);
        x=fa[fx],fx=top[x];
    }
    return deep[x]>deep[y] ? y:x;
}

inline void Init()
{
    clr(head,-1);clr(son,-1);
    clr(f,0);cnt=0;tot=1;
}
int main()
{
    Init();int root;deep[1]=1;
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;++i) scanf("%d%d",&xx,&yy),addedge(xx,yy),addedge(yy,xx);
    for(int i=1;i<=n;++i) scanf("%d",&a[i]);
    dfs1(1),dfs2(1,1);Build(1,1,n);
    scanf("%d",&root);
    while(m--)
    {
        scanf("%d%d",&op,&xx);
        if(op==1) root=xx;
        else if(op==2) { scanf("%d%d",&yy,&zz),Update(xx,yy,zz); }
        else
        {
            if(root==xx) { printf("%d\n",tree[1].min_num);continue;}
            int lca=LCA(xx,root);
            if(xx!=lca) printf("%d\n",Query(1,tid[xx],tid[xx]+siz[xx]-1));
            else
            {
                int tmp=deep[root]-deep[xx]-1,ans=INF;yy=root;
                for(int i=0;i<=19;++i) if((1<<i)&tmp) yy=f[yy][i];
                if(tid[yy]>1) ans=Query(1,1,tid[yy]-1);
                if(tid[yy]+siz[yy]<=n) ans=min(ans,Query(1,tid[yy]+siz[yy],n));
                printf("%d\n",ans);
            }
        }
    }
    return 0;
}
/*
3 7
1 2
1 3
1 2 3
1
3 1
2 1 1 6
3 1
2 2 2 5
3 1
2 3 3 4
3 1
*/