BZOJ 3033 太鼓达人（DFS+欧拉回路）

Description

　　七夕祭上，Vani牵着cl的手，在明亮的灯光和欢乐的气氛中愉快地穿行。这时，在前面忽然出现了一台太鼓达人机台，而在机台前坐着的是刚刚被精英队伍成员XLk、Poet_shy和lydrainbowcat拯救出来的的applepi。看到两人对太鼓达人产生了兴趣，applepi果断闪人，于是cl拿起鼓棒准备挑战。然而即使是在普通难度下，cl的路人本性也充分地暴露了出来。一曲终了，不但没有过关，就连鼓都不灵了。Vani十分过意不去，决定帮助工作人员修鼓。

　　鼓的主要元件是M个围成一圈的传感器。每个传感器都有开和关两种工作状态，分别用1和0表示。显然，从不同的位置出发沿顺时针方向连续检查K个传感器可以得到M个长度为K的01串。Vani知道这M个01串应该是互不相同的。而且鼓的设计很精密，M会取到可能的最大值。现在Vani已经了解到了K的值，他希望你求出M的值，并给出字典序最小的传感器排布方案。

Input

　　一个整数K。

　

Output

　一个整数M和一个二进制串，由一个空格分隔。表示可能的最大的M，以及字典序最小的排布方案，字符0表示关，1表示开。你输出的串的第一个字和最后一个字是相邻的。

Sample Input

3

Sample Output

8 00010111

HINT

　得到的8个01串分别是000、001、010、101、011、111、110和100。注意前后是相邻的。长度为3的二进制串总共只有8种，所以M = 8一定是可能的最大值。


　　对于全部测试点，2≤K≤11。

题解：题目大意：给出k，求一个最长的M位01串，使其从每一个位置向后走k个得到的M个k位01串互不相同（最后一个和第一个相邻，即是一个环）。输出字典序最小的答案

这道题实际上是将k-1位的二进制数看做点，k位的二进制数看成边，并且连接两个点的边就是将这两个点的权怼起来 
像这样 

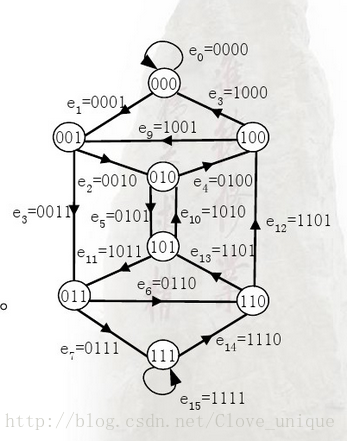
然后每个点的入度和出度相等并且全部是偶点，是一个标准的欧拉图，所以只需要在这个图中找字典序最小的欧拉回路就行了。暴力搜索欧拉回路就行了

参考代码为：

 1 /**************************************************************
 2     Problem: 3033
 3     User: SongHL
 4     Language: C++
 5     Result: Accepted
 6     Time:64 ms
 7     Memory:1336 kb
 8 ****************************************************************/
 9  
10 #include<bits/stdc++.h>
11 using namespace std;
12 #define mem(a,b) memset(a,b,sizeof a)
13 #define mp make_pair
14 #define eps 1e-8
15 #define lson l,mid,rt<<1
16 #define rson mid+1,r,rt<<1|1
17 typedef long long LL;
18 typedef unsigned long long ull;
19 const int INF=0x3f3f3f3f;
20 const LL inf=0x3f3f3f3f3f3f3f3fll;
21 inline void read(int &k)
22 {
23     int x=0,f=1; char ch=getchar();
24     while(ch<'0'||ch>'9') {if(ch=='-') f=-1; ch=getchar();}
25     while(ch>='0'&&ch<='9') {x=x*10+ch-'0'; ch=getchar(); }
26     k=x*f;
27 }
28 int n,m,msk;
29 int to[2500],vis[2500],ans[2500];
30 int dfs(int x,int y)
31 {
32     if(vis[x])  return 0;
33     vis[x]=1,ans[y]=x&1;
34     if(y==n)    return 1;
35     if(dfs(((x<<1))&msk,y+1)) return 1;
36     if(dfs(((x<<1)|1)&msk,y+1))   return 1;
37     vis[x]=0;
38     return 0;
39 }
40 int main()
41 {
42     scanf("%d",&m);
43     n=1<<m,msk=n-1;
44     printf("%d ",n);
45     dfs(n-2,1);
46     for(int i=1;i<=n;i++) printf("%d",ans[i]);
47     return 0;
48 }
View Code

 

　　

 

posted @ 2018-10-11 01:01  StarHai  阅读(395)  评论(1)  编辑  收藏  举报