循环结构课后反思

课本上总共有7个题目，我记得课上老师说7个题目的难度是逐级递增的，由于看到这么多形形色色的图案感觉到恐惧，于是我便从第一个开始做起，分析以后，发现第一个确实没有想象中那么难，我先看了已经发出来的同学的博客，很少人做了第一个作业，而我发现其实做这一类的题目就是要从简单的开始分析，找到其中的规律，那么难的也能迎刃而解。

第一个图形分析如下：

这是一个标准的菱形，我的想法是把它划分为两个部分，上部分和下部分两个等腰三角形  、 。

上部分的三角形是由五行九列组成，事实上，它是由两个空白的直角三角形和一个星星等腰三角形组成，空白三角形的规律是：第一行4个空格，第二行3个，第三行2个······以此类推，我用 j 来表示空格，i来表示行数，k来表示“ * ”，那么k与i的关系是：总有每一行的 k=2*i -1，而我们可以发现，i最大为5，当i=1，j=4; i=2,j=3;  i=3,j=2,所以推出 j=5-i,那么根据我们推出的结果，使用for语句，注意符号书写问题，以及注意每一行执行完以后需要换行，就可以运行出上半部分的三角形，这是上半部分的三角形的代码：

#include<stdio.h>
main()
{
    int i,j,k;
    for (i=1;i<=5;i++)   //表示行数
    {
        for (j=1;j<=5-i;j++)  //j表示空格
        printf(" ");
        for (k=1;k<=2*i-1;k++)  //k表示*
        printf("*");
        printf("\n");  //记得每打完一行都得换行
        
    }
    
}

下半部分的三角形是由一个倒着的等腰三角形构成，它有四行七列，跟上面的分析一样，我可以把它看成是两个空白直角三角形和一个倒等腰三角形组成，我仍然用i表示行数， j 来表示空格，k来表示“ * ”，当i=1，j=1; i=2;j=2······,推出i=j,而我在想i和k之间的关系的时候，花了一些时间，当i=1,k=7; i=2,k=5; i=3,k=3····我想了想，发现了规律：k=9-2*i,于是根据推出的结果，我写了如下代码：

#include<stdio.h>
main()
{
    int i,j,k;
    for (i=1;i<=5;i++)
    {
        for (j=1;j<=5-i;j++)
        printf(" ");
        for (k=1;k<=2*i-1;k++)
        printf("*");
        printf("\n");
        
    }
    for (i=1;i<=4;i++) //表示行数
    {
        for (j=1;j<=i;j++) //表示空格
        printf(" ");
        for (j=1;j<=9-2*i;j++)  //表示*
        printf("*");  //少了换行！！！
    
    }
}

这是运行效果：（发现原来忘记换行就是这副摸样）

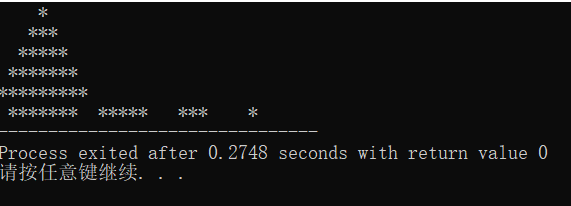
改正以后，运行成功了：（很开心！！！！虽然是第一个，但是也花了不少时间研究了下呢）

 

 

 

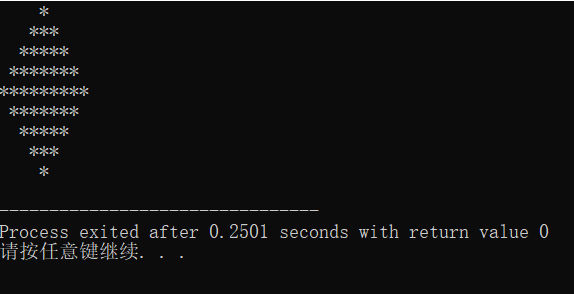
看完并分析运行完第一个图形以后，我发现后面的图形都大同小异，都是按照我刚刚第一个图形的分分析方法进行的，最后我选择了大家都分析了的最后一个图形进行我的分析，

第七个图形分析如下：

这是第7个图形，按照我第一个图形所述的方法，我们可以把它进行拆分，拆成一个等腰三角形、一个矩形、一个矩形挖去一个空白等腰三角形的模样：、、

上部分的等腰三角形是由五行九列组成的，它是由两个空白的直角三角形和一个星星等腰三角形组成，空白三角形的规律是：第一行4个空格，第二行3个，第三行2个······以此类推，我用 j 来表示空格，i来表示行数，k来表示“ * ”，那么k与i的关系是：总有每一行的 k=2*i -1，i最大为5，当i=1，j=4; i=2,j=3;  i=3,j=2,所以推出 j=5-i,我们可以发现，这个图形的上部分与我上面分析的第一个图形的上部分的分析是一样的，并且代码也是一样的，这是它的代码：

#include<stdio.h>
main()
{
    int i,j,k;
    for (i=1;i<=5;i++)    
        {   
        for(j=1;j<=(5-i);j++)    
            {
                printf("     ");
            }
        for(k=1;k<=(2*i-1);k++)
            {
                printf("  *  ");
            }   
        printf("\n");   
        }
}

中间的矩形就比较简单啦，是我们第一节课所学的内容，它是一个两行九列组成的矩形，我们把i表示行，j表示列，写出代码：

 for (i=1;i<=2;i++) 
        {
            for(j=1;j<=9;j++)
            {
                printf("  *  ");
            }
            printf("\n");
        }

下部分可以看成一个矩形挖去一个等腰三角形，而且我们还可以发现，空白的等腰三角形和上部分的等腰三角形是一样的，我们只用把“ * ”换成“  ”即可，而且我们还可以发现，

、，下半部分和第一个图形的上半部分的分析也是一样的，只是把“ ”换成了“ * ”而已，，所以我们可以直接用第一个图形的代码，直接把“ ”换成“ * ”就可以了，代码如下：

for (i=1;i<=4;i++)   
        {   
        for(j=1; j<=(5-i);j++)  //这是下部分左边的三角形
            {
                printf("  *  "); 
            }
        for(k=1;k<=(2*i-1);k++)  //这是下部分中间的空白三角形
            {
                printf("     ");
            }   
        for(j=1;j<=(5-i);j++)  //这是下部分右边的三角形 
            {
                printf("  *  ");
            }
        
        printf("\n");   
        }

把三个部分的代码整合在一起：

#include<stdio.h>
main()
{
    int i,j,k;
    for (i=1;i<=5;i++)    //上部分图形
        {   
        for(j=1;j<=(5-i);j++)    
            {
                printf("     ")；
            }
        for(k=1;k<=(2*i-1);k++)
            {
                printf("  *  "); 
            }   
        printf("\n");   
        }
        
    for (i=1;i<=2;i++)  //中间矩形
        {
            for(j=1;j<=9;j++)
            {
                printf("  *  ");
            }
            printf("\n");
        }
        
    for (i=1;i<=4;i++)  //下部分图形
        {   
        for(j=1; j<=(5-i);j++)  
            {
                printf("  *  "); 
            }
        for(k=1;k<=(2*i-1);k++)
            {
                printf("     ");
            }   
        for(j=1;j<=(5-i);j++) 
            {
                printf("  *  ");
            }
        
        printf("\n");   
        }
 } 

运行成功：

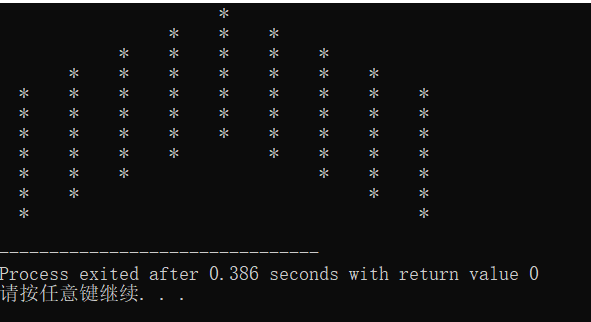
心得感想：我发现图形不管怎么变，都是万变不离其中，每一个复杂的图形都是由简单的等腰三角形或者矩形填充上“ * ”或者“ ”而组成的，我们关键就是要用不同的字母表示他们，并且分析他们之间的数量关系，遇上难的图形，我们就用分割法把他们分开，以后，就发现一个个拆开的图形是我们熟悉的图形，有必要的时候在纸上列出他们分别的数量，寻找出规律，列出数学等式，就可以解决问题。具体的分析方法，我在第一个图形当中有详细的说明。