机器学习(Machine Learning)- 吴恩达(Andrew Ng) 学习笔记(九)
Neural Networks: Learning
在给定训练集的情况下,为神经网络拟合参数的学习方法。
Cost function
Neural Network (Classification) 神经网络在分类问题中的应用
符号说明:
- \(L\) = total no. of layers in network 神经网络中的层数
- \(s_l\) = no. of units (not counting bias unit) in layer \(l\) 第\(l\)层的单元个数(偏置单元不计入内)
下图中的\(L = 4\), \(s_1 = 3\), \(s_2 = 5\), \(s_3 = 5\), \(s_4 = 4\).
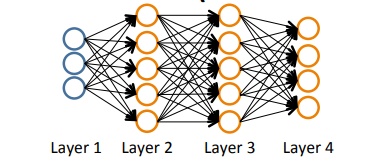
Binary classification:
\(y = 0 or 1\) , 1 output unit. \(s_l = 1\).
Multi-class classification:
\(y \in R^K\), E.g. \(\left[ \begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix} \right]\),\(\left[ \begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix} \right]\),\(\left[ \begin{matrix} 0 \\ 0 \\ 1 \\ 0 \end{matrix} \right]\),\(\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix} \right]\), \(K\) output units. \(s_l = K\).
综上:当只有两个类别时不需要使用一对多方法,\(K \geq 3\)时才会用。
Cost function
神经网络中的代价函数是逻辑回归里使用的代价函数的一般化形式。
Logistic regression:
\(J(\Theta) = -\frac{1}{m}\left[ \sum_{i=1}^my^{(i)}log h_\Theta(x^{(i)}) + (1-y^{(i)})log(1-h_\Theta(x^{(i)})) \right] + \frac{\lambda}{2m}\sum_{j=1}^n\Theta_j^2\)
Neural network:
\(h_\Theta(x) \in R^K\), \((h_\Theta(x))_i = i^{th}\) output
\(J(\Theta) = -\frac{1}{m}\left[ \sum_{i=1}^m\sum_{k=1}^Ky_k^{(i)}log( h_\Theta(x^{(i)}))_k + (1-y_k^{(i)})log(1-(h_\Theta(x^{(i)}))_k) \right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}(\Theta_{ji}^l)^2\)
其中\(m\)是特征值数目的个数,\(K\)是输出单元的数目个数,\(s_l\) 是第\(l\)层的单元数目,\(s_{l+1}\)是第\(l+1\)层的单元数目。\(\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}(\Theta_{ji}^l)^2\)起的作用是将所有的\(i\)、\(j\)和\(l\)的\(\Theta_{ij}\)的值都相加。
Backpropagation algorithm
反向传播算法:让代价函数最小化的算法
Gradient computation
目标:通过寻找合适的\(\Theta\)使\(J(\Theta)\)最小 --> 需要计算\(J(\Theta)\) 和 \(\frac{\part}{\part\Theta_{ij}^{(l)}}J(\Theta)\)。
简单情况:整个训练集只包含一个训练样本(实数对),记为\((x,y)\), 此时计算过程如下:
Forward propagation:
-
\(a^{(1)}\)是第一层的激活值(输入)。
\[a^{(1)} = x \tag1 \] -
计算\(\Theta^{(1)}a^{(1)}\)。
\[z^{(2)} = \Theta^{(1)}a^{(1)} \tag2 \] -
计算第一个隐藏层(神经网络的第二层)的激活值\(a^{(2)}\),同时增加个偏差项。
\[a^{(2)} = g(z^{(2)}) (add a_0^{(2)}) \tag3 \] -
重复上述步骤,直到计算出最后一层\(a^{(4)}\)的值(假设函数的输出)。
\[z^{(3)} = \Theta^{(2)}a^{(2)} \tag4 \]\[a^{(3)} = g(z^{(3)}) (add a_0^{(3)}) \tag5 \]\[z^{(4)} = \Theta^{(3)}a^{(3)} \tag6 \]\[a^{(4)} = h_\Theta(x) = g(z^{(4)}) \tag7 \]
通过向前传播算法,可以计算出每个神经元的激活值。
Backpropagation algotirhm:
-
Intuition: \(\delta_j^{(l)}\) = "error" of node \(j\) in layer \(l\). 第\(l\)层的第\(j\)个结点的误差。
-
初始化:For each output unit (layer L = 4) \(\delta_j^{(4)} = a_j^{(4)} - y_j\) 假设输出和训练集之间的差。
-
向量表示:将\(\delta\)和\(a\)、\(y\)都写为向量的形式,那么计算过程可写为
- \(\delta^{(4)} = a^{(4)} - y\)
- \(\delta^{(3)} = (\Theta^{(3)})^T\delta^{(4)} .* g'(z^{(3)})\)
- \(\delta^{(2)} = (\Theta^{(3)})^T\delta^{(3)} .* g'(z^{(2)})\)
- 注:没有\(\delta^{(1)}\),因为第一次对应输入层,是我们在训练集里观察得到的,所以不会存在误差。
算法表示:
Training set {\((x^{(1)},y^{(1)}),\ldots,(x^{(m)},y^{(m)})\)}
Set \(\Delta_{ij}^{(l)} = 0\) (for all \(l, i, j\)) (used to compte \(\frac{\part}{\part\Theta_{ij}^{(l)}}J(\Theta)\))
For \(i = 1\) to \(m\)
Set \(a^{(1)} = x^{(i)}\) 向前传播
Perform forward propagation to compute \(a^{(l)}\) for \(l = 2, 3, \ldots, L\) 计算出每个结点的激活值
Using \(y^{(i)}\), compute \(\delta^{(L)} = a^{(L)} - y^{(i)}\) 向后传播
Compute \(\delta^{(L-1)},\delta^{(L-2)},\ldots,\delta^{(2)}\) 计算出除第一层外每一层的误差
\(\Delta_{ij}^{(l)} := \Delta_{ij}^{(l)} + a_j^{(l)}\delta_i^{(l+1)}\) 如果写为向量形式则为 \(\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T\)
\(D_{ij}^{(l)} := \frac{1}{m}\Delta_{ij}^{(l)} + \lambda\Theta_{ij}^{(l)}\) if \(j \ne 0\)
\(D_{ij}^{(l)} := \frac{1}{m}\Delta_{ij}^{(l)}\) if \(j = 0\)
最后,可以计算出偏导:\(\frac{\part}{\part\Theta_{ij}^{(l)}}J(\Theta) = D_{ij}^{(l)}\)
Backpropagation intuition
Forward propagation 向前传播算法
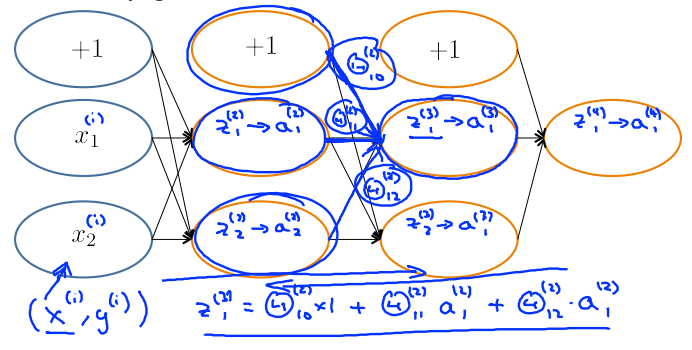
下图所示的神经网络包含两个输入单元,第二层和第三层都有两个输入单元(不算偏差单元),最后的输出层有一个输出单元。
在进行向前传播的过程中,以训练样本\((x^{(i)},y^{(i)})\)为例:\(x^{(i)}\)先被传入到输入层,分别记为\(x^{(i)}_1\)和\(x^{(i)}_2\);传播到第一个隐藏层时,计算输入单元的加权总和\(z_1^{(2)}\)和\(z_2^{(2)}\);将S型逻辑函数和S型激活函数应用到\(z\)的值上,得出激活值\(a_1^{(2)}\)和\(a_2^{(2)}\);再做一次向前传播得到\(z_1^{(3)}\)和\(z_2^{(3)}\);再应用一次S型逻辑函数和S型激活函数,得到\(a_1^{(3)}\)和\(a_2^{(3)}\);最后得到\(z_1^{(4)}\) --> \(a_1^{(4)}\)。
拿\(z_1^{(3)}\)具体看一下,\(z_1^{(3)} = \Theta_{10}^{(2)} \times 1 + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)}\)。
What is backpropagation doing?
\(J(\Theta) = -\frac{1}{m}\left[ \sum_{i=1}^m\sum_{k=1}^Ky_k^{(i)}log( h_\Theta(x^{(i)}))_k + (1-y_k^{(i)})log(1-(h_\Theta(x^{(i)}))_k) \right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}(\Theta_{ji}^l)^2\)
-
Focusing on a single example \(x^{(i)}\), \(y^{(i)}\), the case of \(1\) output unit, and ignoring regularization (\(\lambda = 0\)), \(cost(i) = y^{(i)}logh_\Theta(x^{(i)}) + (1 - y^{(i)})logh_\Theta(x^{(i)})\).
(Think of \(cost(i) \approx (h_\Theta(x^{(i)}) - y^{(i)})^2\)) I.e. how well is the network doing on example i?只有一个输出单元的例子中,如果不考虑正则化(即\(\lambda = 0\)),代价项将由上面的那个式子决定(也可以把\(cost(i)\)想象成神经网络的输出值与实际值差的平方)。这里的\(cost(i)\)代表了神经网络是否能够准确地预测样本\(i\)的值,即输出值和实际观测值\(y^{(i)}\)的接近程度。
-
反向传播是怎么做的呢?一种直观的理解是反向传播算法就是在计算\(\delta_j^{(l)}\)的值(第\(l\)层第\(j\)项的激活值的“误差”)。
Formally, \(\delta_j^{(l)} = \frac{\part}{\part z_j^{(l)}}cost(i)\) (for \(j \geq 0\)), where \(cost(i) = y^{(i)} logh_{\Theta}(x^{(i)}) + (1 - y^{(i)})logh_\Theta(x^{(i)})\)
更正式地说,\(\delta\)实际上是关于\(z_j^{(l)}\)的偏微分,也就是\(cost\)函数关于我们计算出的输入项的加权和。
-
过程分析:拿\(\delta_2^{(2)}\)为例具体看一下,\(\delta_2^{(2)} = \Theta_{12}^{(2)}\delta_1^{(3)} + \Theta_{22}^{(2)}\delta_2^{(3)}\),而\(\delta_2^{(3)}\)又是通过\(\delta_2^{(3)} = \Theta_{12}^{(3)}\delta_1^{(4)}\)得到的。
Implementation note: Unrolling parameters
如何把你的参数从矩阵展开成向量,以便于我们在高级优化中使用。
Advanced optimization
通过执行代价函数costFunction(),输入参数\(\Theta\),返回代价函数以及导数值,再将返回值传递给高级最优化算法,如fminunc()。其中的参数gradient、theta、initialTheta都是以向量的形式出现的。
function [jVal, gradient] = costFunction(theta)
optTheta = fminunc(@costFunction, initialTheta, optopns)
Neural Network (L = 4):
\(\Theta(1)\)、\(\Theta(2)\)、\(\Theta(3)\) - matrices (Theta1, Theta2, Theta2)
\(D^{(1)}\),\(D^{(2)}\),\(D^{(3)}\) - matrices (D1, D2, D3)
对于神经网络,参数不再是向量,而是矩阵了。那么该如何将它们展开成向量呢?
Example
下图为一个输入层10层,隐藏层10层,输出层1层的神经网络。此时\(\Theta\)和\(D\)的维度将由这些表达式确定。
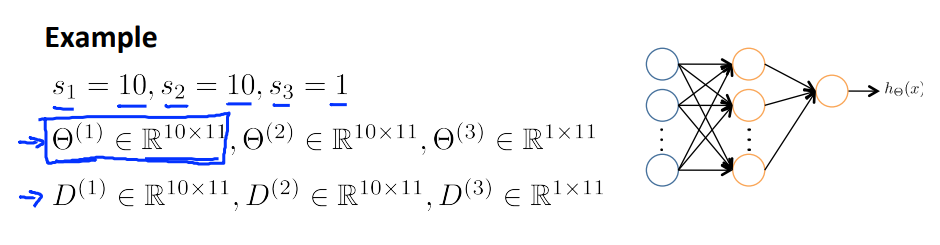
将矩阵转化为向量:
thetaVec = [Theta1(":"); Theta2(":"); Theta3(":")];
DVec = [D1(:); D2(:); D3(:)];
将向量转化为矩阵:
Theta1 = reshape(thetaVec(1:110),10,11);
Theta2 = reshape(thetaVec(111:220),10,11);
Theta3 = reshape(thetaVec(221:231),1,11);
Learning Algorithm
Have initial parameters \(\Theta^{(1)}\),\(\Theta^{(2)}\),\(\Theta^{(3)}\)。
Unroll to get initialTheta to pass to fminunc(@costFunction, initialTheta, options)。
具体过程:
function [jval, gradientVec] = costFunction(thetaVec)
From thetaVec, get \(\Theta^{(1)}\),\(\Theta^{(2)}\),\(\Theta^{(3)}\)。 从参数矩阵中得出\(\Theta\)的值
Use forward prop/back prop to compute \(D^{(1)}\),\(D^{(2)}\),\(D^{(3)}\) and \(J(\Theta)\)。 利用向前传播和向后传播算法计算出导数和代价函数的值
Unroll \(D^{(1)}\),\(D^{(2)}\),\(D^{(3)}\) to get gradientVec。 将导数值展开得到梯度向量并作为函数值返回
Gradient checking 梯度检验
Numerical estimation of gradients 梯度的数值估计
对下图所示的函数\(J(\Theta)\),求他在\(\theta\)处的导数。
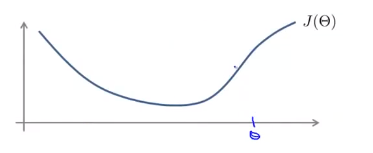
双侧差分法:取一个很小的\(\epsilon\)(如\(10^{-4}\)),令\(\frac{d}{d\Theta}J(\Theta) \approx \frac{J(\Theta + \epsilon) - J(\Theta - \epsilon)}{2\epsilon}\)。
实现:gradApprox = (J(theta + EPSILON) - J(theta - EPSILON)) / (2 * EPSILON)。
以上讨论了\(\theta\)是参数的情况,接下来讨论\(\theta\)是向量时的情况。
Parameter vector \(\theta\)
\(\theta \in R^n\) (E.g. \(\theta\) is "unrolled" vector of \(\Theta^{(1)}\), \(\Theta^{(2)}\), \(\Theta^{(3)}\))\(\theta\)是\(n\)维向量时的情况(如神经网络参数的展开形式)
\(\theta = \theta_1, \theta_2, \theta_3, \ldots, \theta_n\)。 此时,\(\theta\)是一个有\(n\)个元素的\(n\)维列向量。
可以用类似的想法估计所有偏导数项:
思路:
\(\frac{\part}{\part\theta_1}J_\theta \approx \frac{J(\theta_1 + \epsilon,\theta_2,\theta_3\ldots,\theta_n) - J(\theta_1 - \epsilon,\theta_2,\theta_3,\ldots,\theta_n)}{2\epsilon}\)
\(\frac{\part}{\part\theta_2}J_\theta \approx \frac{J(\theta_1,\theta_2 + \epsilon,\theta_3\ldots,\theta_n) - J(\theta_1,\theta_2 - \epsilon,\theta_3,\ldots,\theta_n)}{2\epsilon}\)
\(\vdots\)
\(\frac{\part}{\part\theta_n}J_\theta \approx \frac{J(\theta_1,\theta_2,\theta_3\ldots,\theta_n + \epsilon) - J(\theta_1,\theta_2,\theta_3,\ldots,\theta_n - \epsilon)}{2\epsilon}\)
实现:
for i = 1 : n,
thetaPlus = theta;
thetaPlus(i) = thetaPlus(i) + EPSILON;
thetaMinus = theta;
thetaMinus(i) = thetaMinus(i) - EPSILON;
gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2 * EPSILON);
end;
Check that gradApprox ≈ DVec 确定估计出的导数是否近似等于反向传播得出的导数
Implementation Note 总体步骤
- Implement backprop to compute
DVec(unrolled \(D^{(1)}\),\(D^{(2)}\),\(D^{(3)}\)). 利用向后传播算法计算\(D^{(1)}\),\(D^{(2)}\),\(D^{(3)}\)。 - Implement numerical gradient check to compute
gradApprox. 计算出gradApprox。 - Make sure they give similar values. 确定上面两者结果近似
- Turn off gradient checking. Using backprop code for learning. 关掉梯度检验,使用反向传播算法。
Important
Be sure to disable your gradient checking code before training your classifier. If you run numerical gradient computation on every iteration of gradient descent (or in the inner loop of costFunction(...)) your code will very slow.
一定要在开始训练你的分类器之前将梯度检验的代码关闭,因为它是一个非常慢的计算近似导数的方法。验证完反向传播算法的正确性之后,梯度检验程序就可以关闭了。
Random initialization 随机初始化
Initial value of \(\Theta\)
For gradient descent and advanced optimization method, need initial value for \(\Theta\).
对于梯度下降算法或者其它的一些高级优化算法,需要一个初始的\(\Theta\)值。
optTheta = fminunc(@costFunction, initialTheta, options)
Consider gradient descent 考虑梯度下降算法
Set initialTheta = zero(n, 1)? 初始化为0是否可行?
Zero initialization
以图示神经网络为例,如果所有变量初始化为0,即输入层和隐藏层之间的连线的权值均为0,则这两个隐藏单元会对输入值进行相同的计算,最终得到相同的结果(\(a_1^{(2)} = a_2^{(2)}\))。
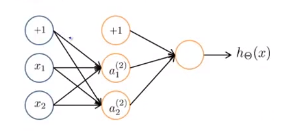
After each update, parameters corresponding to inputs going into each of two hidden units are identical. 每次更新后,与输出到两个隐藏单元中的,第一层每个单元中的输入对应的参数是相同的。即\(\delta_1^{(2)} = \delta_2^{(2)}\)、\(\frac{\part}{\part\Theta_{01}^{(1)}}J(\Theta) = \frac{\part}{\part\Theta_{02}^{(1)}}J(\Theta)\)、\(\Theta_{01}^{(1)} = \Theta_{02}^{(1)}\)。
为了解决这一问题,神经网络初始化的方式采用随机初始化.
Random initialization: Symmetry breaking
上面出现的问题有时被我们称为对称权重的问题(所有的权值相同),所以在种初始化解决的是如何打破这种对称性。
Initialize each \(\Theta_{ij}^{(l)}\) to a random value in \([-\epsilon,\epsilon]\) (i.e. \(-\epsilon \leq \Theta_{ij}^{(l)} \leq \epsilon\)) 对\(\Theta\)的每个值进行初始化,范围在\([-\epsilon,\epsilon]\)内。
代码实现:
Theta1 = rand(10, 11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(1, 11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Summery 总结
为了训练神经网络,应该对权值进行随机初始化:将\(\Theta\)初始化为\([-\epsilon,\epsilon]\)的一个数,然后进行反向传播,执行梯度检查,使用梯度下降或者其他先进的优化算法最小化\(J(\Theta)\)的值。
变量\(\Theta\)的功能从任意选择变量的初始值开始,通过打破对称性这一进程,达到梯度下降或是其他先进的优化算法可以找到\(\Theta\)的最优值的目的。
Putting it together
这些零散的内容相互之间有什么联系以及神经网络学习算法的总体实现过程。
Training a neural network
Pick a network architecture (connectivity pattern between neurons) 搭建网络框架(神经元之间的连接模式)
考虑的问题:选择多少个隐藏层,每个隐藏层可以选择多少个隐藏单元。
输入/输出单元的个数:
-
No. of input units: Dimension of features \(x^{(i)}\). 输入单元的数量:特征集\(x\)对应的输入单元的数目(特征\(x\)的维度)。
-
No. of output units: Number of classes. 输出单元的数目:(多分类问题中)所要区分的类别个数。
隐藏层单元/隐藏层的个数:
Reasonable default: 1 hidden layer, or if \(\gt\) 1 hidden layer, have same no. of hidden units in every layer (usually the more the better)
-
默认的规则是只使用单个隐藏层,所以下图中最左边表示的这种只有一个隐藏层的神经网络一般来说是最普遍的。
-
如果使用不止一个隐藏层的话,也有一个默认规则,就是每个隐藏层通常都应有相同的单元数。
-
对于隐藏单元的个数,通常是越多越好。
-
每个隐藏层所包含的单元数量,还应和输入\(x\)的维度相匹配,也要和特征的数目匹配。

神经网络的训练过程:
-
Randomly initialize weights 随机初始化权值
-
Implement forward propagation to get \(h_\Theta(x^{(i)})\) for any \(x^{(i)}\) 执行向前传播算法,对每一个\(x^{(i)}\)计算出对应的\(h_\Theta(x^{(i)})\)(即输出值\(y\)的向量)
-
Implement code to compute cost function \(J(\Theta)\) 计算出代价函数
-
Implement backprop to compute partial dervatives \(\frac{\part}{\part\Theta_{jk}^{(l)}}J(\Theta)\) 执行反向传播算法来求出偏导数/偏微分项
for i = 1 : m Perform forward propagation and backpropagation using example (\(x^{(i)},y^{(i)}\)) (Get activations \(a^{(l)}\) and delta terms \(\delta^{(l)}\) for \(l = 2, \ldots, L\)). 对每一个\(x^{(i)},y^{(i)}\)执行向前传播算法和向后传播算法得到激活值\(a^{(l)}\)和\(\delta\)项。
-
Use gradient checking to compare \(\frac{\part}{\part\Theta_{jk}^{(l)}}J(\Theta)\) computed using backpropagation vs. using numerical estimate of gradient of \(J(\Theta)\). 用梯度检验程序检验已经计算得到的偏导数项是否存在误差过大的问题
Then disable gradient checking code. 完成后关闭梯度检验程序
-
Use gradient descent or advanced optimization method with backpropagation to try to minimize \(J(\Theta)\) as a function of parameters \(\Theta\). 将一个最优化算法(如梯度下降算法)与反向传播算法相结合,从而得出偏导数项的值。
Autonomous driving example
神经网络的应用之自动驾驶汽车。
Review
测验:
-
You are training a three layer neural network and would like to use backpropagation to compute the gradient of the cost function. In the backpropagation algorithm, one of the steps is to update \(\Delta^{(2)}_{ij} := \Delta^{(2)}_{ij} + \delta^{(3)}_i * (a^{(2)})_j\) for every i, j. Which of the following is a correct vectorization of this step?
-
Suppose \(\Theta_1\) is a 5x3 matrix, and \(\Theta_2\) is a 4x6 matrix. You set
thetaVec=[Theta1(:);Theta2(:)]. Which of the following correctly recovers \(\Theta_2\)? -
Let \(J(\theta) = 2 \theta^3 + 2\). Let \(\theta=1\), and \(\epsilon = 0.01\). Use the formula \(\frac{J(\theta + \epsilon) - J(\theta - \epsilon)}{2\epsilon}\) to numerically compute an approximation to the derivative at \(\theta=1\). What value do you get? (When \(\theta = 1\), the true/exact derivati ve is \(\frac{dJ(\theta)}{d\theta} = 6\).)
-
Which of the following statements are true? Check all that apply.
-
Which of the following statements are true? Check all that apply.
编程:
-
nnCostFunction.m
a1 = [ones(m, 1) X]; z2 = a1 * Theta1'; a2 = sigmoid(z2); a2 = [ones(m, 1) a2]; z3 = a2 * Theta2'; a3 = sigmoid(z3); h = a3; yk = zeros(m, num_labels); for i = 1 : m yk(i, y(i)) = 1; end; J = 1 / m * sum(sum(-yk .* log(h) - (1 - yk) .* log(1 - h))); X = [ones(m, 1) X]; -
nnCostFunction.m
sum1 = sum(sum(Theta1(:,2:end) .^ 2)); sum2 = sum(sum(Theta2(:,2:end) .^ 2)); r = lambda / (2 * m) * (sum1 + sum2); J = J + r; -
sigmoidGradient.m
g = sigmoid(z) .* (1 - sigmoid(z)); -
randInitializeWeights.m
epsiolon_init = 0.12; W = rand(L_out, 1 + L_in) * 2 * epsiolon_init - epsiolon_init; -
nnCostFunction.m
Theta1_grad = 1 / m * Delta1 + lambda / m * Theta1; Theta2_grad = 1 / m * Delta2 + lambda / m * Theta2; Theta1_grad(:,1) = Theta1_grad(:,1) - lambda / m * Theta1(:,1); Theta2_grad(:,1) = Theta2_grad(:,1) - lambda / m * Theta2(:,1); -
nnCostFunction.m
delta3 = a3 - yk; delta2 = delta3 * Theta2; delta2 = delta2(:,2:end); delta2 = delta2 .* sigmoidGradient(z2); Delta1 = zeros(size(Theta1)); Delta2 = zeros(size(Theta2)); Delta1 = Delta1 + delta2' * a1; Delta2 = Delta2 + delta3' * a2;


