实验与统计学

从实验的过程上来看，好像不涉及统计的相关的内容，但统计学对实验的效果非常重要，决定了是否可以信任最终的实验结果，以及是否可以做出正确的决策

AB实验中涉及到统计知识如下图，主要围绕图中来介绍这些概念和AB实验的关系

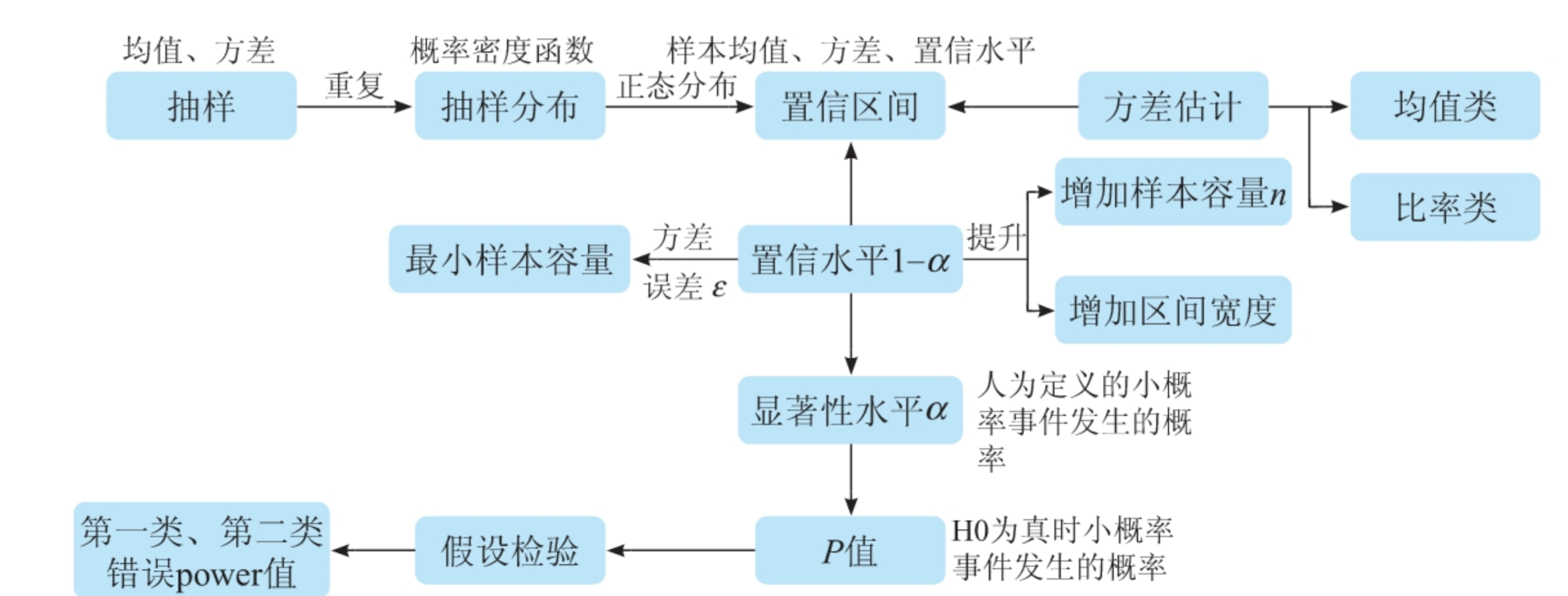
1. 抽样分布

1.1 抽样

如果我们想知道所有用户的平均APP停留时长，可以把所有用户APP停留时长加起来除以用户数，这在互联网应用中是可以实现的

但如果我们想知道山西人平均身高，要把所有人的身高都去测量一遍，基本不可实现，所以这时候可以采用抽样的方法，我们从山西省内找10000个人来测他们的平均值

抽样的思想是使用样本的指标代表总体的指标

在上面的例子中：

• 总体为所有山西人
• 样本为10000个山西人
• 指标为平均身高

1.1.1 均值

上面的平均身高和平均APP停留时长是均值指标，某些场景会用均值指标来代表数据好坏，假如山西平均身高为170cm，你的身高为178cm，那你在山西人里面算高的。 有些场景则不太适用，例如收入场景，网友们经常抱怨自己的收入被平均了

\[\bar{x} = \frac{\sum_{i=1}^nx_i}{n} \]

1.1.2 方差

各个数据离平均值的距离，代表了数据的离散程度，值越大，代表越离散。越离散抽样越不具有代表性

总体方差：

\[\sigma^2 = \frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n} \]

样本方差（总体方差的无偏估计）：

\[S^2 = \frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n-1} \]

1.1.1 抽样和AB实验的关系

在做AB实验时，我们一般不会选择整体用户，而是选择一定比例的流量，例如10%，那么其实就是对用户进行抽样，用10%的流量来预估总体

在确认实验效果时，通常会看均值类指标（例如平均停留时长）和比率类指标（点击率）等

1.2 抽样分布

抽样分布是样本统计量的分布，样本统计量是样本的平均值和样本率

每抽取一组样本都可以计算出一个样本均数，把这些样本均数出现的次数绘制成一幅图就是它的分布

常见的分布有：

• 正态分布
• 卡方分别
• t分布
• f分布

1.2.1 概率密度函数

把随机变量出现的值和次数绘制成一幅图，就可以看到这个随机变量出现某个值的概率，也就是它的分布图

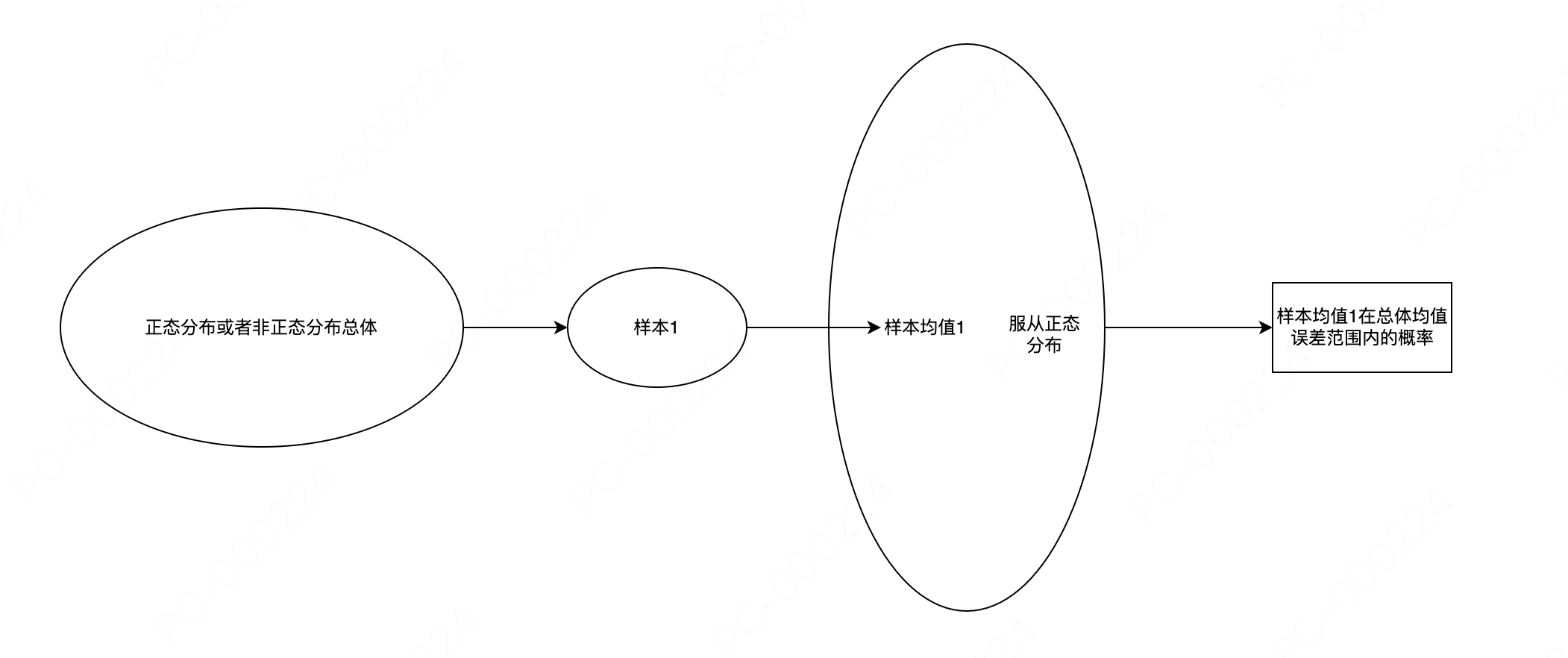
1.2.2 抽样分布和AB实验的关系

1.2.1.1 衡量置信水平

抽样是用样本来预估总体

那比如我们现在有随机抽取了10%流量的用户的平均停留时长是5分钟，那么能得出整体的平均停留时长也是5分钟吗？

背后的原理是抽样分布和中心极限定理，简单来讲正态分布的样本均值是可以代表总体均值的，

但实际中我们也不会真的抽样很多次，AB实验我们也就是抽样了一次，我们最终会估计样本均值在误差范围内的置信度

1.2.1.2 SRM校验

Sample Ratio Mismatch，样本比例不匹配，举个例子，假如有10000个用户，2个实验组，那么理论情况每个分组会有5000个用户

现在实际情况是4982和5021，那这两组分的均匀吗？看起来是均匀的；又比如是3000和7000，看起来不均匀，为了避免使用直觉来判断，所以需要来做SRM校验，卡方适合度校验会告诉我们4850和4750这样的分流是不是均匀的

from scipy.stats import chisquare,chi2

observed_data = [48890, 51110]
expected_data = [50000, 50000]
chi_square_test_statistic, p_value = chisquare(
    observed_data, expected_data)

# chi square test statistic and p value
print('chi_square_test_statistic is : ' +
      str(chi_square_test_statistic))
print('p_value : ' + str(p_value))
print(chi2.ppf(1-0.05, df=6))

# chi_square_test_statistic is : 49.284
# p_value : 2.2146145229918383e-12
# 12.591587243743977


observed_data = [49890, 50110]
expected_data = [50000, 50000]

# chi_square_test_statistic is : 0.484
# p_value : 0.4866160457640505
# 12.591587243743977

p值<0.05,于是我们认为分组存在显著差异，出现了SRM的问题

2. 置信区间

点估计：样本均值来代表总结均值

抽样误差：对于同一个总体，两波样本可能得出两个差异比较大的样本均数，那到底哪个均数估计的更准呢？

\[抽样误差 = |\bar{x}-\mu| \]

我们可以根据抽样误差和样本均值来计算总体均值\(\mu\)

区间估计：

\[\bar{x}-抽样误差 < \mu < \bar{x}+抽样误差 \]

对于正态分布数据，95%的数据都在总体均值的1.96个标准差内

\[\bar{x}-1.96\frac{\sigma}{\root \of n} < \mu < \bar{x}+1.96\frac{\sigma}{\root \of n} \]

其中\(\frac{\sigma}{\root \of n}\) 是样本均值标准差，通过这样的方式，我们用区间来代替了点估计，使数据更加可信，这里的含义是总体均值95%的概率在这个区间范围内

2.1 方差（标准差）估计

在算置信区间的时候，我们使用了总体标准差\(\sigma\)来算样本均值标准差\(\frac{\sigma}{\root \of n}\)，而实际的应用中往往无法得知总体标准差，需使用样本标准差S来代替总体标准差

对于均值类指标样本标准差为，其中n-1是用来减少样本数量少于总体时标准差的误差，正常应该是n：

\[S^2 = \frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n-1} \]

对于比率类指标，具体可以参考01分布和二项分布相关内容：

\[S^2 = p(1-p) \]

上面其实是只有一个样本时的计算公式，而在AB实验中，我们有对照组和实验组两个样本，其方差是两个样本的总体方差，

均值类指标为：

\[S^2 = \frac{(n_1-1)\sum_i^{n_1}(x_i-\bar{x_1})^2 + (n_2-1)\sum_i^{n_2}(x_i-\bar{x_2})^2}{n_1+n_2-2} \]

比率类指标为：

\[S^2 = p_1(1-p_1) + p_2(1-p_2) \]

2.2 置信水平1-α

在讲置信区间的时候，讲了95%的数据都在总体均值的1.96个标准差内，为什么要选95%呢？这个对应α是5%，也就是0.05，也叫显著性水平

显著性水平如果变大，例如为0.1，那么我们犯错误的概率会变高，因为总体均值只有90%的概率在这个区间范围内

显著性水平如果变小，例如为0.01，那么我们犯错误的概率会变小，但是相应的，我们需要更多的样本量

2.3 统计功效1-β

置信水平1-α 避免把没有效果的实验当成有效果的实验，而统计功效1-β正好相反，避免把有效果的实验当成没效果的实验

	含义	常用值
α	犯第一类错误的概率，即无用认为有用，影响严重	5%
β	犯第二类错误的概率，即有用认为无用，影响比较轻微	20%

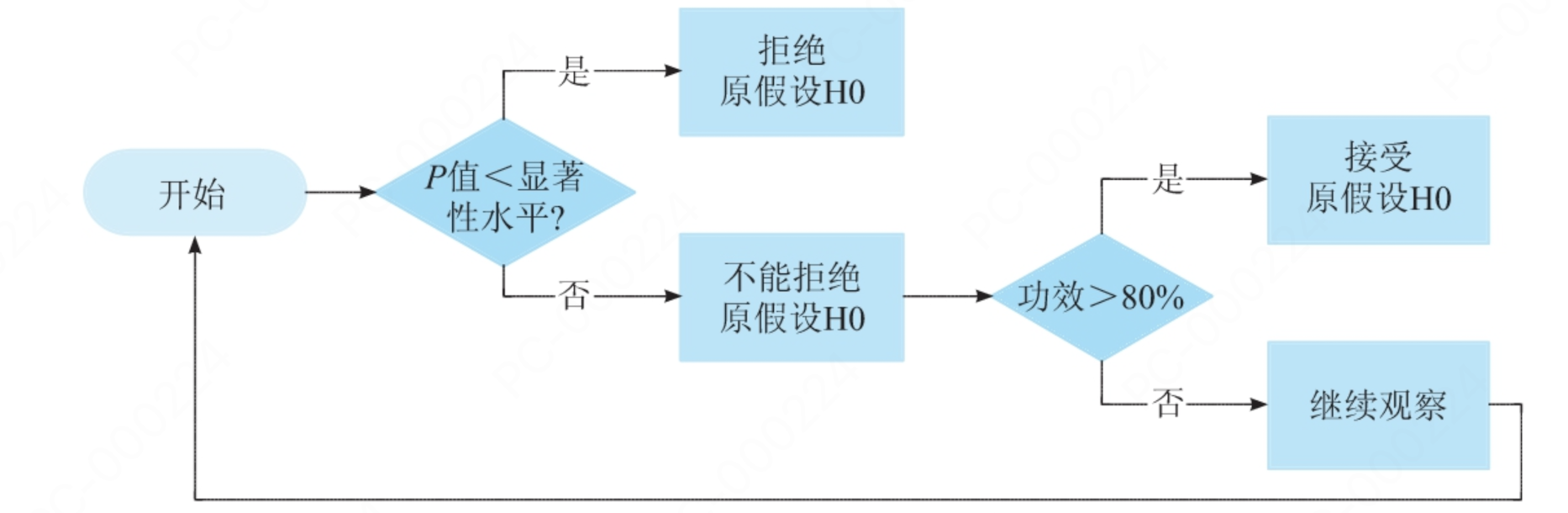
2.4 置信区间和AB实验的关系

2.4.1 样本量估计

使用样本来预估总体，那么取多少样本合适呢，太少代表不了总体，100位同学的平均身高代替1000万同学的平均身高，感觉误差会比较大，那么多少合适呢？

2.4.1.1 单样本

基本公式，如何推导的

\[n = \frac{2(Z_{1-\frac{\alpha}{2}} + Z_{1-\beta})^2\sigma^2}{\epsilon^2} \]

• Z 为正态分布的分位数函数
• \(\epsilon\)代表两组数据的差值，例如停留时长均值提升5分钟，转化率提升10%等
• \(\sigma\) 代表方差，上面已经讲过不同类指标的估计方式

2.4.1.2 多样本

因为AB实验是多个分组，所以需要2n的总样本量，根据不同的指标类型代入不同的方差

3. 假设检验

假设检验是先对总体参数提出一个假设值，然后利用样本信息判断这一假设是否成立

举个栗子，仍以点击率为例，我们运行AB测试一周，分别对1000个样本进行了测试。对照组A的点击率为7.5%，B的点击率为9%，如下表：

我们能否给出结论说B比A好，改动是有效果的呢？有多大的可能是因为一些随机的因素导致这样的差异呢？

3.1 Z检验

Z检验是一种适用于大样本（样本容量大于30）的两组平均数之间差异显著性检验的方法。它是通过计算两组平均数之间差的Z值与理论Z值相比较，看是否大于规定的理论Z值，从而判定两组平均数的差异是否显著。

其一般步骤如下：

第一步：建立原假设 H0:μ1 = μ2 ，即先假定两组平均数之间没有显著差异，

第二步：计算统计量Z值，对于不同类型的问题选用不同的统计量计算方法，通过检验两组样本平均数的差异性，判断它们各自代表的总体的差异是否显著。

与计算样本量相似，当观测的指标为绝对值类型/比率型指标时，Z值的计算公式有所差异。

当观测指标为绝对值类指标时

\[Z = \frac{\bar{X_A}-\bar{X_B}}{\sqrt{\frac{\sigma_A^2}{N_A}+\frac{\sigma_B^2}{N_B}}} \]

当观测指标为比率类指标时

\[Z = \frac{P_A-P_B}{\sqrt{\frac{P_A(1-P_A)}{N_A}+\frac{P_B(1-PB)}{N_B}}} \]

假设通过以上公式计算的统计量Z值 = 1.22，小于我们设定95%置信水平对应理论Z值1.96，也就是说我们暂无法判断这种差异性是显著的，所以上述样本不足以得出B比A好的结论

3.2 假设检验和AB实验的关系

3.2.1 AA实验

可以判断AA实验的两组流量是否无差异，为什么需要验证，因为如果原本的两组流量就有差异，那么在实验完成之后，很难得出是新策略的影响，还是原本的影响

当然，为了避免花费更多的实验去做实验，可以使用之前的数据进行分析

3.2.2 AB实验

可以验证AB实验是否有效果差异，这也是做AB实验的最终目的，通过验证得到统计学上面的差异，避免通过人工的方式判断失误，例如在一段时间内差异很大就认为有差异，又例如差异不明显就认为没差异，可以通过更规范的手段获取更正确的决策

4. 总结

本文介绍了一些AB实验中的统计学基本概念和相互关系，AB实验背后的原理是基于这些统计学知识，了解这些无论是在设计AB实验系统，还是在日常AB实验中，都有帮助

参考

字节跳动 A/B 实验背后的秘密：样本量计算

抽样好懂，抽样分布却是在说啥

怎样全面理解95%置信区间

神策-试验样本预估指南

AB测试系列 - AB测试里的统计学 PART 2

假设检验——这一篇文章就够了