RSA，DH，DSA

RSA

RSA公开密钥密码体制。

所谓的公开密钥密码体制就是使用不同的加密密钥与解密密钥，是一种“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。

在公开密钥密码体制中，加密密钥（即公开密钥）PK是公开信息，而解密密钥（即秘密密钥）SK是需要保密的。

加密算法E和解密算法D也都是公开的。

虽然秘密密钥SK是由公开密钥PK决定的，但却不能根据PK计算出SK。它通常是先生成一对RSA 密钥，其中之一是保密密钥，由用户保存；另一个为公开密钥，可对外公开，甚至可在网络服务器中注册。

 

步骤

1. Choose two distinct prime numbers p and q. 【两个大质数】
   • For security purposes, the integers p and q should be chosen at random, and should be of similar bit-length. Prime integers can be efficiently found using a primality test.
2. Compute n = pq. 【n是两个大质数p、q的积】
   • n is used as the modulus for both the public and private keys
3. Compute φ(n) = (p – 1)(q – 1), where φ is Euler's totient function.
4. Choose an integer e such that 1 < e < φ(n) and greatest common divisor of (e, φ(n)) = 1; i.e., e and φ(n) are coprime. 【e 和 φ(n) 互质】
5. e is released as the public key exponent. 【e是公钥匙】
6. e having a short bit-length and small Hamming weight results in more efficient encryption - most commonly 0x10001 = 65,537. However, small values of e (such as 3) have been shown to be less secure in some settings.^[4]
7. Determine d as:

i.e., d is the multiplicative inverse of e mod φ(n).

• This is more clearly stated as solve for d given (de) mod φ(n) = 1
• This is often computed using the extended Euclidean algorithm.
• d is kept as the private key exponent. 【d是秘匙】

加密

Alice transmits her public key to Bob and keeps the private key secret.

He first turns M into an integer m, such that by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext corresponding to

.  

 

解密

Alice can recover 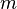from by using her private key exponent via computing

.  

Given 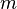, she can recover the original message M by reversing the padding scheme.

 

RSA的安全性依赖于大数分解，因此，模数n 必须选大一些，因具体适用情况而定。

由于进行的都是大数计算，使得RSA最快的情况也比DES慢上好几倍，无论是软件还是硬件实现。速度一直是RSA的缺陷。一般来说只用于少量数据加密。

 

http://baike.baidu.com/view/7520.htm

http://en.wikipedia.org/wiki/RSA_(algorithm)

 

DH

Alice				Bob
Secret	Public	Calculates	Sends	Calculates	Public	Secret
a	p, g		p,g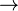			b
a	p, g, A	ga mod p = A	A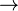		p, g	b
a	p, g, A		B	gb mod p = B	p, g, A, B	b
a, s	p, g, A, B	Ba mod p = s		Ab mod p = s	p, g, A, B	b, s

 

 

安全性：

Diffie-Hellman密钥交换算法的安全性依赖于这样一个事实：虽然计算以一个素数为模的指数相对容易，但计算离散对数却很困难。对于大的素数，计算出离散对数几乎是不可能的。

在选择了合适的G和g时，这个协议被认为是窃听安全的。

如果Alice和Bob使用的随机数生成器不能做到完全随机并且从某种程度上讲是可预测的，那么Eve的工作将简单的多。

 

身份验证

在最初的描述中，迪菲－赫尔曼密钥交换本身并没有提供通讯双方的身份验证服务，因此它很容易受到中间人攻击。 一个中间人在信道的中央进行两次迪菲－赫尔曼密钥交换，一次和Alice另一次和Bob，就能够成功的向Alice假装自己是Bob，反之亦然。而攻击者可以解密（读取和存储）任何一个人的信息并重新加密信息，然后传递给另一个人。因此通常都需要一个能够验证通讯双方身份的机制来防止这类攻击。

 

 

优缺点：

1、 仅当需要时才生成密钥，减小了将密钥存储很长一段时间而致使遭受攻击的机会。

2、 除对全局参数的约定外，密钥交换不需要事先存在的基础结构。

 

然而，该技术也存在许多不足：

1、 没有提供双方身份的任何信息。

2、 它是计算密集性的，因此容易遭受阻塞性攻击，即对手请求大量的密钥。受攻击者花费了相对多的计算资源来求解无用的幂系数而不是在做真正的工作。

3、 没办法防止重演攻击。

4、 容易遭受中间人的攻击。第三方C在和A通信时扮演B；和B通信时扮演A。A和B都与C协商了一个密钥，然后C就可以监听和传递通信量。中间人的攻击按如下进行：

（1） B在给A的报文中发送他的公开密钥。

（2） C截获并解析该报文。C将B的公开密钥保存下来并给A发送报文，该报文具有B的用户ID但使用C的公开密钥YC，仍按照好像是来自B的样子被发送出去。A收到C的报文后，将YC和B的用户ID存储在一块。类似地，C使用YC向B发送好像来自A的报文。

（3） B基于私有密钥XB和YC计算秘密密钥K1。A基于私有密钥XA和YC计算秘密密钥K2。C使用私有密钥XC和YB计算K1，并使用XC和YA计算K2。

（4） 从现在开始，C就可以转发A发给B的报文或转发B发给A的报文，在途中根据需要修改它们的密文。使得A和B都不知道他们在和C共享通信。

 

http://en.wikipedia.org/wiki/Diffie-Hellman_key_exchange

 

DSS/DSA算法

　　Digital Signature Algorithm
　　(DSA)是Schnorr和ElGamal签名算法的变种，被美国NIST作为DSS(Digital SignatureStandard)。算法中应用了下述参数：
　　p：L bits长的素数。L是64的倍数，范围是512到1024；
　　q：p - 1的160bits的素因子；
　　g：g = h^((p-1)/q) mod p，h满足h < p - 1, h^((p-1)/q) mod p > 1；
　　x：x < q，x为私钥 ；
　　y：y = g^x mod p ，( p, q, g, y )为公钥；
　　H( x )：One-Way Hash函数。DSS中选用SHA( Secure Hash Algorithm )。
　　p, q,
　　g可由一组用户共享，但在实际应用中，使用公共模数可能会带来一定的威胁。签名及验证协议如下：
　　1. P产生随机数k，k < q；
　　2. P计算 r = ( g^k mod p ) mod q
　　s = ( k^(-1) (H(m) + xr)) mod q
　　签名结果是( m, r, s )。
　　3. 验证时计算 w = s^(-1)mod q
　　u1 = ( H( m ) * w ) mod q
　　u2 = ( r * w ) mod q
　　v = (( g^u1 * y^u2 ) mod p ) mod q
　　若v = r，则认为签名有效。
　　DSA是基于整数有限域离散对数难题的，其安全性与RSA相比差不多。DSA的一个重要特点是两个素数公开，这样，当使用别人的p和q时，即使不知道私钥，你也能确认它们是否是随机产生的，还是作了手脚。RSA算法却作不到。