堆排序

一、简介

堆排序可以分为两个阶段：构造堆和下沉排序两个阶段。

构造堆：将原始数组重新组织为一个堆。

下沉排序：从堆中按递减顺序取出所有元素并得到排序结果。

 

二、实现

1、堆排序

中规中矩的方法：

从左向右遍历整个数组，用swim方法保证当前位置左侧的所有元素已经是堆有序的即可。

就像连续向优先队列中插入元素一样。可以在NlogN成正比的时间内完成这个任务。

 

更加高效的方法：

从右至左用sink方法构造子堆，数组的每个位置都是一个子堆的根节点，sink对这些子堆也适用。

如果一个节点的两个子节点都是堆的根节点了，那么对该节点调用sink函数可以将以这个节点为根节点的树变为堆。

这个过程会递归地建立起堆的秩序。这个过程只需扫描数组中的一半元素，因为大小为1的子堆可以跳过。

 

2、下沉排序

将堆最大的元素删除，然后放入堆缩小后数组中空出的位置。

 

 代码实现如下：

    public static void sort(Comparable[] pq) {
        int n = pq.length;
        for (int k = n/2; k >= 1; k--)
            sink(pq, k, n);
        while (n > 1) {
            exch(pq, 1, n--);
            sink(pq, 1, n);
        }
    }

 

 

基础函数：

　　/***************************************************************************
    * Helper functions to restore the heap invariant.
    ***************************************************************************/

    private static void sink(Comparable[] pq, int k, int n) {
        while (2*k <= n) {
            int j = 2*k;
            if (j < n && less(pq, j, j+1)) j++;
            if (!less(pq, k, j)) break;
            exch(pq, k, j);
            k = j;
        }
    }

   /***************************************************************************
    * Helper functions for comparisons and swaps.
    * Indices are "off-by-one" to support 1-based indexing.
    ***************************************************************************/
    private static boolean less(Comparable[] pq, int i, int j) {
        return pq[i-1].compareTo(pq[j-1]) < 0;
    }

    private static void exch(Object[] pq, int i, int j) {
        Object swap = pq[i-1];
        pq[i-1] = pq[j-1];
        pq[j-1] = swap;
    }

 

 

尽管sort函数中，两个循环任务不同，第一个循环构造堆，第二个循环在下沉排序中销毁堆。

这两个循环都是基于sink方法，这个实现跟优先队列的API区分开来是为了突出这个排序算法的简洁性。

 

三、性能分析

结论1：用下沉sink操作构造N个元素堆，只需要少于2N次比较以及少于N次交换。

证明：http://algs4.cs.princeton.edu/24pq/

It suffices to prove that sink-based heap construction uses fewer than n exchanges because the number of compares is at most twice the number of exchanges. For simplicity, assume that the binary heap is perfect (i.e., a binary tree in which every level is completed filled) and has height h.

 

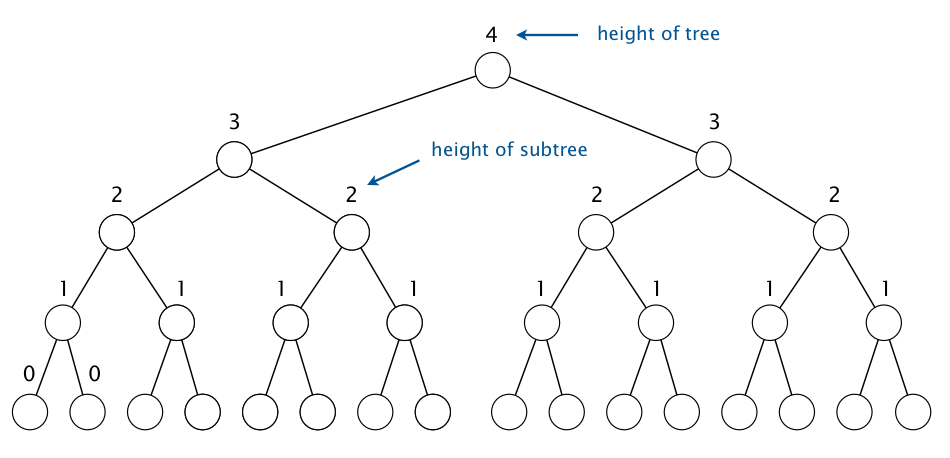
We define the height of a node in a tree to be the height of the subtree rooted at that node. A key at height k can be exchanged with at most k keys beneath it when it is sunk down. Since there are 2^h−k nodes at height k, the total number of exchanges is at most:

 

The first equality is for a nonstandard sum, but it is straightforward to verify that the formula holds via mathematical induction. The second equality holds because a perfect binary tree of height h has 2^h+1 − 1 nodes.

Proving that the result holds when the binary tree is not perfect requires a bit more care. You can do so using the fact that the number of nodes at height kin a binary heap on n nodes is at most ceil(n / 2^k+1).

 

结论2：将N个元素排序，堆排序只需少于（2NlogN + 2N）次比较，以及少于一半次数（NlogN + N）的交换。

证明：

2N项来源于堆的构造，证明看结论1。

2NlogN来源于每次下沉操作最大可能2logn（1 <= n <= N-1）次比较。即2*（logN-1 + log N-2 + …… + log1）~2NlogN

 

结论3：堆排序在排序复杂性的研究中有有重要的地位。

堆排序是唯一能够同时最优地利用空间和时间的方法。在最坏的情况也能保证~2NlogN次比较和常数级别额外空间。

但是，堆排序无法利用缓存，堆排序中数组元素很少与相邻的其他元素进行比较，因此缓存未命中的概率远远大于大多数比较都在相邻元素之间的算法。