时间序列ARIMA模型预测方法，及相关函数使用方法介绍
一、概述
首先引入Daniel检验的概念，即检测序列平稳性的一种方法，它是建立在Spearman相关系数（一种秩相关系数）的基础上的。
对于二维总体（X，Y）的样本观测数据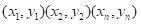
，其中各分量
、
..
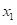的秩统计量为R1、R2…Rn,y1,y2..yn的秩统计量为S1、S2…Sn。
推广到时间序列预测样本，Spearman的相关系数为：
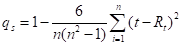
构造统计量：
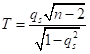
对于给定的alpha,通过t分布表可以查得
的值，如果统计量大于查表的值，则接受检验假设H0: =0,即序列平稳，可以准确预测，否则拒绝H0，序列不平稳。
二、时间序列预测的优缺点分析
（一）优点：
根据过去的事物发展规律预测将来，对于波动不大的事物变化，有较为精确的预测性。适合用于预测经济类等波动不明显的问题。
（二）缺点：
如果事物的发展规律波动较大，Spearman相关系数的假设检验不通过，T检验值大于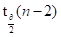
，序列不平稳，预测值出现较大误差。
三、ARIMA时间序列预测实例：
MATLAB代码：
1 %% 时间序列预测法 2 clc,clear all; 3 a = [15.2 15.9 18.7 22.4 26.9 28.3 30.5 33.8 40.4 50.7 58 66.7 81.2 83.4]; 4 Rt = tiedrank(a) %求原始序列的秩统计量、(即将原始数据(因变量)从小到大排列) 5 n = length(a); 6 t = 1:n; 7 disp('Qs:') 8 Qs = 1-6/(n*(n^2-1))*sum((t-Rt).^2) %di=Ri（自变量的秩统计量）-Si（因变量的秩统计量）,即为di=t-Rt 9 T = Qs*sqrt(n-2)/sqrt(1-Qs.^2); 10 t_0 = tinv(0.975,n-2) %计算alpha/2的值 11 b = diff(a) %求原始序列的一阶差分 12 m = ar(b,2,'ls') %估计标量时间序列的AR模型参数,option为最小二乘法 13 %仅用于标量时间序列。对于多变量数据，请使用arx。 14 disp('原始数据的预测值（第二个参数必须为列向量）：') 15 bhat = predict(m,b') 16 disp('计算一个预测值（第二个参数必须为列向量）：') 17 bhat(end+1) = forecast(m,b',1) 18 ahat = [a(1),a+bhat'] %原始数据预测值 19 delta = abs((ahat(1:end-1)-a)./a) %相对误差
四、模型推广及复用
