Lecture16_光线追踪4（Ray Tracing 4）_GAMES101 课堂笔记

上节课内容：

本节课内容：

一、蒙特卡罗积分（Monte Carlo Integration）

why : 对于一些很难写出解析式的曲线，很难求其积分。因此引入蒙特卡罗积分计算。

What & How：通过平均函数值的随机样本估计整体功能的（计算每个采样点 x 对应的函数值 f(x)（长方形的高） \(\times\) 区间长度 [a,b]。将所有的长方形面积求和再求平均——即为该积分值）。具体的理解步骤如下：

some notes：

1. The more samples, the less variance.
2. Sample on x, integrate on x.

---

二、路径追踪（Path Tracing）

（一） 路径追踪引入

why :因为对于 Whitted-Style 光线追踪有下面两个问题：

问题1 —— 总是执行镜面反射

比如上面这个“犹他茶壶”，对于左图表现为镜面反射当然没有问题；但是对于右边的磨砂材质，如果使用光线追踪依旧是按照镜面反射进行，会得到与左图同样的结果。显然是错误的。

问题2 —— 在漫反射表面停止弹射

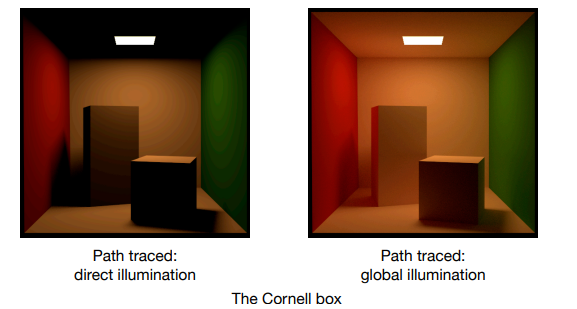
比如，对于左图是使用光线追踪直接光照产生的效果，可以看见箱子靠墙的一面为黑色；但是对于右图中箱子靠墙的一面分别表现为红色、绿色，这就是对漫反射光线继续进行弹射（bounce）的结果（更符合现实）。

“The Cornell box” 常被用于测试全局光照。

（二）求解 Whitted-style Ray Tracing

因此，这样来看某种程度上Whitted-style Ray Tracing是错误的，但是他的渲染方程是正确的。但是它包含：

• 需要求解一个整体的半球体积分，会有来自四面八方的光照
• 递归问题

那么我们该如何求解这个整体的积分？

蒙特卡罗求积分

1. 详细步骤：

PDF & PMF 概念与区别：

PDF：对连续性随机变量的定义。与PMF不同的是PDF在特定点上的值并不是该点的概率, 连续随机概率事件只能求一段区域内发生事件的概率, 通过对这段区间进行积分来求。

PMF：对离散随机变量的定义。是离散随机变量 在各个特定取值的概率。

2. 一般式

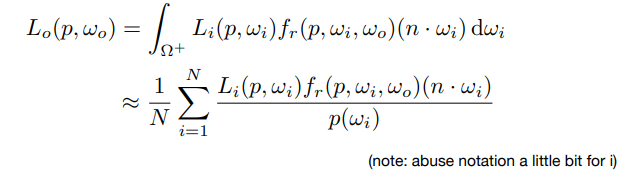
（三）全局光照

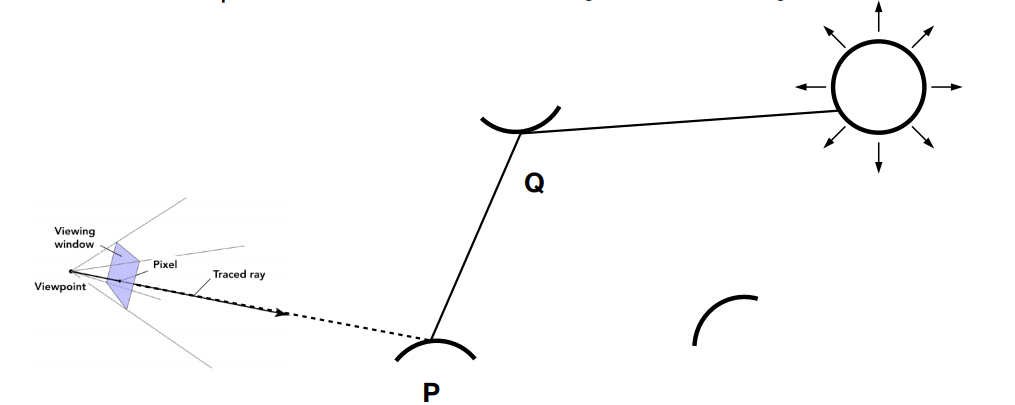
对上图，主要有以下问题：

1. 路径追踪——Explosion of #rays as #bounces go up:

如果对每一条路径进行追踪，那么不断经过漫反射后计算会爆炸。示意图如下：