图形学之图像信号处理
图像信号处理在图形学中有举足轻重的作用,这节博客对图像的采样、滤波和重构进行简要总结。
一、离散图像滤波
图像中最广泛的应用是使用简单的卷积滤波器。通过与一般的低通滤波器(从盒式滤波器到高斯滤波器)进行卷积,实现对图像的模糊化处理。例如下图中高斯模糊看起来很平滑,被广泛使用。

二、反走样技术
在图像合成中,对于连续数学公式表示的图像,常常需要产生一幅对应的采样图像(例如:光线追踪)。
对于连续的二维信号(图像),需要基于规则的二维点阵进行采样,否则容易出现各种走样情况。例如下图效果:

走样原因是图像中包含很多小尺度特征。在采样之前,需要滤波去掉这些特征。例如:盒式滤波器会改善突变边缘,但是仍会产生莫尔图案;高斯滤波抑制莫尔效果较好,但是会使图像整体偏向模糊。例如下图:

三、重构与重采样
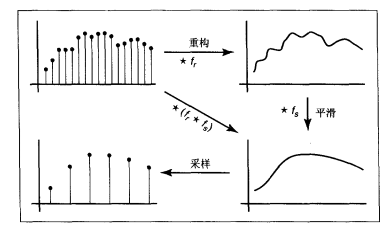
当对滤波要求较高时,重采样是常见的图像运算之一。重采样就是改变图像大小。
高像素调整为低像素显示的两种方法:
- 看作是删除像素。在留下的像素之间去掉一个或者两个像素。可以实现压缩图像的目的,但是图像质量变低。
- 对图像重采样。首先根据输入样本重构一个连续函数,然后对函数进行采样。为了避免走样,在每一步均要选择合适的滤波器。
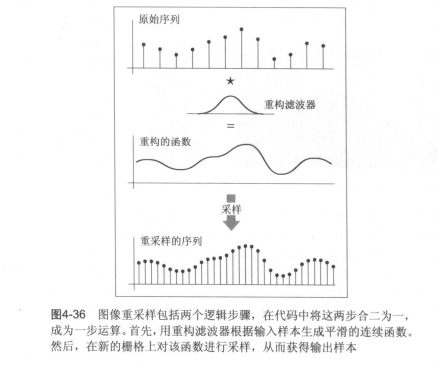
例如下图示例,原始图像为\(12 \times 9\)像素,而新图像是\(8 \times 6\)像素。在每一维,输出像素数是输入像素数的 2/3,因此图像上的像素间隔是原始图像的 3/2。

’空心黑圈‘ 为输入样本点,’实心黑点‘ 为输出样本点。
为了给每个输出样本赋值,需要计算样本之间的图像值。像素删除方法提供方法:取输入图像中与样本最近的值作为输出值(等价“用一个像素宽的盒式滤波器重构图像,再进行点采样”)。
重采样包括:重构滤波和采样滤波。因为序列中的两卷积滤波可以用单一的滤波器来代替,因此只需要重采样滤波器(同时起到重构和采样的作用)。